摘要 本文进行了有关钢在马氏体淬火过程中应力与相变相互作用的实验研究,在此基础上提出了一种预测钢的马氏体淬火残余应力的较完整的数学模型。根据实测的材料参数用有限元方法对26Cr2Ni4MoV钢圆筒形试件的淬火过程进行了计算分析,着重考察了相变塑性和应力诱导相变对残余应力形成的影响。结果表明,由本模型给出的残余应力预测值与实测值吻合较好,而不考虑相变塑性的模型实际上是不适用的,忽略应力诱导相变则倾向于在较大程度上低估淬火后的残余应力。
关键词 马氏体淬火残余应力 相变塑性应力诱导相变 数值模拟
1 前言
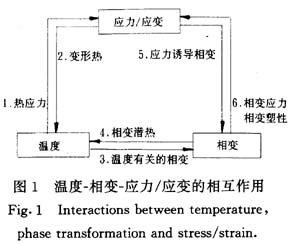
钢在淬火过程中存在极为复杂的温度、相变、应力/应变相互作用,在此方面已有许多报道[1]。如图1所示,在淬火过程中,温度造成热应力并影响材料的力学参数(弹性模量、泊松比、屈服强度和应变硬化率等),从而影响材料的力学行为。应力/应变则以变形热的形式反过来影响温度的变化。随着温度的降低,在达到相变条件后将发生相变。温度是决定相变的因素之一,但其本身又受着相变潜热的影响。内应力的存在,可通过一种通常称为应力诱导相变的机制而影响相变的进程。在相变过程中,各组成相的比容差异将造成相变应力,同时由于材料的绝大多数参数除了依赖于温度实际上也依赖于相态,因此,相变也会对材料的力学行为产生影响。此外,在有内应力存在时相变过程中还会伴随一种“反常”的塑性行为,即材料在应力低于屈服强度的情况下就可以发生不可逆变形的现象,称为相变塑性。
完整的数值计算模型包括上述相互作用的各个方面,但由于淬火过程中变形热的影响很小,所以几乎所有研究者都忽略了该因素的影响。在其余的相互作用中,就目前所研究到的现象或机制来看,除了相变塑性和应力诱导相变外,在数值模拟方面均已比较成熟。数值模拟技术要求在可靠的试验数据基础上建立准确的数学模型,即要求较准确的定量化。从这个角度看,目前对于相变塑性和应力诱导相变的研究,不论是在数据积累、数学模型的建立,还是在测试方法乃至机理方面,都是不成熟的。本文基于这些考虑,着重进行了有关应力与相变相互作用的实验研究,并在此基础上提出了一种预测钢的马氏体淬火残余应力的较完整的数学模型。根据该模型,用有限元方法对26Cr2Ni4MoV钢圆筒形试件的马氏体淬火过程进行了计算。重点考察了相变塑性和应力诱导相变对残余应力形成的影响,并验证了数学模型的适用性和准确性。
2 应力与相变相互作用的实验研究
我们对26Cr2Ni4MoV转子钢在淬火过程中的应力与相变相互作用进行了实验研究,主要目的是实测应力对相变动力学的影响和相变塑性规律,同时也可以获取数值模拟过程中所需的其它一些参数,如温度膨胀系数、组织转变膨胀系数等。
实验采用连续冷却方式,在Gleeble-1500热-力学模拟试验机上进行。试样为φ10×130标准试样,在其中部焊有CrNi-CrSi热电偶以测量和控制温度,同时在该部位放置高温夹式引伸计。实验时抽真空至5×10-4乇后,将试样加热至860℃,保温10min以充分奥氏体化。对加载实验,随后以15℃/s急冷至Ms点(本钢约为325℃)以上50~80℃,接着在5s内加到所需的单轴应力水平。然后将冷速改为4℃/s,并一直保持该载荷和冷速至室温。整个过程中用自动记录仪记录试样直径变化与时间的关系曲线。应力水平取0MPa、±60MPa、±120MPa和±180MPa,均低于材料400℃时的奥氏体屈服极限(约200MPa),以便于相变塑性研究。
实验数据处理过程中均采用最常用的关系式。对马氏体转变,在没有应力作用时,通常采用如下所示的Koistinen-Marburger公式