轴向长度上、工作转速高的转子,转动时在不平衡质量作用下会沿轴向产生弯矩,发生弹性变形,不能采用不计轴线弯曲变形的刚性转子动平衡方法。理论上如果能找到原始不平衡量的数值和相位,即可以在其对称位置加上一个相等的平衡质量,消除轴承的动反力及沿轴向的弯矩。实际上转子沿轴向的不平衡质量的分布难以确定,一般只能采用挠性转子高速动平衡工艺,使转子在一定转速下的轴承反力和弯矩值为最小。
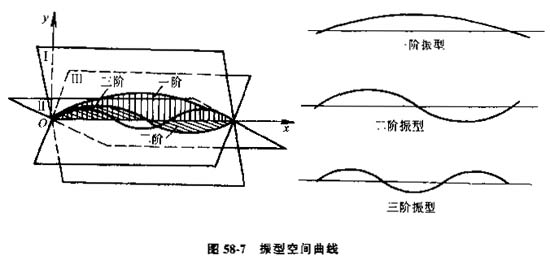
(1)挠性转子动平衡原理,将挠性转子简化为一根简支梁,梁在其弹性稳定平衡位置附近会发生多种形式的微小振动,其中横向振动是挠性转子动平衡的理论基础,整个转子的振动位移,即动挠度曲线上一条绕如图58-7所示的转轴Oz,以角速度w回转的空间曲线,可以视该曲线为无限多条固有频率不同的振型曲线在空间叠加而成。各阶振型曲线所在平面互不重合,图58-7所示为三个振型的空间曲线。
当转速变化时,各阶振型曲线的幅值及所占的比例均随转速变化,从而动挠度曲线也随转速变化。当转速接近某阶临界转速时,动挠度曲线形成相应的某阶振型曲线。不平衡质量的某阶振分量只能激发与之相应的那一阶挠度振型分量,不能激发其他阶的振型分量,称为振型函数的正交性。
挠性转子的动平衡同样包括平衡检测和平衡校正两个内容。平衡检测是将转子驱动至一定的转速,通过对轴承振动或转子动挠度的测量,以求知引起轴承动反力或转子动挠度的原始不平衡质量的大小和分布规律。实用中转子动挠度不易测量,多为测量轴承振动。轴承振动往往是转子加上测量系统各部件及周围环境各种机械振动的综合反应,因此,在平衡检测时,要求能正确检测出由转子不平衡引起的那部分振动,检测仪器应具有选频滤波能力和足够的精度,并使平衡转速保持稳定和具有复现能力。
转子原始不平衡量沿轴方向的分布为一条空间曲线,难以直接测量,因此通常在转子上加一个或几个试加质量,然后分别测量转子在试加质量前后因不平衡量的变化而引起的轴承振动的变化,再计算出原始不平衡量的大小和分布规律。转子的校正总是用两个或两个以上的集中质量,而不是用分布式的校正质量。确定平衡校正面的数目及其轴向位置是挠性转子动平衡的关键。
图58-7 振型空间曲线