6.3齿向载荷分布系数KHβ,KFβ
6.3.1KHβ的定义及影响因素
齿向载荷分布系数KHβ是考虑沿齿宽方向载荷分布不均匀对齿面接触应力影响的系数,其定义为:
式中:ωmax——单位齿宽最大载荷,N/mm;
ωm——单位齿宽平均载荷,N/mm;
Fm——分度圆上平均计算切向力,N;Fm=FtKAKV。
式中:b——齿宽,mm;对人字齿轮或双斜齿轮,应取两个斜齿轮宽度之和。影响齿向载荷分布的主要因素有:
a)齿轮副的接触精度(GB 10095–88 第Ⅲ公差组精度),它主要取决于齿轮加工误差、箱体镗孔偏差、轴承的间隙和误差、大小轮轴的平行度、跑合情况等;
b)轮齿啮合刚度、齿轮的尺寸结构及支承型式及轮缘、轴、箱体及机座的刚度;
c)轮齿、轴、轴承的变形,热膨胀和热变形(这对高速宽齿轮尤其重要);
d)切向、轴向载荷及轴上的附加载荷(例如带或链传动);
e)设计中有无元件变形补偿措施(例如齿向修形)。
由于影响因素众多,确切的载荷分布系数应通过实际的精密测量和全面分析已知的各影响因素的量值综合确定。这时,要论证应用方法的精确度和可靠性,并明确其前提条件。这种方法特别适用于调质小齿轮宽径比b/d>1.5或硬齿面小齿轮b/d>1.2的重要齿轮装置的校核计算。
各影响因素引起轮齿沿齿宽的综合变形、位移和制造误差的合成量称初始啮合齿向误差(跑合前轮齿啮合齿向误差)以表示Fβx表示。它是决定齿向载荷分布系数的重要数据。在通过实测或综合的精确计算得到初始啮合齿向误差Fβx时,可按式(56)至式(60)求得齿向载荷分布系数KHβ值。
当按上述方法得到的啮合齿向误差由齿向修形补偿的高精度齿轮副,在给定的运行条件下,其齿向载荷接近均匀分布,KHβ接近于1。
在无法按上述方法确定KHβ时,可按本标准提供的下述两种方法——一般方法或简化方法近似计算齿向载荷分布系数。
6.3.2KHβ计算的一般方法
KHβ计算的一般方法适用条件列于6.3.2.1,计算公式按6.3.2.2。对于符合6.3.2.7中条件的一些典型结构齿轮装置,如单对齿轮、轧机齿、简单行星齿轮,其可KHβ按6.3.2.7所列公式计算。
6.3.2.1基本假定和适用范围
a)沿齿宽将轮齿视为具有啮合刚度CY的弹性体,载荷和变形都呈线性分布(参见图4);
b)轴齿轮的扭转变形按载荷 沿齿宽均布计算,弯曲变形按载荷集中作用于齿宽中点计算,没有其他额外的附加载荷;
c)箱体、轴承、大齿轮及其轴的刚度足够大,其变形可忽略;
d)等直径轴或阶梯轴, dsh为与实际轴产生同样弯曲变形量的当量轴径;
e)轴和小齿轮的材料都为钢;小齿轮轴可以是实心轴或空心轴(其内径应﹤0.5dsh)齿轮的结构支承形式见图5,偏心距s/l≤0.3。
6.3.2.2KHβ的计算公式
KHβ可用式(57)或式(59)计算
采用说明:
4]ISO 6336原判别式为bca1/b在设计时为未知,故改用此判别式。
上述各式中:bca1——计算齿宽,见图4;
Cy——轮齿啮合刚度,见6.5;
Fβy——跑合后啮合齿向误差,μm;
ωm——计算见式(55)。
Fβy=Fβx-yβ=Fβxxβ…………………………………………(60)
式中:Fβx——初始啮合齿向误差,μm,见6.3.2.3;
yβ——齿向跑合量,μm,见6.3.2.6;
Xβ——齿向跑合系数,见6.3.2.6.
当KHβ>1.5时,通常应采取措施降低KHβ值。
|
K′ |
图号 |
结构示图 |
|
刚性 |
非刚性 |
|
0.48 |
0.8 |
a) |
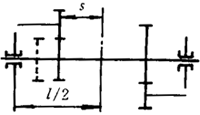 s/l<0.3 |
|
-0.48 |
-0.8 |
b) |
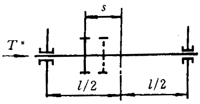 s/l<0.3 |
|
1.33 |
1.33 |
c) |
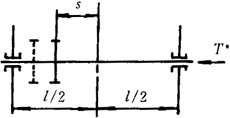 s/l<0.5 |
|
-0.36 |
-0.6 |
d) |
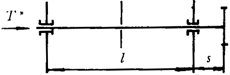 s/l<0.3 |
|
-0.6 |
-1.0 |
e) |
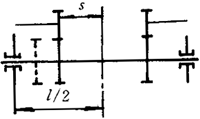 s/l<0.3 |
注
1 对人字齿轮或双斜齿轮,图中实、虚线各代表半边斜齿轮中点的位置,S按用实线表示的变形大的半边斜齿轮的位置计算,b取单个斜齿轮宽度。
2 图中,d1/dsh ≥1.15为刚性轴,d1/dsh <1.15为非刚性轴。通常采用键联接的套装齿轮都属非刚性轴。
3 齿轮位于轴承跨距中心时(S≈0),最好按6.3.2.7的公式计算。
4 当采用图5以外的结构布置型式或s/l超过图5规定的范围,或轴上作用有皮带轮或链轮之类的附加载荷时,推荐进一步的分析。
6.3.2.3初始啮合向误差KHβ
可据KHβ可据不同情况分别按式(61)~(63)计算。
a)在载荷作用下没达到全齿宽接触或未能验证有良好的接触长度和位置时
Fβx=1.33fah+fma; Fβx≥Fβxmin………………………………………………(61)
b)当已证实达到所希望的接触斑点时(例如彩齿向修形或装配时调整、对研、部分加载跑合、精确计算鼓形量或齿端修薄量等方法,使弹性变形和制造误差相互补偿)
Fβx=|1.33fah-fma|; Fβx≥Fβxmin……………………………………………(62)5]
c)在载荷作用下达到理想的接触斑点时
Fβx=Fβxmin……………………………………………(63)
上述各式中:Fβxmin=max{(0.005mm·μm /N)ωm,0.5Fβ}……………………………(64)
即Fβxmin取0.005ωmt 0.5 Fβ二者中之大值。μm;
fsh——综合变形产生的啮合齿向误差分量,μm,见6.3.2.4;
fma——制造、安装误差产生的啮合齿向误差分量,Um,见6.3.2.5;
Fβ——齿向误差,μm;
Fβ6——GB10095-88的6级精度的齿向公差Fβ,μm.
6.3.2.4综合变形产生的啮合齿向误差分量fsh
fsh——是考虑小齿轮和小齿轮轴的弯曲和扭转变形产生的啮合齿合误差。
当fsh无法实测或精确计算时,要按下式确定:
fsh=ωmfsho=(Fm/b)fsho………………………………………………(65)
式中fsh——载荷作用下的的啮合齿向误差,μm;
fsho——单位载荷作用下的啮合齿向误差,μm·mm/N;可按表7中的公式计算。
表7 fsho计算公式
|
齿轮型式 |
fsho计算公式 |
|
一般齿轮 |
0.023y (66) |
|
齿端修薄的齿轮 |
0.016y (67) |
|
修形或鼓形修整的齿轮 |
0.012y (68) |
表中:γ——小齿轮结构尺寸系数,可根据图5先取系数K′值后,按表8中的公式计算。
表8 小齿轮结构尺寸系数y
采用说明:
5] 式(62)是ISO6336新增的,因含有|1.33fsh-fβ6|项,使用时需加限制条件(如精度及b/d值),否则将出现明显不合理的结果。
6.3.2.5 制造、安装误差产生的啮合齿向误差分量fma
fma的大小取决于齿轮副加工的齿向误差与轴线间平行度的组合(彼此叠加或补偿)以及是否进行装配调整。
如无实测数据,fma可按表9中的方法之一确定。
表9fma计算公式(μm)
|
类别 |
确定方法或公式 |
|
粗略数值 |
某些高精度的高速齿轮 |
fma=0 |
|
一般工业齿轮 |
fma=15μm |
|
给定精度等级 |
装配时无检验调整 |
fma=1.0Fβ |
|
装配时进行检验调整(对研,轻载跑合,调整轴承,螺旋线修形,鼓形齿等) |
fma=0.5Fβ |
|
齿端修薄 |
fma=0.7Fβ |
|
给定空载下接触斑点长度bco |
fma=(b/bc0)Sc (71)
SC——涂色层厚度,一般为2~20μm,
计算时可取
SC=6μm
如按最小接触斑点长度bcomin计算
fma=2/3(b/bc0min)Sc (72)
如测得最长和最短的接触点长度
fma=1/2(b/bc0min+b/bc0max)Sc (73) |
6.3.2.6 齿向跑合量yβ,跑合系数Xβ
齿向跑合量yβ是考虑跑合后使啮合齿向误差减小的量,um; Xβ是表示跑合啮合齿向误差Fβy的比例数据,yβ,Xβ可用表10中各式计算。
表10 yβ、xβ计算公式
|
齿轮材料 |
齿向跑合量yβ,um,跑合系数Xβ |
适用范围及限制条件 |
|
结构钢、调质
钢、珠光体或
贝氏体球墨铸铁 |
yβ=320/σHlimFβx
(74)
xβ=1-320/σHlim |
V>10m/s时,
yβ≤12800/σHlim FβX≤40μm;
5<v≤10m/s时,
yβ≤25600/σHlim
FβX≤80μm;
v≤5m/s时,
yβ无限制 |
|
灰铸铁、铁素
体球墨铸铁 |
yβ=0.55Fβx
(75)
xβ=0.45 |
V>10m/s时,
yβ≤22μm, FβX≤40μm;
5<v≤10m/s时,
yβ≤45μm, FβX≤80μm;
v≤5m/s时,
yβ无限制 |
|
渗碳淬火钢、表面硬化钢、氮化钢、
氮碳共渗钢、表面硬化球墨铸铁 |
yβ=0.15Fβx
(76)
xβ=0.85 |
yβ≤6um. FβX≤40um |
|
注
1σhlim——齿轮接触疲劳限值,N/mm2,见8.1.2
2 当大小齿轮材料不同时,yβ=(yβ1+ yβ2)/2,Xβ=(Xβ7=+Xβ2)/2,式中下标1,2分别表示大、小齿轮。 |
6.3.2.7 典型结构齿轮的FβX
a)适用条件
1)沿齿宽将齿轮视为具有啮合刚度cy的弹性体,载荷和变形均呈线性分布;
2)在载荷作用下接触斑点布满全齿宽,轴齿轮的扭转和弯曲变形均按载荷沿齿宽均布计算,没有其他额外的附加载荷;
3)小齿轮直径和轴径相近,轴齿轮为实心或空心轴(内孔径应<0.5dsh),对称布置在两轴承之间(s/l≈0);非对称布置时,应把估算出的附加弯曲变形量加到fma上;
4)箱体、轴承、大齿轮及其轴的刚度足够大,其变形可忽略。
符合上述条件的单对齿轮、轧机齿轮和简单行星传动可按下述b)~d)中的公式计算KHβ。
b)单对齿轮
符合a)中条件的单对齿轮,可按表11中的公式计算KHβ。
表11 单对齿轮的KHβ计算公式
c)轧机齿轮
轧机齿轮机座采用一对轴齿轮,u=1,功率分流,被动齿轮传递k%的转矩、另外(100-K)%有转矩由主动齿轮的轴端输出,两齿轮皆对称布置在两端的轴承之间,其KHβ值可按表12中公式计算。
表12 轧机齿轮的KHβ计算公式
d)简单行星传动齿轮
符合项a)中条件的行星传动中的各齿轮副:太阳轮(S)/行星轮(P)、内齿轮(H)/行星轮,其KHβ可按表13中的公式计算。计算时应取
式中:ωm——单位齿宽平均载荷,N/mm;
Ky——不均载系数;
Np——行星轮个数。
表13 行星传动齿轮的KHβ计算公式
注
1 Ⅰ,Ⅱ表示行星轮及其轴承在行星架上的安装型式:Ⅰ——轴承装在行星轮上,转轴刚性固定在行星架上;Ⅱ——行星轮两端带轴颈的轴齿轮,轴承装在转架上。
2 ds——太阳轮分度圆直径,mmdp——行星轮分度圆直径,mm;;lp——行星轮轴承跨距,mm;B为包括空刀槽在内的双斜齿宽度,mm;bB为单斜齿轮宽度,mm。
6.3.3 KHβ计算的简化方法
6.3.3.1适用范围
a)中等或较重载荷工况:对调质齿轮,单位齿宽载荷Fm/b为400~1000N/mm;对硬齿面齿轮,Fm/b为800~1500N/mm。
b)刚性结构和刚性支承,受载时两轴承变形较小可忽略:齿宽偏置度s/l较小,符合表14、表15限定范围。
c)齿宽b为50~400mm,齿宽与齿高比b/h为3~12,小齿轮宽径比b/d1对调质的应小于2.0,对硬齿面的应小于1.5。
d)轮齿啮合刚度cy为15~25N/(mm·μm)。
e)齿轮制造精度对调质齿轮为5~8级,对硬齿面齿轮为5~6级;满载时齿宽全长或接近全长接触(一般情况下未经齿向修形)。
f)矿物油润滑。
6.3.3.2计算公式
齿轮第Ⅲ公差组精度为5~8级(硬齿面为5~6级)及相应的结构布局限制条件的KHβ简化计算公式见表14或表15。
表14 调质齿轮KHβ的简化计算公式
表15 硬齿面齿轮KHβ的简化计算公式
6.3.4 KFβ的计算公式
齿向载荷分布系数KFβ是考虑沿齿宽载荷分布对齿根弯曲应力的影响。对于所有的实际应用范围,KFβ可按下式计算:
KFβ=(KHβ)N……………………………………………(139)
式中:KHβ——接触强度计算的齿向载荷分布系数,见6.3.2或6.3.3;
N——幂指数。
式中:b——齿宽,mm,对人字齿或双斜齿齿轮,用单个斜齿轮的齿宽;
H——齿高,mm。
b/h应取大小齿轮中的小值。
图6给了按式(139)、(140)确定的近似解。
图6 弯曲强度计算的齿向载荷分布系数KFβ