6计算
6.1圆柱齿轮
GB/Z6413的本部分含有能评定用油润滑的渐开线直齿和斜齿齿轮的“胶合概率”(热胶合)的有关公式。
假定整个切向载荷在双斜齿轮的两条螺旋线之间是等量分布的。当由于有像外部轴向力这样的力的作用时,则不属于这种情况,这些力的影响必须分别考虑进去,这两条螺旋线应按平行的单斜齿轮来处理。包括影响胶合概率的各种因素可做出定量的评定。
这些公式对于具有与GB/T1356规定的基本齿条相啮的外齿或内齿齿轮均适用。对于内啮合齿轮,在确定6.1.10给出的几何系数XBE时,必须引入负值。它们也可考虑适用于端面重合度为εα≤2.5的符合其他基本齿条的类似齿轮。
6.1.1 胶合承载能力计算的安全系数SintS
当假设中的不确定性与不精确度不能排除时,有必要引入安全系数SintS。必须指出胶合承载能力计算的安全系数与温度有关,而不是这样一个系数,即用它乘以齿轮的转矩,使积分温度Θint与胶合积分温度ΘintS达到相同的数值。
Ssmin的选用建议
Ssmin<1,高胶合危险。
1≤Ssmin≤2,具有中等胶合危险的临界范围,受实际齿轮工作条件的影响。影响因数有例如齿面粗糙度、跑合效果、载荷系数的准确理解、润滑油的承载能力等。
Ssmin>2,低胶合危险。
为给出实际载荷与积分温度数之间的关系,相应的载荷安全系数SS1可近似由下式取得:
6.1.2许用积分温度ΘintP
要求的最小胶合安全系数 对每种应用情况应分别确定。
6.1.3积分温度
Θint=ΘM+C2·Θflaint≤ΘintP……………………(17)
式中:
C2——由实验得出的加权系数,对于直齿与斜齿齿轮,C2=1.5。
Θflaint=ΘflaE·XE………………(18)
6.1.4小齿轮顶的闪温ΘflaE
6.1.5本体温度ΘM
本体温度是即将进入啮合时的齿面温度。
本体温度是通过齿轮箱的热平衡过程而建立起来的。在齿轮箱中,有几中热源,其中最重要的是轮齿、轴承的摩擦。其他的热源例如密封与油流在某种程度上也是其中之一。当节线速度超过80m/s时,在啮合和风阴损失中因搅油而产生的热是重要的。应予以考虑(见方法A)。该热量经过传导、对流与辐射,再经箱体而传递到周围环境,对于喷油润滑,则通过油进入外部的热交换器。
用以下不同计算方法得到的数值须用下标A、B、C加以区别。
6.1.5.1 A法ΘM-A
本体温度作为平均值或作为齿宽上的温度分布可用实验测定或采用基于已知功率损失与传热数据进行理论分析确定,即采用热网格方法确定。
6.1.5.2 B法ΘM-B
此法不用于积分温度法(见GB/Z 6413.1中给出的闪温法)。
6.1.5.3C法ΘM-A
本体温度的近似值由油温加上沿啮合线上得出的闪温平均值的(根据方法C)一部分之和来确定。
ΘM-C=Θoil+C1·Xmp·Θflaint·XS………………(20)
式中:
对于喷油润滑:XS=1.2;
对于油浴润滑:XS=1.0;
对于将齿轮浸没油中:XS=0.2;
C1——考虑了热转换条件的常数,试验结果为:C1=0.7;
式中:np——同时啮合的齿轮的数量。
6.1.6平均磨擦因数μmc
见5.1。
6.1.7跑合系数XE
见5.2
6.1.8热闪系数XM
见5.3。
6.1.9压力角系数Xαβ
见5.4。
6.1.10小轮齿顶的几何系数XBE
几何系数XBE考虑小轮齿顶的赫兹应力与滑动速度的影响。XBE是齿数比u与小轮齿顶E点处曲率半径ρE的函数。
对于内啮合齿轮,下面的参数必须用负值代入:齿数 、齿数比u、中心距α以及所有直径。
6.1.11 啮入系数XQ
啮入系数XQ考虑了在高滑动区域,在正进入啮合处(在被驱动齿轮的齿顶处)的冲击载荷。可用啮入重合度εf与 与啮合重合度εa之比的函数来表示,见图3。
图3啮入系数XQ
当齿顶被倒棱或倒圆时,顶圆直径da必须用啮出开始点的有效顶圆直径dNa来替代。
6.1.12 当顶修缘系数XCa
受载轮齿的弹性变形在滑动较大的齿顶处会产生高的冲击载荷。齿顶修缘系数XCa考虑了齿廓修形对这种载荷的影响。XCa是一个相对的齿顶修缘系数,它取决于相对于因弹性变形引起的有效齿顶修缘量Ceff的齿顶修缘量Ca,见图4。
图4的曲线可能用公式(32)近似确定。
式中:
εmax——ε1或ε2中的最大值。
图4 由实验数据[8,9]得出的齿顶修缘系数XCa
被引入到公式(32)的齿顶修缘的名义量Ca取决于齿顶修缘的实际值Ca1、Ca2有效齿顶修缘量Ceff、齿顶重合度的比值及功率流的方向。
当小轮驱动大轮且ε
1>1.5ε
2或大轮驱动小轮且
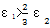
时:
对于Ca1 Ceff Ca= Ca1…………………………………………………(33)
对于Ca1> Ceff Ca= Ceff …………………………………………………(34)
当小轮驱动大轮且ε
1≤1.5ε
2或大轮驱动小轮且
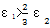
时:
对于Ca2≤Ceff Ca= Ca2…………………………………………(35)
对于Ca2>Ceff Ca= Ceff ……………………………………………(36)
Ceff——有效齿顶修缘量,用以补偿单对齿啮合时轮齿的弹性变形。
对于直齿轮
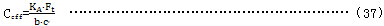
对于斜齿轮
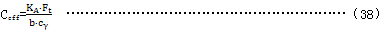
式中:
b——齿宽,当大、小轮的齿宽不同时,取其中较小值。
上述的齿顶修缘量适量于GB/T10095.1中6级或更好的齿轮。对于低精度齿轮,规定XCa=1,也可参见GB/T3480。
6.1.13重合度系数Kε
重合度系数Kε是考虑在忽略载荷分配时,将小轮齿顶的闪温值转换为沿啮合线闪温平均值的系数。重合度系数可以用齿高重合度ε1与ε2以及它们的和εa来表示。Xε的公式是基于假定沿啮合线的闪温是线性分布的。这种方法的可能误差将不会超过5%,且偏于安全。
图5 1≤εa<2时的载荷与温度分布
对于2≤εa<3,ε1≥ε2(见图6)
图6 2≤εa<3时的载荷与温度分布
6.2锥齿轮
本条是6.1所述积分温度法的继续。
计算时,用锥齿轮中点直径确定的当量圆柱齿轮来近似锥齿轮(当量圆柱齿轮的计算见GB/T10062.1)。为此,GB/Z 6413 的本部分规定的计算方法的结构与圆柱齿轮的内容相当。
对于替代锥齿轮的当量圆柱齿轮(按锥齿轮端面内中点直径确定)的胶合承载能力,按6.1计算。
6.2.1胶合承载能力计算的安全系数SintS
见6.1.1。
6.2.2许用积分温度ΘintP
见6.1.2。
6.2.3积分温度Θint
见6.1.3。
对于当量圆柱齿轮,C2=1.5。
6.2.4小轮齿顶的闪温ΘflaE
见6.1.4并采用下列替换:
——在公式(19)中:用aV代替a,vmt代替v;
——在公式(4)中:有Fmt代替Ft,beB代替b。
有效齿宽beB考虑了锥齿轮的鼓形。
beB=0.85b2
式中:
b2——小轮与大轮的公用齿宽。
系数KA、KV、KBβ= KHβ以及KBα= KHα应按GB/T10062.1确定。
KBγ= 1
6.2.5本体温度ΘM
见6.1.5。
6.2.6平均磨擦因数μmc
见5.1,并采用下列替换:
——在公式(4)中:用Fmt代替Ft,beB代替b。
对于一般锥齿轮设计情况αt=αvt,即x1=x2:
vΕC=2·vmt·sinαvt………………………………………(47)
KBγ=1
6.2.7跑合系数XE
见5.2。
6.2.8热闪系数XM
见5.3。
6.2.9压力角系数Xαβ
6.2.9.1 A法:系数Xαβ-A
对于一般锥齿轮设计的情况α′t=αvt,即x1=-x2:
6.2.9.2 B法:系数Xαβ-B
见5.4。
6 .2.10小轮齿顶的几何系数XBE
见6.1.10,并采用下列替换:
——在公式(22)中:用uv代替u;
——在公式(23)中:用dval代替da1,dab1代替db1;
——在公式(24):αvt代替α′t。
6.2.11啮入系数XQ
见6.1.11,并采用下列替换。
——在公式(28)~公式(31)中:用εv1代替εv2,εv2代替ε2;
——在公式(30)与公式(31)中:用dva1,2代替da1,2,dvb1,2代替db1,2,αvt代替α′t,zv1,2代替z1,2。
6.2.12齿顶修缘系数XCa
在6.1.12,并采用下列替换:
——在公式(32)中,用εvmax代替εmax,εvmax是εv1或εv2中的量大值。
假定齿顶与齿根的修缘量被选为运行条件下的量佳值(满负荷接触斑点刚好扩展到齿顶而没有聚集现象),于是应用以下的近似方法:
6.2.13重合度系数Xε
见6.1.13,并在公式(39)~公式(45)中及其有效的条件下,采用下列替换:
用εva代替εa,εv1代替ε1εv2代替ε2。
6.3准双曲面齿轮
准双曲面齿轮胶合承载能力的计算方法是遵循6.1圆柱齿轮积分温度准则。
为计算胶合承载能力,将准双曲面齿轮当作具有与实际准双曲面齿轮同样滑动条件的当量交错轴斜齿轮来近似处理(6.3.11当量交错轴斜齿轮副)。
6.3.1胶合承载能力计算的安全系数SintS
见6.1.1。
6.3.2许用积分温度ΘintP
见6.1.2。
6.3.3积分温度Θint
见6.1.3,并采用下列替换:
——在公式(17)中:用C2H代替C2(按照试验结果,C2H=1.8),Θflainlh代替Θflainl。
KBβbe=KHβbe………………………………………………(52)
KBβbe=KHβbe(见GB/T10062.1)
6.3.4本体温度ΘM
见6.1.5。
6.3.5平均磨擦因数μmc
见5.1,并采用下列替换:
——在公式(1)中:用ρCn代替ρredC;
——在公式(4)中:用beB/cosβb2代替b,Fn代替Ft;
beB;见公式(46)。
KBγ=1
KBγ·KBα=2.0(仅为计算μmc时的近似值)………………(53)
XR:见公式(7),并使用ρCn代替ρredC。
6.3.6跑合系数XE
见5.2,并在公式(8)中采用下列替换:
——用ρCn代替ρredC。
6.3.7 几何系数XG
几何系数XG是考虑平均赫兹应力与沿啮合线的平均啮合长度影响的系数。作为一种近似方法,它可利用节点处的数值来确定(ρCn,L)。
图7作为cosθ的函数的辅助系数
6.3.8啮入系数XQ
见6.1.11,并采用下列替换:
——在公式(28)~公式(31)中:用εn1代替ε1,εn2代替ε2。
6.3.9齿顶修缘系数XCa
见6.1.12,并采用下列替换:
——在公式(32)中,用εnmax代替εmax,εnmax为εn1或εn2中的最大值。
为获得适当的齿顶与齿根的修缘:
Ca/Ceff=1,见6.2.12。
6.3.10重合度系数Xε
对于啮出线长度大致相同的(gan1≈gan2)齿轮副,滑动系数g*接近等于1。
6.3.11当量交错轴斜齿轮的计算
这一部分包含了准双曲面齿轮副转换成交错轴斜齿轮副的几何关系,将准双曲面齿轮的齿宽中点处的条件作为转换的基础(见图8)。
当量交错轴斜齿轮的参数:
螺旋角
βs1,2=βm1,2………………………………………………(63)
法向压力角
αsn=αmn………………………………………………(64)
交错轴斜齿轮的交错角
Σ=βm1-βm2………………………………………………(65)
端面压力角
αst1,2
基圆螺旋角
分度圆直径
顶圆直径
da1,2=ds1,2=2ham1,2…………………………………………(69)
基圆直径
db1,2=ds1,2·cosαt1,2……………………………………(70)
交错轴斜齿轮的轴交角
tanβb1,2=tanβm1,2·sinαmm……………………………………(71)
φ=βb1+βb2………………………………………………(72)
模数
msn=mmn………………………………………………(73)
法面基圆齿轮
ρen=msn·π·codαmm………………………………………(74)
法截面上的曲率半径
图8 当量交错轴斜齿轮的计算
切线速度
节点处切线速度之和
γ1,2=srctanγ1,2=arc(sinαsn·tanβs1,2)………………………………(86)
vgα1=vg1·cosγ1+vg2·cosγ2……………………………………(87)
vgβ1=vgs+vg1·sinγ1-vg2·sinγ2……………………………………(88)
齿合线长度
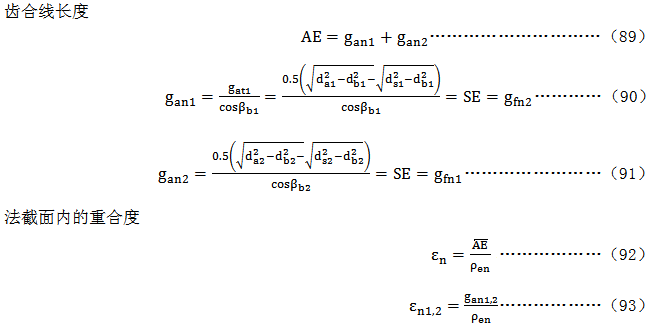
6.4胶合积分温度
胶合积分温度是产生胶合的温度根限值,它可以在试验结果的基础上进行计算。
此法适用于所在类型的油品(纯矿物油、EP油、合成油)。对于这些油的胶合承载能力已经通过试验齿轮确定(适用的试验例如有FZG-试验A/8.3/90、FZG L-42试验,Ryder齿轮油试验,或IAE齿轮油试验),或用实际的损伤情况来确定。
当试验齿轮的材料与相应的热处理与实际齿轮不致时,必须修正胶合温度,因为极限温度是材料——油品系统的函数。
6.4.1胶合积分温度Θints
根据积分温度的设定,当平均齿轮温度超出称之为胶合积分温度的值时,齿轮有可能胶合,这个温度值假定为齿轮副的润滑油与齿轮材料的组合所特有的,而且是通过类似的润滑油与齿轮材料的组合试验来确定的。
胶合积分温度值可由将任何齿轮油的胶合,试验数据代入6.1、6.2、6.3中的公式得到。这样,胶合积分温度值对任一油品:纯粹的矿物油、EP油或合成油可以计算出来。
6.4.1.1胶合积分温度的计算
热处理或表面处理齿轮钢与矿物油组合,组合的近似胶合积分温度值可从其他的热处理或表面处理齿轮钢和同样的润滑油组合的结果中得出。
ΘintS=ΘMT+XWrelT·C2·ΘflaintT………………………………(94)
式中:
C2=1.5,由试验获得。
6.4.1.2由试验结果确定ΘMT、ΘflaintT
图9所示为几种矿物油,在按照DIN51354[2]的FZG-试验A/8.3/90、Ryder[3]或FZG-Ryder试验[4]以及FZGL-42试验[5]等条件下确定的胶合承载能力的曲线。
为用计算机计算,图9 图11的曲线可以近似地用下列公式表达:
a)对于FZG试验A/8.3/90:
ΘMT=80+0.23·T1T·XL………………(95)
图9FZG试验A/8.3/90的胶合温度ΘintS
图10 Ryder与FZG-Ryder齿轮试验R/46.5/74E的胶合温度Θints
b)对于Ryder与FZG-Ryder试验R/46.7/71:
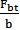
的单位为1b/in。
c)对于FZG L-42试验141/19.5/110:
6.4.2相对焊合系数XWrelT
相对焊合系数XWrelT是考虑热处理或表面处理对胶合积分温度影响的一个经验性系数。
式中:
对于FZG齿轮试验、Ryder齿轮试验以及FZG L-42试验,XWT=1;
XW——实际齿轮材料的焊合系数,见表3。
图11FZG L-42试验141/19.5/110的胶合Θints
表3焊合系数XW
|
齿轮材料 |
XW |
|
调质硬化钢 |
1.00 |
|
磷化钢 |
1.25 |
|
镀铜钢 |
1.50 |
|
液体与气体氮化钢 |
1.50 |
|
表面渗碳钢
平均奥氏体含量少于10%
平均奥氏体含水量量10%~20%
平均奥氏体含量大于20%~30% |
1.15
1.00
0.85 |
|
奥氏体钢(不锈钢) |
0.45 |