6齿距误差的检验

齿距误差的检验包括齿距偏差Δf_pt、齿距累积误差Δf_p和K个齿距累积误差Δf_pk的检验。

6.1测量方法和测量仪器

齿距误差的测量方法有相对法和绝对法。

相对法的测量仪器有万能测齿仪、半自动齿距仪、上置式齿距仪和旁置式齿距仪等。

绝对法的测量仪器有单面啮合整体误差测量仪、万能齿轮测量机等，也可在三坐标测量机、分度头和成能工具显微镜等仪器上测量。

6.1.1相对法测量原理

相对法测量原理参见图6。以被测齿轮回转轴线为基准（也可用齿顶圆代替），采用双测头2、4，以被测齿轮1上任一齿距或跨几个齿的齿距作为相对标准，通过传感器3依次测量各齿距或跨齿距的相对差值，按误差定义进行数据处理（见6.3.1），求得Δf_p、Δf_pk和Δf_pt。

图6 相对法测量原理

1—被测齿轮；2—测微测头；3—传感器；4—定位测头

6.1.2绝对法测量原理

绝对法又分为直接法和间接法。

直接法测量原理参见图7。以被测齿轮回转轴线为基准，用标准圆分度装置2（如圆光栅、分度盘等）对被测齿轮1分度，由测头4和传感器3测出齿距偏差。也可用测头4和传感器3定位，由标准圆分度装置测出实际齿距角，并装其与公称齿距角比较，其差值即为齿距偏差。按误差定义对测得值进行处理，求得Δf_p、Δf_pk和Δf_pt。

图7绝对法测量原理图

1—被测齿轮；2—标准圆分度装置；3—传感器；4—测头

间接法按16.1.1和16.1.2所述的测量原理先测出齿轮截面整体误差曲线，在该曲线上按误差定义取出Δf_p、Δf_pk、Δf_pt。

6.2测量

间接法测量见16.2。

6.2.1测量温度

见表1。

表1齿距误差的测量温度

被测齿轮精度等级	测量室室温度		被测齿轮与测量仪器(或测量元件)的温差
	相对法	绝对法	相对法	绝对法
3～5	20±2	20±3	≤2	≤3
6～7	20±3	20±5	≤3	≤4
≥8	20±5	20±8	≤4	≤5

6.2.2测量仪器的检定

仪器应按检定规程或其它有关技术文件的规定进行检定，经法定部门检定合格方准使用。

6.2.3测头的选择和调整

在保证不发生干涉和碰撞的情况下，宜选择直径较大的测头。

6.2.4测量基准的确定

见附录B（补充件）。

6.2.5测量位置的确定

齿距误差应在齿宽和齿高中部，对左、右侧齿面进行测量。对齿宽大于160mm的齿轮应至少测量上、中、下三个截面，上、下截面各距端面约百分之十五齿宽。单侧齿面工作的齿轮只测工作侧齿须。

用相对法测量齿数少于60的齿轮时，采用逐齿测量；测量齿数多于或等于60的齿轮时，对Δf_pt仍应采用逐齿测量，对ΔF_p和ΔF_pk一般应采用跨齿和逐齿补点测量，允许在保证测量不确定符合6.2.6规定的前提下，采用逐齿测量。

6.2.6测量的不确定度

齿距累积误差的测量不确定度UF_P、K个齿距累积误差的测量不确定度UF_PK和齿距偏差的测量不确定度Uf_Pt不应大于被测齿轮对应误差项目公差的三分之一。测量5级和高于5级精度的齿轮时，允许不大于二分之一，但此时应以五次以上重复测量结果的平均值作为测量结果。用测量法向齿距的方法测量斜齿轮时，UF_P、UF_PK和Uf_Pt不应大于五分之一；使用手提式仪器测量时UF_P、UF_PK和Uf_Pt不应大于五分之一。

当不能确定测量不确定度是否能满足上述要求时，应进行测量不确定度计算。

6.2.6.1齿距累积误差测量不确定度UF_P的计算

UF_P（μm）按下式计算：

式中：δ₁——仪器测量齿距累积误差时的示值误差[见附录A（补充件），也允许按仪器检定规程确定]，μm；

当被测齿轮齿数Z或跨齿测量的分组数Q大于仪器检定时所使用的标准齿轮齿数Z。时，还需用下式被充考核，下式中I为仪器的示值变动性：

δ₂——被测齿轮测量时的安装偏心引起的测量误差，μm；

δ₂=2e/cosα_t…………………………………………（26）

齿顶圆定位时，以顶圆跳动的一半作为安装偏心量。

6.2.6.2齿距偏差的测量不确定度Uf_pt的计算

Uf_pt（μm）按下式计算：

式中：δ₁——仪器测量齿距偏差时的示值误差[见附录A（补充件），也允许按仪器检定规程确定] μm；

      δ₂——被测齿轮测量时的安装偏心引起的测量误差，μm；

齿顶圆定位时，以顶圆跳动量的一半作为安装偏心量。

6.3测量结果处理

对齿距误差测量结果的处理可以采用计算法或作图法或误差曲线取值法（从整体误差曲线取值的方法见16.3.1）。

以在6.2.5所规定的各测量位置中测得的最大误差值作为测量结果。

Δf_p、Δf_pk、Δf_pt应在被测齿轮分度圆切线方向计值（μm），以其它方向测量时，应对测得值进行换算，见附录C（补充件）。

6.3.1相对法测量结果处理

6.3.1.1逐步测量

a.计算法

从逐齿测量数据计算f_p、Δf_pk和Δf_pt的方法列于表2，以Z=12、K=2的齿轮为例。

表2逐齿测量数据处理

△f_­pt=△P_i-△P_m=-5μm(取绝对值最大的偏差作为测量结果)………………（30）

△F_P=△F_­pimax-△F_pimin=10-(-7)=17μm…………………………（31）

△F_pk=△F_pkimax=8μm……………………………………（32）

b.作图法

直角坐标图上的X坐标代表齿序号i,Y坐标代表齿距误差（以公度圆弧长μm计值）。将测得值按齿序号i依次累积标在坐标图上（图8），过坐标原点和最后一个误差点作一直线，该直线即为计算△F_P、△F_PK、△f_pt的基准线，所有误差点相对基准线的Y坐标最大值和最小值之差为△F_P，相隔K个齿距的二个误差相对基准线的Y坐标最大差值为△F_PK，相邻两个误差点相对基准的Y坐标最大差值为△f_pt

图8逐齿测量结果处理作图法

c.误差曲线取值方法

在数据处理系统直接画出的齿距误差曲线（图9）上，X坐标代表齿序i（此X坐标轴就是图8中的基准线），Y坐标代表齿距误差（以分度圆弧长μm计值），误差曲线在被测齿轮齿数范围内，Y坐标的最大变化量为ΔF_p，相邻两个误差点Y坐标的最大差值为Δf_pt，相隔K个齿距的两个误差点Y坐标的最大差值为ΔF_pk。

图9齿距误差曲线取值法

6.3.1.2跨齿测量

a.计算法

从跨齿测量数据中求取ΔF_p的方法列于表3、4、5、6、7，以Z=60跨齿数N=6，分组数Q=10为例。

表3跨齿齿距累积误差的数据处理

计算结果给出了相对0#齿的跨齿齿距累积误差的最大值ΔF_{pj max}=+10 和最小值ΔF_{pj min}=-11。为了求得ΔF_{pj max}应对i=12～18、i=18～24进行逐齿补点测量。为了求得ΔF_{pj min}应对i=42～48、i=48～54进行逐齿补点测量。补点测量数据的处理方法列于表4、5、6、7。

表4 i= i=12～18逐齿补点数据处理

跨齿序 j	对0齿的跨齿 齿距累积误差 △Fpj	组内测量数据偏差				相对0齿的齿 距累积误差 △Fpi
		齿序 i	相对齿距偏差 (读数值)△Pi′	齿距偏差 △fpti′	相对第12齿的 齿距累积误差△Fpi′
2	+7	12	0 +1 0 +1 -4 -1	+1 +2 +1 +2 -3 0	0	+7
		13			+1	+8
		14			+3	+10
		15			+4	+11
		16			+6	+13
		17			+3	+10
3	+10	18			+3	+10

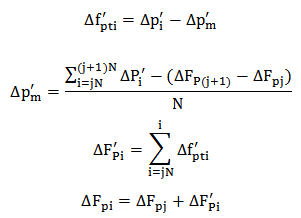
表5 i=18～24逐齿补点数据处理                 μm

跨齿序 j	对0齿的跨齿 齿距累积误差 △Fpj	组内测量数据偏差				相对0齿的齿 距累积误差 △Fpi
		齿序 i	相对齿距偏差 (读数值)△Pi′	齿距偏差 △fpti′	相对第12齿的 齿距累积误差△Fpi′
3	+10	18	0 +1 0 0 0 +1	-1 0 -1 -1 -1 0	0	+10
		19			-1	+9
		20			-1	+9
		21			-2	+8
		22			-3	+7
		23			-4	+6
4	+6	24			-4	+6

表6 i=42～48逐齿补点数据处理                 μm

跨齿序 j	对0齿的跨齿 齿距累积误差 △Fpj	组内测量数据偏差				相对0齿的齿 距累积误差 △Fpi
		齿序 i	相对齿距偏差 (读数值)△Pi′	齿距偏差 △fpti′	相对第12齿的 齿距累积误差△Fpi′
7	-8	42	0 +1 0 +1 +3 +4	-2 -1 -2 -1 +1 +2	0	-7
		43			-2	-10
		44			-3	-11
		45			-5	-13
		46			-6	-14
		47			-5	-13
3	+10	48			-3	-11

表7 i=48～54逐齿补点数据处理                 μm

跨齿序 j	对0齿的跨齿 齿距累积误差 △Fpj	组内测量数据偏差				相对0齿的齿 距累积误差 △Fpi
		齿序 i	相对齿距偏差 (读数值)△Pi′	齿距偏差 △fpti′	相对第12齿的 齿距累积误差△Fpi′
8	-11	48	0 +1 -2 0 0 0	+1 +2 -1 +1 +1 +1	0	-11
		49			+1	-10
		50			+3	-8
		51			+2	-9
		52			+3	-8
		53			+4	-7
9	-6	54			+5	-6

从表4、5求得△F_Pimax=+13μm(i=16)；从表6、7求得△F_Pimin=-14(i=46)。

则：△F_p=△F_pimax-△F_pimin=13-(-14)=27μm。

b.作图法

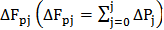
第一步跨齿齿距累积误差图（图10），以直角坐标图上的X坐标代表跨齿序号j，Y坐标代表相对对齿距偏差的累积值（以分度圆弧长μm计值）将测得值（表3中的△P_j）按跨齿序j依次累积标在坐标图上，过原点和最后一个误差点连一直线，该直线即为计算跨齿齿距累积误差的基准线。找出所有误差点中相对基准线的纵坐标最大值为△F_pjmax=+10(i=18)，最小值△F_pjmin=+11(i=48)。

图10跨齿齿距累积误差图

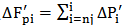
第二步作分组逐齿齿距累积误差图：在直角坐标图上X坐标代表组内齿序号i，Y坐标代表相对齿距偏差的累积值。将测得值（表4中的△P_i′）按齿序i依次累积标在坐标图上，将最后一个误差点的Y坐标减去（△F_p(j+1)-△F_pj）后，与原点连一直线，该直线即为计算组内各齿相对于j齿的齿距累积误差的基准线。作与该基准给Y坐标相距（-△F_pj）的平行线，则此平行线为各齿相对于0#齿的齿距累积误差的基准线。按上述方法分别作i=12～18,i=18～24, i=42～48,i=48～54四组的齿距累称误差图（图11、12、13、14）。并从图中求出△F_pjmax=+13μm，△F_pjmin=-14μm，则△F_p=△F_pjmax-△F_pjmin=13-(-14)=27μm。

图14 i=48～54逐齿齿距累积误差图

6.3.2绝对法测量结果处理

6.3.2.1计算法

从逐齿测量数据中求取Δf_pt、ΔF_p、ΔF_pK的方法见表8。以Z=12，K=2的齿轮为例。

表8绝对法测量数据处理

齿序	公称累积齿距角 φoi	相对0#齿的齿距累积偏差 (读数值)△Fpi	齿距偏差 △fpti=△Fpi-△FP(i-1)	K个齿距累积误差 △F­pki=|△Fpi-△FP(i-k)|
0(12)	0	0	+2 +3 +2 +3 -5 -3 -4 -2 -3 +2 +3 +2	5
1	30°	+2		4
2	60°	+5		5
3	90°	+7		5
4	120°	+10		5
5	150°	+5		2
6	180°	+2		8
7	210°	-2		7
8	240°	-4		6
9	270°	-7		5
10	300°	-5		1
11	330°	-2		5
12	360°	0		5

齿距累积误差△F_p=△F_Pimax-△F_pimin=+10-(-7)=17μm……………………（33）

齿距偏差△f_pt=-5μm……………………（34）

K个齿距累积误差△F_pk=△F_pkimax=8μm………………（35）

6.3.2.2误差曲线取值方法

在由数据处理系统直接画出的齿距误差曲线上取△F_p、△F_pk、△f_pt的方法与6.3.1.1c相同。