摘要：通过对正常齿轮和裂纹齿轮进行动力学仿真研究，发现裂纹齿轮的固有频率要比正常齿轮有明显的降低；进一步研究裂纹深度对齿轮动力学特性的影响，提出了一种诊断齿轮裂纹故障的新方法，并用试验验证了该方法的有效性。

　　关键词：渐开线齿轮；故障建模；裂纹；固有频率；模态分析

　　齿轮传动是机械传动的主要形式之一，被广泛地应用于冶金、石化、矿山、交通运输等工业部门中。但由于齿轮所处的工作环境恶劣等原因，很容易受到损害和出现故障。据统计，传动机械中80%的故障是由齿轮引起的。齿轮的故障将直接影响设备的安全可靠运行，甚至导致整个系统的瘫痪。因此，对齿轮的工作状态的监测及故障诊断技术的研究越来越受到人们的重视。

　　齿轮的失效形式多种多样，其中较常见的裂纹失效是比较严重的一种失效形式，裂纹进一步扩展，就可能导致轮齿疲劳折断，甚至引起整个齿轮的完全失效。因此，对裂纹进行故障机理分析，寻找一种有效的诊断裂纹故障的方法，对齿轮的故障诊断是相当重要的。

　　长期以来，人们在齿根裂纹的诊断方法方面已进行了大量的研究，并取得了很多的成果。常规的诊断方法是振动频谱分析，它以传统的振动理论为依据，利用诊断仪器对其振动的数据和波形进行采集，然后进行分析诊断，找出故障的原因和所在部位。但这样做的前提条件是故障模型的建立要足够准确，才能对故障状态下的振动信号进行正确的识别，这种方式则需要求诊断人员具有较丰富的故障诊断经验。

　　本文从齿轮动力学角度出发，研究了裂纹深度对齿轮固有频率的影响，结果表明，可以将固有频率作为齿轮裂纹故障的一个诊断指标。同时，通过文献可以知道，齿轮的异常振动会激起齿轮本身的固有频率。因此，如果能够精确计算出正常和裂纹齿轮的固有频率值，并且能够在齿轮工作的条件下将其提取出来，对于齿轮的故障诊断工作将有重要的实际意义。

　　1齿轮有限元模态分析

　　模态分析主要用来确定构件或系统的振动特性即固有频率和振型。

　　1.实体模型的建立

　　渐开线齿轮建模的难点是如何比较精确地反映出渐开线廓形和齿根过渡圆角，为了力求较高的计算精度，本文采用在ANSYS中直接建模的方式，其操作流程为。

　　1）编程生成若干齿廓关键点；

　　2）形成一些过渡曲线关键点；

　　3）连点成线，生成较精确的渐开线廓形；

　　4）镜像，生成二维完整齿轮模型；

　　5）拉伸成体；

　　6）对模型进行网格划分。

　　所建立的齿轮模型的几何参数为：齿数Z=20，模数m=4，齿宽b=10mm。材料属性为：杨氏弹性模量E=2.09E11N/m²，泊松比μ= 0.259，材料密度ρ=7.85E3kg/m²。在划分网格时，采用Solid73单元类型和自由网格划分方法，得到如图1所示的有限元模型。

　　文献在ANSYS环境下对齿轮齿根裂纹进行了扩展模拟，模拟结果与实际很吻合。本文在建立裂纹齿轮的模型时，裂纹开口方向和裂纹长度的选取均参照了上述文献所提出的方法，只不过考虑到裂纹加工的方便性，用矩形裂纹代替了圆弧裂纹，裂纹的局部放大图如图2所示。裂纹齿轮单元类型和网格划分方式的选取，均同正常齿轮相同。图中裂纹的深度为5mm，宽度为 0.3mm。

　　1.2约速及加载

　　工作条件下，齿轮和传动轴之间为过盈配合，因此本文的边界条件约束了齿轮内表面各节点X，Y，Z方向的平动自由度和绕X，Y轴的转动自由度。模态是由系统固有特性决定的，与外载荷无关，因此不需要设置载荷边界条件。

　　1.3结果分析

　　本文采用子Block Lanczos法提取了正常齿轮和裂纹齿轮的前10阶自由振动的模态，由于篇幅限制，表1只列出了前6阶固有频率值。

表1   齿轮的固有频率值     Hz

　　从表1可以看出，裂纹齿轮比正常齿轮的固有频率值明显降低。

　　考虑公式

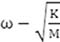
，其中 为固有频率，K为刚度，M为质量。当裂纹出现时，齿轮的质量并没有明显的改变，所以由公式可以推出， 的降低是由于齿轮刚度的下降引起的，这就是为故障齿轮系统的建模提供了一个依据。

　　2裂纹深度变化对固有频率的影响

　　为进一步研究裂纹对构件动力学特性的影响，本文对齿轮齿根裂纹作了更深入的仿真，仿真过程主要针对不同裂纹深度的齿轮展开（深度从小到大，共仿真了14组数据），对各齿轮均提取了其前10阶固有频率值。各阶固有频率随裂纹深度变化的趋势图如图3所示，其中横坐标代表裂纹深度比（裂纹深度和齿根处齿厚之比）；纵坐标为裂纹齿轮和正常齿轮的固有频率比。为便于观察，本文仅画出了前7阶固有频率随裂纹深度变化的趋势图，如图3所示。

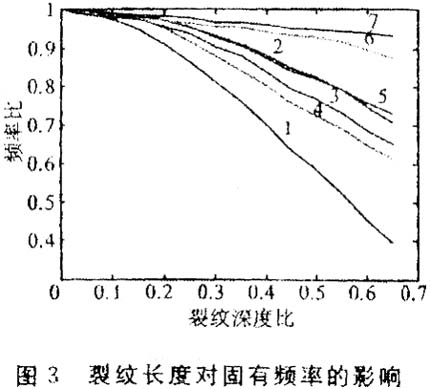
　　从图3可以看出，随着裂纹深度的增加，固有频率呈现明显的下降趋势，尤其是前几阶固有频率受裂纹的影响程度较大。

　　3试验验证

　　3.1实测齿轮箱振动信号

　　为了模仿齿根裂纹，用线切割机在齿根过渡圆角危截面处全齿宽上切割宽0.3mm，深度分别为2mm，3mm，4mm和5mm的裂纹。

　　有限元仿真的正常齿轮的第10阶固有频率为708.17Hz，由采样定理，取采样频率为2048Hz就可以了，采样点数取为2048，输入轴齿轮齿数z₁=20，输出轴齿轮齿数z₂=30，输入轴的回转频率为ƒ_r1=18.55Hz，因此啮合频率ƒ_m=371Hz。图4和图5分别给出了正常齿轮和裂纹齿轮（裂纹深度为4mm）的振动信号时域波形图。

　　3.2模态参数的提取方法

　　通过前面的分析可以知道，齿轮发生裂纹故障时，其模态参数（固有频率）将会发生显著的变化，因此可以考虑将固有频率作为诊断齿轮裂纹故障的一个重要参数。

　　常用的模态分析方法有2种，即有限元理论分析法和试验模态分析法。

　　有限元理论分析法建立的结构动力学模型，不能足够准确的反映实际情况，因此计算的结果会有一定的偏差，但可将有限元计算结果作为试验分析的参考值，进行信号的预处理。

　　传统的试验模态分析法往往是通过测量工程结构在非工作状态下的激振力和响应，进而采用频响函数和脉冲响应函数来识别模态参数。但是对于像齿轮箱这样复杂的机械系统，实现上述测量常常会面临如下困难：激振力的测量难实现；有些情况还不允许停机测试。本文提取模态参数的目的是为了将其用于故障识别，因此，需要寻找一种在线模态识别方法。

　　利用振动信号直接进行模态参数识别的常用方法有Ibrahim时域法、ITD法、最小二乘复指数法、多参考点复指数法、特征系统实现法和ARMA时序分析法。本文采用ARMA时序分析法对齿轮箱振动信号进分析，进而提取系统的模态参数。在以往进行频域谱分时，常由于信号截断而引起泄露，出现旁瓣、分辨率低及信号被淹没等缺陷，而时间序列分析则与频域谱分析不同，由于时序谱是动态谱，观测数据能外延，因此不会由于观测数据的样本长度有限而产生上述缺陷。

　　3.3ARMA时序分析法原理

　　时间序列分析首先由观测数据拟合一个时序模型，然后对该模型进行分析研究，从而得出观测数据的统计特性。由于实测时间序列反映了系统工作的动态过程，因此蕴含着系统的固有特性。建立时序参数模型的目的，就是把系统本身固有的特性很好地表达出来。

　　N个自由度的线性系统激励与响应之间的关系可用高阶微分方程描述，在离散时间域内，该微分方程变成由一系列不同时刻的时间序列表示的差分方程，即ARMA时序模型方程：

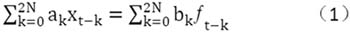
　　式（1）表示响应数据序列X_t与历史值X_t-k，的关系，其中等式左边为自回归（AR）模型，右边为滑动均值（MA）模型，2N为自回归和滑动均值模型的阶次，ak、bk分别表示待识别的自回归系数和滑动均值系数，f_t-k为白噪声激励。

　　运用ARMA时序法识别模态参数首先要估算系数ak和bk的值，本文利用Prony方法对时间序列响应进行拟合获得ARMA模型的参数（可以通过调用MATLAB中的prony函数实现）。当求得自回归系数ak和滑动均值系数bk后，通过ARMA模型传递函数的表达式计算系统的模态参数，ARMA模型的传递函数为：

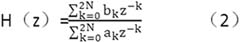
　　用代数方程求解法计算分母多项式方程的根：

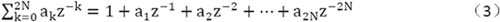
　　求解得到的根为传递函数的极点，他们与系统的模态频率ω_k和阻尼比的关系为：

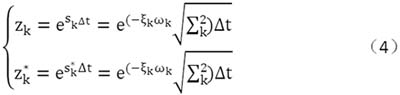
　　由式（4）可求得模态频ω_k和阻尼比，即：

　　3.4模态参数提取结果

　　本文首先用有限元法计算了试验齿轮的前10阶固有频率，并将其作为确定实际信号带通滤波上下限的依据，然后用ARMA时序分析法对滤波后的信号进行处理，提取了不同裂纹深度的齿轮的前5阶固有频率值见表2。

表2     试验提取的固有频率值            Hz

　　从表2的模态参数识别结果来看，随着裂纹深度的增加，提取到的固有频率值也会有所降低，因此将固有频率作为齿轮裂纹故障的诊断参数是可行的。

　　4结语

　　本文提出的方法避免了传统方法诊断所带来的不便之处，并且可以有效地诊断齿轮的齿根裂纹故障诊断中。对于其它类型的故障（如点蚀、磨损等）的诊断，本文也可以为其提供一个很好的参考思路和诊断方法。