简化方法
简化方法是基于一般计算方法经简化得出的,适用于满足下列条件的工业齿轮传动和类似的齿轮传动。
a) 钢制的外啮合和内啮合齿轮;
b) 基本齿廓符合GB 1356;
c) 直齿轮和β≤30°的斜齿轮;
d) 单位齿宽载荷FtH/b≥350N/mm.
应当指出,当FtH/b≥350N/mm时,计算结果偏于安全,当FtH/b<350N/mm时,因为KHa,KFa的实际值较表值大,计算结果偏于不安全。
如果是硬齿面和软齿面相啮合的齿轮副,齿间载荷分配系数取平均值。
如果小齿轮和大齿轮精度等级不同时,则按精度等级较低的取值。
表16的载荷分配系数也可以用于灰铸铁和球墨铸铁齿轮的计算。
表16 齿间载荷分配系数KHa,,KFa的
|
KAFt/b |
≥100N/mm |
<100N/mm |
|
精度等级Ⅱ组 |
5 |
6 |
7 |
8 |
9 |
10 |
11~12 |
5级及更低 |
|
硬齿面
直齿轮 |
KHa, |
1.0 |
1.1 |
1.2 |
1/Z2ε≥1.2 |
|
KFa |
1/Yε≥1.2 |
|
硬齿面
斜齿轮 |
KHa, |
1.0 |
1.1 |
1.2 |
1.4 |
εa/cos2βb≥1.4 |
|
KFa |
|
非硬齿面
直齿轮 |
KHa, |
1.0 |
1.1 |
1.2 |
1/Z2ε≥1.2 |
|
KFa |
1/Yε≥1.2 |
|
非硬齿面
斜齿轮 |
KHa, |
1.0 |
1.1 |
1.2 |
1.4 |
εa/cos2βb≥1.4 |
|
KFa |
|
注
1 经修形的6级精度硬齿面斜齿轮,取KHa,= KFa =1。
2 表右部第5,8行若计算K Fa> 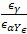 ,则取K Fa= 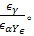 。 3 Zε,Yε分别见7.1.3和7.2.3。 |
|
|
|
|
|
|
|
|
|
|
6.4.3 齿廓跑合量ya.
齿廓跑合量是在齿轮运转初期,由于跑合使初始基节极限偏差减小的量;其值沿齿廓法线方向计量。
ya可按表17中的公式近似计算。
表17 齿廓跑合量ya
|
齿轮材料 |
齿廓跑合量ya/μm |
限制条件 |
|
结构钢、调质钢、珠
光体和贝氏体球墨铸铁 |
y a=  (145) |
υ>10m/s 时,
y a≤ 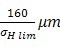 ,f pb≤40μm 5<υ≤10m/s 时,
y a≤ 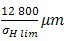 ,f pb≤80μm υ≤5m/s 时, ya无限 |
|
铁、素体球墨铸铁 |
ya=0.275fpb (146) |
υ>10m/s 时, υ≤11μm, fpb≤40μm;
5<υ≤10m/s 时,ya≤22μm, fpb≤80μm
υ≤10m/s 时,ya无限制 |
|
渗碳淬火钢或氮化钢、氮碳共渗钢 |
ya=0.075fpb (147) |
ya≤3μm |
|
注
1 fpb——齿轮基节极限偏差,μm;σHlim——齿轮接触疲劳极限,N/mm2,见图8.1.2。
2 当大、小齿轮的材料和热处理不同时,其齿廓跑合量可取为相应两种材料齿轮副跑合量的算术平均值。 |
6.5 轮齿刚度c’,cy
6.5.1 定义及影响因素
轮齿刚度定义为使一对或几对同时啮合的精确轮齿在1mm齿宽上产生1μm挠度所需的啮合线上的载荷。
直齿轮的“单对齿刚度”c’是指一对轮齿的最大刚度,大致等于单齿啮合状态下一对轮齿的刚度。斜齿轮的c’是指一对轮齿在法截面内的最大刚度。Cy是端面内轮齿总刚度的平均值,简称“啮合刚度”。
影响轮齿刚度的主要因素有:
a) 轮齿参数,如齿数、基本齿廓、齿高修正,螺旋角、端面重合度;
b) 轮体结构,如轮缘厚度和辐板厚度;
c) 法截面内单位齿宽载荷;
d) 轴毂联接结构和形式;
e) 齿面粗糙度和齿面波度;
f) 齿向误差;
g) 齿轮材料的弹性模量。
轮齿刚度的精确值应考虑所有影响因素经全面分析而确定。可以由实验结果直接得到,也可以由基于弹性理论的有限元法计算确定。在上述方法由于理论和技术上的困难而难以实现时,可按下述方法之一确定轮齿刚度。
6.5.2 一般方法
对于基本齿廓符合GB1356、单位齿宽载荷FAFy/b≥100N/mm、轴-毂处圆周方向传力均匀(小齿轮为轴齿轮形式、大轮过盈联接或花键联接)、钢质的直齿轮和螺旋角β≤45°的外啮合齿轮,c’和cy可按给出的计算公式和线图确定。对于不满足上述条件的齿轮,如内啮合,非钢质材料的组合,其他形式的轴-毂联接,单位齿宽载荷FAFy/b<100N/mm的齿轮,c’和cy也可近似地应用。
6.5.2.1 单对齿刚度c’
单对齿刚度c’由式(148)确定:
c’= c’thCMCRCBcosβ…………………………………………………………………………….(148)
式中:c’th——单对齿刚度的理论值,N/(mm·μm),见6.5.2.1a;
CM——理论修正系数,见6.5.2.1b;
CR——轮坯结构系数,见6.5.2.1c;
CB——基本齿廓系数,见6.5.2.1d;
a) 单对齿刚度的理论值 c’th,
c’th值可由式(149)3)(3)该式中的c th′值是在单对齿宽载荷Ft/b=300N/mm条件下的钢钢齿传输线经分析得到的。对于斜齿轮按当量齿轮计算)计算。
c’
th=
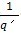
…………………………………………………………………………(149)
式中:q’为轮齿柔度的最小值,mm·μm/N。
93X2±0.241 88 +0.005 29X21+0.001 82 X22……………………………50)6](6]式(150)已将ISO6336-1:1996式(9.03)中某些排版差错(如zn1与zn2颠倒,CB=0.000529等)订正。)
式中:zn1,zn2——小、大(斜)齿轮当量齿数。对于内啮合齿轮,式中(150)中的,zn2应取为无限大。
3)该式中的c’th值是在单对齿宽载荷Ft/b<300N/mm条件下的钢制齿轮经分析得到的。对于斜齿轮按当量齿轮计算。
采用说明:
6]式(150)已将ISO6336-1:1996式(9 .03)中某些排版差错(如zn1与zn2颠倒,C8=0.000 529等)订正。
b)理论修正系数CM
CM考虑实验值对理论值的修正。一般取CM=0.8。
C)轮坯结构系数CR
CR考虑齿轮的轮缘和辐板结构的影响。对于实心齿轮,可取CR=1。
非实心齿轮可按轮缘厚度SR和辐板厚度bs由式(151)计算。
C
R=1+
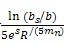
………………………………………………….(151)
若bs/b<0.2,取bs/b=0.2;若bs/b>1.2,取bs/b=1.2;若SR/mn<1,取SR/mn=1。
d)基本齿廓系数CB
CB考虑实际基本齿廓与标准基本齿廓的差别对单对齿刚度的影响。CB由式(152)计算。
CB =〔1+0.5(1.2-htp/mn)〕·〔1-0.02(20°-an)〕………(152)
对基本齿廓符合a=20°,hap=mn,hfp=1.2mn,ρfp=0.2的齿轮(hap,hfp和ρfp见表1及图14),CB=1。
若小轮和大轮的齿根高不一致,GB如下计算:
CB=0.5(CB1+CB2)…………………………………………(153)
式中:CB1——小轮的基本齿廓系数,按式(152)确定;
CB2——大轮的基本齿廓系数,按式(152)确定。
e)附加说明
1)式(148)只适用于钢对钢齿轮,对于其他材料配对的情况,单对齿刚度C′可按下式计算:
C′= C′stζ…………………………………(154)
式中:ζ=
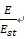
E=
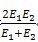
C′st 为钢C′,Est为钢的E;
对钢与铸铁配对:ζ=0.74
对铸铁与铸铁配对:ζ=0.59
2)式(148)适用于单位齿宽载荷FAFt/b≥100N/mm的情况,对于FAFt/b<100N/mm的情况,C′应作修正:
C′= C′stC
MC
RC
Bcosβ
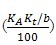 0.25
0.25…………………………………………………(155)
3)一对齿轮副中,若一个齿轮为平键联接,配对齿轮为过盈或花键联接,由式(148)计算的C′增大5%;若两个齿轮都为平键联接,由式(148)计算的C′增大10%。
6.5.2.2啮合刚度cy
Cy=(0.75εa+0.25) C′………………………………………………(156)
式中:C′——单对齿刚度,见6.5.2.1;
εa——端面重合度。
上式适用于齿轮和螺旋角β≤30°的斜齿轮。对εa<1.2的直齿轮的cy,需将式(156)计算值减小10%。
6.5.3 简化方法
基本齿廓符合GB 1356的钢制刚性盘状齿轮,当β≤30°,1.2<εa<1.9时且FtFA/b≥100N/mm,可取:
单对齿刚度C′=14N/(mm·μm)
啮合刚度 cy=20N/(mm·μm)
非实心齿轮的C′,cy可用轮坯结构系数CR(见6.5.2.1)折算。
其他的基本齿廓的齿轮C′,cy可用基本齿廓系数CB(见6.5.2.1)折算。
非钢对钢配对的齿轮的C′,cy可用式(156)折算(见6.5.2.1)。
7 修正计算应力的系数
7.1计算接触应力的系数
7.1.1 节点区域系数ZH
节点区域系数ZH是考虑节点处齿廓曲率对接触应力的影响,并将分度圆上切向力折算为节圆上法向力的系数。
ZH数值可由式(157)计算得出。对于具有法面齿形角an为20°,22.5°25°的内、外啮合齿轮,ZH也可由图7、图8和图9根据比值(X2+X1)/(Z2+Z1)及螺旋角β查得。
图7 an=20°时的节点区域系数ZH
图8 an=22.5°时的节点区域系数ZH
Z
H=
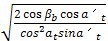
………………………………………………………(157)
式中:at——端面分度圆压力角;
a
t =arctan

…………………………………………………………(158)
βb——基圆螺旋角;
βb =arctan(tanβcos at)…………………………………………(159)
aˊt——端面啮合角;
inv a
ˊt=inv a
t+
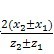
tan a
n……………………………………(160)
上式中“+”用于外啮合,“-”用于内啮合。
图9 an=25°时的节点区域系数ZH
7.1.2 弹性系数ZE
弹性系数ZE是用以考虑材料弹性模量E和泊桑比对赫兹应力的影响。其数值可按实际材料弹性模量E和泊桑比ν由式(161)计算得出。对于某些常用材料组合的ZE可参考表18查取。
Z
E=
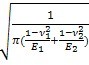
………………………………………………………………(161)
当两齿轮材料均匀钢时,E1=E2=E,V2=V2=V,则
Z
E=
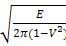
…………………………………………………………………(162)
当两齿轮材料的弹性模量不同时,其当量弹性模量为;
E=
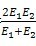
…………………………………………………………(163)
表18 弹性系数ZE
|
齿轮 1 |
齿轮 2 |
ZE |
|
材料 |
弹性模量
E1(N/mm2) |
泊桑比
V1 |
材料 |
弹性模量
E2(N/mm2) |
泊桑比
V2 |
|
|
钢 |
206 000 |
0.3 |
钢 |
206 000 |
0.3 |
189.8 |
|
铸钢 |
202 000 |
188.9 |
|
球墨铸铁 |
173 000 |
181.4 |
|
灰铸铁 |
118 000~126 000 |
162.0~165.4 |
|
铸钢 |
202 000 |
0.3 |
铸钢 |
202 000 |
0.3 |
188.0 |
|
球墨铸铁 |
173 000 |
180.5 |
|
灰铸铁 |
118 000 |
161.4 |
|
球墨铸铁 |
173 000 |
0.3 |
球墨铸铁 |
173 000 |
0.3 |
173.9 |
|
灰铸铁 |
118 000 |
156.6 |
|
灰铸铁 |
118 000~126 000 |
0.3 |
灰铸铁 |
118 000 |
0.3 |
143.7~146.70 |
7.1.3 重合度系数Zε
重合度系数Zε是用以考虑重合度对单位齿宽载荷的影响。Zε可由式(164)、(165)、(166)计算得出,也可根据端面重合度εa和纵向重合度εβ由图10查得。
图10 重合度系数Zε
直齿轮:
Z
ε=
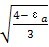
…………………………………………(164)
斜齿轮:
当εβ<1时,
Z
ε=
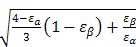
……………………………………(165)
当εβ≥1时
Z
ε=
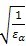
……………………………………………………(166)
以上式中;εβ——端面重合度,
ε
β=
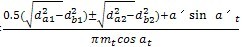
…………………………(167)
εβ——纵向重合度,
ε
β=
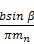
……………………………(168)
εβ计算式中,符号“±”和“ ”,上面的用于外啮合传动,下面的用于内啮合传动;
εβ计算式中,当大小齿轮的齿宽b不一样时,采用其中较小值。对人字齿,b=2bB,bB为单个斜齿宽度。
7.1.4 螺旋角系数Zβ
螺旋角系数Zβ是考虑螺旋角造成的接触线倾斜对接触应力影响的系数。Zβ数值可由式(169)计算,也可根据分度圆螺旋角β由图11查得。
Z
β=

………………………………………………(169)
图11 螺旋角系数Zβ
7.1.5 单对齿啮合系数ZB,ZD
ZB是把节点C处的接触应力折算到小轮单对齿啮合区内界点B处的接触应力的系数;ZD则是把节点C处的接触应力折算到大轮单对齿啮合区内界点D处的接触应力的系数(参见图12)。
ZB和ZD可由下述的计算来得到。
端面重合度εa2的外啮合齿轮4)(4)对于端面重合度,2<εα<3的外啮合齿轮,ZB和ZD按两对齿啮合的外界点计算):
先计算参数M1和M2:
M
1=
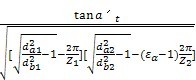
……………………(170)
M
2=
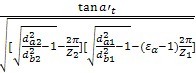
……………………(171)
式中da1(da2),db1(db2),Z1(Z2)分别为小轮(大轮)的齿根圆、基圆直径和齿数;a′t为端面分度圆啮合角,见式(160);εa为端面重度,见式(167)。
直齿轮:
当M1>1时,ZB=M1;当M1≤1时,ZB=1。
当M2>1时,ZD=M2;当M2≤1时,ZD=1。
斜齿轮:
当纵向重合度εβ≥1.0时,ZB=1,ZD=1。
当纵向重合度εβ<1.0,ZB、ZD由式(172),式(173)确定。
ZB= M1-εβ(M1-1)……………………………(172)
当ZB<1时,取ZB=1。
ZD= M2-εβ(M2-1)……………………………(173)
当ZD<1时,取ZD=1。
对内啮合齿轮,取ZB=1,ZD=1。
图12 节点C及单对齿啮合区B、D处的曲率半径
4)对于端面重合度,2<εa<3的外啮合齿轮,ZB和ZD按两对齿啮合的外界点计算。
7.2 计算弯曲应力的系数
7.2.1 齿形系数YF,YFa
齿形系数是用以考虑齿形对名义弯曲应力的影响,以过齿廓根部左右两过渡曲线与30°切线相切点的截面作为危险截面进行计算。
7.2.1.1 齿形系数YF
齿形系数YF是考虑载荷作用于单对齿啮合区外界点时齿形对名义弯曲应力的影响(参见图13)。
a) 外齿轮的齿形系数YF
按图13所示定义,外齿轮的齿形系数可YF由下式确定:
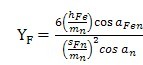
…………………………………(174)
式中:mn——齿轮法向模数,mm;
an——法向分度圆压力角;
aFen,hFe,sFn的定义见图13。
式(174)适用于标准或变位的直齿轮和斜齿轮。对于斜齿轮,齿形系数按法截面确定,即按当量齿数zn进行计算。大、小轮的齿形系数应分别确定。Zn应按式(178)计算。
用齿条刀具加工的外齿轮的YF可用表19中的公式计算。
本计算方法需满足下列条件:
1)30°切线的切点应位于由刀具齿顶圆角所展成的齿根过渡曲线上;
2)刀具齿顶必须有一定大小的圆角,即ρfp≠0。刀具的基本齿廓尺寸见图14。
图13 影响外齿轮齿形系数YF的各参数
图14刀具基本齿廓尺寸
表19 外齿轮齿形系数YF的有关公式
|
序号 |
名称 |
代号 |
计算公式 |
公式号 |
备注 |
|
1 |
刀尖圆心至刀齿
对称线的距离 |
E |
|
(175) |
hfp——基本齿廓齿根高
Spr=Pr-q见图14 |
|
2 |
辅助值 |
G |
|
(176) |
x——法向变位系数 |
|
3 |
基圆螺旋角 |
Βb |
arcos[ 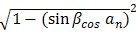 ] |
(177) |
|
|
4 |
当量齿数 |
Zn |
|
(178) |
|
|
5 |
辅助值 |
H |
|
(179) |
用牛顿法解时可取初始值
θ=-H/(1-2G/ zn) |
|
6 |
辅助值 |
θ |
(2G/zn)tanθ-H |
(180) |
|
|
7 |
危险截面齿厚与
模数之比 |
|
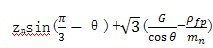 |
(181) |
|
|
8 |
切点处曲率半径
与模数之比 |
|
|
(182) |
|
|
9 |
当量直齿轮端面
重合度 |
εan |
|
(183) |
εa见式(167) |
|
10 |
当量直齿轮分度
圆直径 |
dn |
|
(184) |
|
|
11 |
当量直齿轮基
圆直径 |
dbn |
dncos an |
(185) |
|
|
12 |
当量直齿轮顶
圆直径 |
dan |
dn+dn-d |
(186) |
dn –齿顶圆直径
d-分度圆直径 |
|
13 |
当量直齿轮单对齿
啮合区外界点直径 |
den |
注:式中“ ”处对外啮取“一”,对内啮合取“+” (187)7](7]式(187
相应的ISO6336-3:1996式(4.16)有误,已订正) |
|
14 |
当量齿轮单齿啮合
外界点压力角 |
aen |
arcos 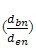 |
(188) |
|
|
15 |
外界点处的齿厚半角 |
ye |
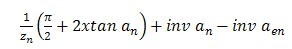 (189) |
|
16 |
当量齿轮单齿啮合
外界点载荷作用角 |
aFen |
aen-ye |
(190) |
|
|
17 |
弯曲力臂与
模数比 |
|
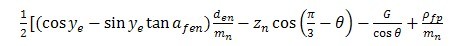 (191) |
|
18 |
齿形系数 |
YF |
|
(174) |
|
|
注:在表中19至表22中,长度单位为mm;角度单位为rad. |
b) 内齿轮的齿形系数YF
内齿轮的齿形系数YF不仅与齿数和变位系数有关,且与插齿刀的参数有关。为了简化计算,可近似地按替代齿条计算(见图15)。替代齿条的法向齿廓与基本齿条相似,齿高与内齿轮相同,法向载荷作用角aFen等于an,并以脚标2表示内齿轮,有关计算公式见表20(适用于z2>70)。
图15 影响内齿轮齿形系数YF的各参数
采用说明:
7]式(187)相应的ISO6336-3:1996式(4.16)有误,已订正。
由于内齿轮通常用齿轮形刀具切制而成,其齿根过渡圆弧半径ρF2常常是较小的。当ρF2未知时,可近似取ρF2=0.15ma.
表20 内齿轮齿形系数YF的有关公式
|
序号 |
名称 |
代号 |
计算公式 |
公式号 |
备注 |
|
1 |
当量内齿轮分度圆直径 |
dn2 |
|
(192) |
d2——内齿轮分度圆直径 |
|
2 |
当量内齿轮根圆直径 |
dfn2 |
dn2+df2-d2 |
(193) |
df2——内齿轮根圆直径 |
|
3 |
当量齿轮单齿啮合区外界点直径 |
den2 |
同表19式(187) |
(187) |
式中“ ”、
“ ”符号应
采用内啮合的 |
|
4 |
当量内齿轮齿根高 |
hfp2 |
|
(194)8] |
|
|
5 |
内齿轮齿根过渡圆半径 |
ρF2 |
当ρF2已知时取已知道;
当ρF2未知时取为0.15m. |
(195) |
|
|
6 |
刀具圆角半径 |
ρFp2 |
当齿轮型插齿刀顶端ρfp2已知时取
已知值;当ρfp2未知时,取
ρfp2≈ρF2 |
(196) |
|
|
7 |
危险截面齿厚与模数之比 |
|
|
(197)9] |
Spr=Pr-q,
见图14 |
|
8 |
弯曲力臂与模数之比 |
|
|
(198)10] |
|
|
9 |
齿形系数 |
YF |
|
(174a) |
|
采用说明:
8]式(194)相应的ISO6336-3:1996式(4.3)定义不合我国惯用定义,已订正。
9]ISO6336-3:1996式(4.21)首项误为1/2,已订正为2。
10]已按8]订正将式(1980中有关符号变号。
7.2.1.2齿形系数YFa
齿形系数YFa是考虑当载荷作用于齿顶时齿形对名义弯曲应力的影响,用于近似计算。YFa只能与Yt一起作用。
a) 外齿轮的齿形系数YFa按图16定义,并可由下式确定:
Y
Fa=
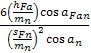
采用说明:
8]式(194)相应的ISO6336-3:1996式(4.23)定义不合我国惯用定义,已订正。
9]ISO6336-3:1996式(4.21)首项误为1/2,已订正为2。
10]已按8]订正将式(198)中有关符号变号。
式(199)适用于εan<2的标准或变位的直齿轮和斜齿轮。大、小轮的YFa应分别确定。
对于斜齿轮,齿形系数按法截面确定,即按当量齿数Zn确定,当量齿数Zn可用式(178)计算。
用齿条刀具加工的外齿轮的YFa可按表21中的公式计算,或按图18a~18d相应查取。不同参数的齿形所适用的图号见表23。
图18a~18d的图线适用于齿顶不缩短的齿轮。对于齿顶缩短的齿轮,实际弯曲力臂比不缩短时稍小一些,因此用以上图线查取的值偏于安全。
图16 影响外齿轮齿形系数YFa的各参数
表21 外齿轮齿形系数YFa的有关公式
|
序号 |
名称 |
代号 |
计算公式 |
公式号 |
备注 |
|
1 |
刀尖圆心至刀齿对称线的距离 |
E |
|
(175) |
hfp——基本齿廓齿根高
spr——pr-q,见图13 |
|
2 |
辅助值 |
H |
|
(176) |
x——法向变位系数 |
|
3 |
基圆螺旋角 |
βb |
arccos[ 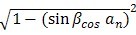 ] |
(177) |
|
|
4 |
当量齿数 |
zn |
|
(178) |
|
|
5 |
辅助值 |
H |
|
(179) |
|
|
6 |
辅助角 |
θ |
(2G/zn)tanθ-H |
(180) |
用牛顿法解时可取初始值
θ=-H/(1-2G/zn) |
|
7 |
危险截面齿厚与模数之比 |
|
|
(200) |
/mn按式(182)计算 |
|
8 |
当量齿轮齿顶压力角 |
aan |
arcos[  ] |
(201) |
da——齿顶圆直径
d——齿分圆直径 |
|
9 |
齿顶厚半角 |
ya |
|
(202) |
|
|
10 |
当量齿轮齿顶载荷作用角 |
aFan |
a an-y a=tan a an-inv a n- 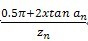 |
(203) |
|
|
11 |
弯曲力臂与模数之比 |
|
|
(204) |
|
|
12 |
齿形系数 |
YFa |
|
(199) |
|
b) 内齿轮的齿形系数YFa
内齿轮的齿形系数YFa可近似地按替代齿条计算。此替代齿条的法向齿廓与基本齿条相似,齿高与内齿轮相同,并取法向载荷作用角aFan等于an(参见图17)。以脚标2表示内齿轮。有关计算公式见表22(适用于z2>70)。
与图18a18e各齿形参数相对应的内齿轮齿形系数YFa也可由表23查取。
表22 内齿轮齿形系数YFa的有关公式
|
序号 |
名称 |
代号 |
计算公式 |
公式号 |
备注 |
|
1 |
当量内齿轮分圆直径 |
dn2 |
|
(192) |
d2——内齿轮分圆直径 |
|
2 |
当量内齿轮根圆直径 |
dfn2 |
dn2+ df2- d2 |
(193) |
df2——内齿轮根圆直径 |
|
3 |
当量内齿轮顶圆直径 |
dan2 |
dn2+ da2- d2 |
(205) |
da2——内齿轮顶圆直径 |
|
4 |
当量内齿轮齿根高 |
hfp2 |
|
(194) |
|
|
5 |
内齿轮齿根过渡圆半径 |
ρF2 |
当ρF2已知时取已知值;当ρF2未知时取为0.15mn |
(195) |
|
|
6 |
刀具圆角半径 |
ρfp2 |
当齿轮型插齿刀顶端ρfp2已知时取已知值;当ρfp2未知时取ρfp2≈ρF2 |
(196) |
|
|
7 |
危险截面齿厚与模数之比 |
|
|
(197) |
spr=pr-q见图14 |
|
8 |
弯曲力臂与模数之比 |
|
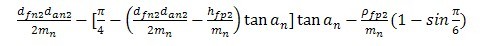 (206) 11] |
|
9 |
齿形系数 |
YFa |
(6hFa2/mn)/( shFn2/mn)2 (199a) |
|
注:对变位齿轮,仍取标准齿高。 |
采用说明:
11]已按8]订正将式(206)中有关符号变号。
图17影响内齿轮齿形系数YFa的各参数
表23 几种基本齿廓齿轮的YFa
|
基本齿廓 |
外齿轮 |
内齿轮 |
|
an |
|
|
|
YFa |
YFa
ρF=0.15mn,h=hap+hfp |
|
20° |
1 |
1.25 |
0.38 | ,
图18a |
2.053 |
|
20° |
1 |
1.25 |
0.3 |
图18b |
2.053 |
|
22.5° |
1 |
1.25 |
0.4 |
图18c |
1.87 |
|
20° |
1 |
1.4 |
0.4 |
图18d |
(已挖根) |
|
25° |
1 |
1.25 |
0.318 |
图18e |
1.71 |
注:an=20°;hap/ mn =1.0,hfp/mn=1.25;ρfp/mn=0.38
对内齿轮:当ρF=0.15 mn,hfp=1.25 mn,hap= mn时,YFa=2.053
图18a 外齿轮齿形系数YFa
注:an=20°;hap/mn=1.0,hfp/mn=1.25;ρfp/mn=0.3
对内齿轮:当ρF=0.15 mn,hfp=1.25 mn,hap=mn时,YFa=2.053
图18b外齿轮齿形系数YFa
注:an=22.5°;hap/mn=1.0,hfp/mn=1.25;ρfp/mn=0.4
对内齿轮:当ρF=0.15 mn,hfp=1.25 mn,hap=mn时,YFa=1.87
图18c 外齿轮齿形系数YFa
注:an=20°;hap/mn=1.0,hfp/mn=1.4;ρfp/mn=0.4;spr=0.02mn
图18d 外齿轮齿形系数YFa
注:an=25°;hap/mn=1.0,hfp/mn=1.25;ρfp/mn=0.318
图18e 外齿轮齿形系数YFa
7.2.2 应力修正系数Ys,Ysa
应力修正系数Ys和Ysa是将名义弯曲应力换算成齿根局部应力的系数。它考虑了齿根过渡曲线处的应力集中效应,以及弯曲应力以外的其他应力对齿根应力的影响。
应力修正系数不仅取决于齿根过渡曲线的曲率,还和载荷作用点的位置有关。Ys用于载荷作用于单对齿啮合区外界点的计算方法(方法一),Ysa则用于载荷作用于齿顶的计算方法(方法二)。
7.2.2.1 应力修正系数Ys
应力修正系数Ys仅能与齿形系数YF联用。对于an齿形角为20°的齿轮,Ys可按式(207)计算。对于其他齿形角的齿轮,可按此式近似计算Ys.
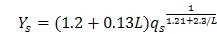
……………………………(207)
上式适用范围为:1≤qs<8
式中:L——齿根危险截面处齿厚与弯曲力臂的比值:
L=
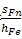
…………………………(208)
sFn——齿根危险截面齿厚。外齿轮由式(181)计算,内齿轮按式(197)计算。
hFe——弯曲力臂。外齿轮由式(191)计算,内齿轮由式(198)计算。
qs——齿根圆角参数,其值为:
q
s=
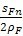
………………………………(209)
ρF——30°切线切点处曲率半径。外齿轮由式(182)计算,内齿轮由式(195)计算。
Ys不宜用图解法确定。
7.2.2.2应力修正系数Ysa
应力修正系数Ysa仅能与齿形系数YFa联用,并且只能用于εan<2的齿轮传动。
对于齿形角an为20°的齿轮,Ysa可按式(210)计算。对于其他齿形角的齿轮,可按此式近似计算Ysa。
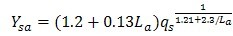
………………………(210)
上式适用范围为1≤qs<8,
式中:La=sFn/hFa;
sFn——外齿轮由式(181)计算,内齿轮由式(197)计算;
hFn——外齿轮由式(204)计算,内齿轮由式(206)计算;
qs——按式(209)计算。
用齿条刀具加工的外齿轮,其应力修正系数Ysa也可按当量齿数和法向变位系数从图19a~19e查取。对于短齿和有齿顶倒角的齿轮来说,使用这些图中的Ysa值,其承载能力是偏向安全的。不同参数的齿形所适用的图号见表24。
表24 几种基本齿廓齿轮的Ysa
|
基本齿廓 |
外齿轮 |
内齿轮 |
|
an |
|
|
|
Ysa |
Ysa
ρF=0.15mn,h=hap+hfp |
|
20° |
1 |
1.25 |
0.38 |
图19a |
2.65 |
|
20° |
1 |
1.25 |
0.3 |
图19b |
2.65 |
|
22.5° |
1 |
1.25 |
0.4 |
图19c |
2.76 |
|
20° |
1 |
1.4 |
0.4 |
图19d |
(已挖根) |
|
25° |
1 |
1.25 |
0.318 |
图19e |
2.87 |
注:an=20°;hap/mn=1.0,hfp/mn=1.25;ρfp/mn=0.38
对内齿轮:当ρF=0.15mn,hfp=1.25mn,hap=mn时,YSa=2.65
图19a 外齿轮应力修正系数Ysa
注:an=20°;hap/mn=1.0,hfp/mn=1.25;ρfp/mn=0.3
对内齿轮:当ρF=0.15mn,hfp=1.25mn,hap=mn时,YSa=2.65
图19b 外齿轮应力修正系数Ysa
注:an=22.5°;hap/mn=1.0,hfp/mn=1.25;ρfp/mn=0.4
对内齿轮:当ρF=0.15mn,hfp=1.25mn,hap=mn时,YSa=2.76
图19c 外齿轮应力修正系数Ysa
注:an=20°;hap/mn=1.0,hfp/mn=1.4;ρfp/mn=0.4;spr=0.02mn
图19d 外齿轮应力修正系数Ysa
注:an=25°;hap/mn=1.0,hfp/mn=1.25;ρfp/mn=0.318
图19e 外齿轮应力修正系数Ysa
7.2.2.3 齿根有磨削台阶齿轮的应力修正系数
靠近齿根危险截面的磨削台阶(参见图20),将使齿根的应力集中增加很多,因此其应力集中系数相应地要增加。计算时应当用式(211)的Ysg代替式(207)Ys,用公式(212)的Ysag代替式(210)Ysa.
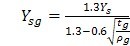
……………………………………(211)
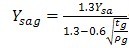
……………………………………(212)
上述二式仅适用于
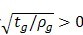
的情况。
当磨削台阶高于齿根30°切线切点时,其磨削台阶的影响将比式(211)和式(212)计算所得的小。
Ysg和Ysag也考虑了齿根厚度的减薄。
图20齿根磨削台阶
7.2.3弯曲强度计算的重合度系数Yε
重合度系数Yε是将载荷由齿顶转换到单对齿啮合区外界点的系数。
Yε可用式(213)计算。
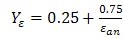
………………………………(213)
式中:
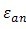
——当量齿轮的端面重合度。
7.2.4 弯曲强度计算的螺旋角系数Yβ
螺旋角系数Yβ是考虑螺旋角造成的接触线倾斜对齿根应力产生影响的系数。其数值可由式(214)和(215)计算。
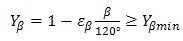
…………………………………(214)
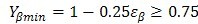
………………………………(215)
上面式中:当εβ>1时,按εβ=1计算,当Yβ<0.75时,取Yβ=0.75;当β>30°时,按β=30°计值。
螺旋角系数Yβ也可根据β角和纵向重合度εβ由图21查取。
图21 螺旋角系数Yβ