3.1弹性联轴器的刚度和阻尼
弹性联轴器由于具有能产生较大弹性变形和阻尼作用的弹性元件，因此除能补偿两轴相对位移外，还能起缓冲和吸振的作用。弹性联轴器能适应载荷的波动，所以其应用较广，类型也较多。这种联轴器的缓冲和吸振性能主要与其刚度和阻尼有关。

联轴器的刚度可分为径向刚度、周向刚度和扭转刚度。由于载荷变化多数以扭矩波动形式出现，由此引起的振动也是以扭转振动为主，所以联轴器最主要的刚度是扭转刚度。扭转刚度易产生单位扭转变形所需的扭矩表示。通常，由于传动轴系中其它零件的刚度都比弹性联轴器的刚度大得多。所以为了简化起见，其它零件的弹性可以略去不计。仅考虑联轴器弹性，并根据这一情况以联轴器的刚度作为传动轴系的刚度。刚度可用下式表示：
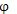
C=T/                                  （3-1）

式中T——联轴器传递的扭矩；

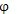
——在扭矩作用下两半联轴器的相对扭转角。
当轴系接近发生共振时，刚度随扭矩增大而增大，改变传动轴系的固有频率与振动频率之间的关系，就能避开共振。
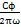
弹性联轴器在传递不稳定扭矩的过程中，弹性元件的弹性变形随扭矩的改变而增减。由于变形的不稳定，在弹性元件相对运动的接触表面上产生外摩擦，同时在弹性元件内部还存在内摩擦。这些摩擦将吸收一部分动能转化为热能，使温度升高。这就是联轴器的阻尼作用。阻尼作用能实现缓冲和衰减振动。联轴器的阻尼性能可以用阻尼系数表示。它是每一次载荷循环中产生的阻尼能和储存在扭转弹性元件中的变形能之比，即ф=W_d/W_e。在振动运动微分方程中，粘滞阻力系数用y来表示，它与阻尼系数之间的关系为Y= ，ω为振动频率或绕动力矩变化频率。阻尼系数大，由于摩擦而消耗的能量就多，反之，阻尼系数小，由于摩擦而消耗的能量就少。
弹性联轴器一般都有缓冲和吸振功能，但是具有某一定值弹性的联轴器，并不是在任意的变扭矩作用下都能产生减振的效果，有时反而会引起更强烈的振动。其原因不在于此联轴器的刚度大小。可见，只有刚度和整个传动轴系的其他参数和载荷协调时，才能产生减振效果。因此，必须根据课题条件，通过计算来定出联轴器的刚度。

3.2周期性载荷作用下的动力特性计算

对于某一已定的传动轴系，转动惯量和固有频率可由计算求得，如果已知所传扭矩的变化规律，如振幅和频率等，就能建立起轴系在扭转振动式的运动微分方程，对该方程求解，即可得到所需的联轴器的刚度。
为了便于求解运动微分方程，需要对传动轴系中联轴器的主动和从动两侧的转动惯量和刚度作力学模型的简化。根据具体结构情况，可以将轴系简化为若干个等效转动惯量圆盘，以具有某一刚度的周联系起来。通常比较典型的是简化为两个等效的圆盘，配置在联轴器的两侧。并设定所联两轴的刚性很大，只有联轴器具有弹性和阻尼。如图3.1所示

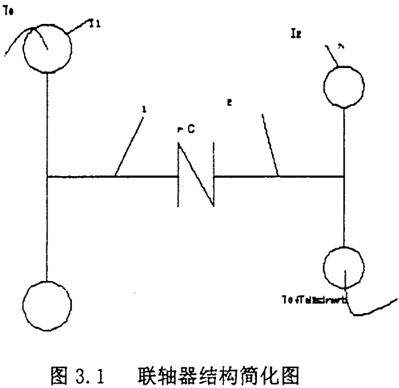
设定主动轴与圆盘1以恒扭矩经联轴器带动从动轴上的圆盘2，而在从动圆盘上有按简谐规律变化的扰动扭矩分量。此时，根据动量矩定理，按联轴器两侧力矩平衡条件，可以分别列出两圆盘的转动运动方程式，即系统扭振的微分方程为：
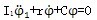
                                               （3-2）

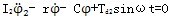
                                   （3-3）

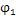
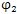
式中 ， ——主从动圆盘的转角

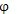
--两圆盘的相对扭转角

I₁,I₂——主、从动轴上圆盘的等效转动惯量

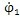
， ——主、从动轴的角速度

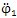
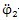
， ——主、从动轴的角加速度

C——联轴器的刚度
r——联轴器粘滞阻力系数
T_d2sinωt——从动轴圆盘上的扰动扭矩
以上两式合并得到二阶常系数线性非其次微分方程

上式的解由两部分组成，即对应的其次方程的通解和本方程的特解。经运算后可得到联轴器所受的谐振扭矩为：

当sin（ωt+a）=l时，表示谐振扭矩达到最大值：

由上式可知，在有阻尼的受迫振动中，经连轴器传递振动扭矩的振幅，主要与动力放大系数和转动惯量有关。当扰动扭矩作用一侧的转动惯量大于另一侧的转动惯量时，可以减小振动扭矩的振幅。反之，对减小振动扭矩振幅的作用不大。动力放大系数对振动扭矩振幅的影响与阻尼系数、扰动扭矩的变化频率及轴系固有频率的比值等有关。当阻尼系数一定时，振动扭矩的振幅仅与轴系的固有频率有关，即与联轴器的刚度有关。

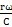
以下分几种不同的扰动扭矩变化频率与轴系固有频率的比值，分析对振动扭矩振动的影响。为了简便起见，不计阻尼系数，即 项等于零。

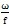
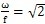
(l）当 =0,或 ，动力放大系数K_d总大于1。

这表示经联轴器的振动扭矩没有放大，前一种情况相当于没有扰动扭矩，或者可认为轴系的固有频率为无限大，即联轴器为绝对刚性体，其刚度C无限大。后一种情况表示联轴器具有一定的刚度，轴系的固有频率与扰动扭矩的变化频率的比值刚好为 。

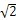
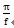
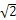
(2）当0＜ ＜ 时，动力放大系数K_d总大于1。

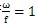
表示在该扰动扭矩的变化频率下，联轴器的刚度还太大，而弹性不够，不能起到减振的作用，以致使经联轴器传递的振动扭矩增大。若 ，则K_d=∞,这表明经过联轴器传递振动扭矩的振幅达到无限大，也就是说，轴系发生扭转共振。此时如有阻尼存在，则动力放大系数为K_d=

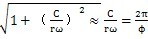
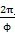
即不会使扭转振动的振幅无限增大。但是通常 都是大于1，因此即使有阻尼，扭振还是存在，阻尼对传动系统的影响程度，完全取决阻尼系数的大小。
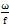
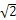
(3）当 ＞ 时，动力放大系数K_d＜1。
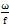
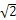
表示只有在固有频率为扰动扭矩的变化频率的万倍时，弹性联轴器才能起到减振的效果。频率比值 >> ，意即采用刚度很小的弹性联轴器，这样动力放大系数可降到很小值，这对减振的效果最好，但是却过分降低了联轴器的承载能力。此外当比值过分大时，也有可能与较高一阶的共振频率接近，仍会引起共振。因此，联轴器的刚度也不宜过分小。

3.3冲击载荷作用下的动力特性
机械可能受到周期性的扰动扭矩作用而引起轴系振动，也可受非周期性的扰动扭矩作用而引起轴系振动。例如有冲击载荷引起的轴系振动。在许多机械上，比较常见的是冲击式作用的变载荷。对于从动轴上作用有常量冲击载荷的情况，与前述情况相似，仍可通过根据冲击载荷条件列出的运动方程，得到在常量冲击载荷作用下的物阻尼系统。有冲击载荷产生的扭转角为：

上式表明轴系有冲击载荷作用时，经联轴器传递振动扭矩的大小，除与转动惯量有关外，还与冲击载荷作用的时间长短有关。以下为按冲击载荷作用时间的长、短的两种情况：
1.冲击载荷突然作用后，在长时间内保持不变，这样的承载方式相当于机械先空载起动，然后在满载条件下工作。此时经联轴器传递的总扭矩为

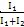
T₁=T₀+ T_d2（1-cosft）                           （3-9）

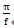
式中T₀经联轴器传递的稳定扭矩，T_d2表示作用在从动轴上的冲击扭矩，当t= 时，经联轴器传递的扭矩达到最大值：

上式表明，如果发生冲击扭矩一侧轴上的转动惯量较小，经联轴器传递的扭矩接近于冲击扭矩的2倍，联轴器的振动周期T为：

在冲击载荷作用下，联轴器的弹性高低，对冲击载荷引起，经联轴器传递最大扭矩的幅值并无影响。只是改变振动周期的长短。联轴器的弹性愈高，固有频率愈低，经联轴器传递的扭矩达到最大值的时间就愈长。因此，联轴器的弹性对改善传递扭矩的平稳性有利。影响联轴器传递的扭矩最大值的因素之一，就是联轴器两侧转动惯量的比值。当冲击载荷作用一侧轴系的转动惯量大于另一侧轴系的转动惯量时，就能减小经联轴器传递的振动扭矩值。此外，当联轴器具有阻尼时，由于阻尼消耗了一部分冲击能量，也可减小最大扭矩。
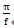
2.冲击载荷突然增加后，只持续一段较短的时间t，就恢复正常值。当冲击载荷持续作用的时间t₁≥ ，即持续时间大于或等于固有频率

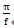
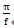
的周期的一半时，经联轴器传递的扭矩仍然有时间达到最大值。因此，这种短时受冲击载荷与冲击载荷增加后在较长时间内保持不变的情况一样，在0＜t<t₁这一时间内，经联轴器传递的扭矩，当不计阻尼时，仍可用（3-1）计算。只有当冲击载荷作用时间t₁< ，才是属于突然的短时间受冲击载荷。此时经联轴器传递的振动扭矩仍可按上述方法得出有关计算式。

当时间区间为O≤t≤t₁时（即冲击载荷开始作用至消失时的时间）由冲击载荷引起的两半联轴器的相对扭转角为：

这与（3-9）相同，对于t≥t₁,即在冲击载荷消失之后的某一时刻，以上两式转化成

如下形式：
因冲击载荷引起的两半联轴器相对扭转角：

由式（3-10）可知，在短时冲击载荷作用下，联轴器传递的最大扭矩随t₁与f之间的关系而变。例如

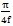
由此可见，随着冲击载荷作用时间的缩短，经联轴器传递的最大扭矩也随着减小。或者在冲击载荷作用时间相同的条件下，只要所选联轴器的弹性相当大，使得轴系的固有振动频率降低以达到保持> t₁，就能使经联轴器传递的最大变动扭矩小于冲击扭矩。综上所述，有冲击载荷作用时，选择具有弹性的联轴器，能够起到缓冲作用。需要多高的弹性，则与冲击载荷持续作用的时间、轴系的转动惯量等有关。一般联轴器的承载能力，随着弹性的增加而降低。因此，对于大型的和需要量较多的联轴器，如果按上述方法选定联轴器，则其尺寸和重量都有加大，从而增加制造成本并增加轴系的附加载荷。为此，当冲击载荷作用次数不多时，可以采用安全性联轴器，或采用具有较高阻尼的弹性联轴器。

3.4不对中时的运动及动态特性
实际上可以将不对中分为冷态不对中和热态不对中两种情况。其中冷态不对中主要是指在室温下由于安装误差造成的对中不良；热态不对中指联轴器在运行过程中由于温度等因素造成的不对中。其主要原因有：转子各零部件受热不均，使联轴器产生热膨胀变形和扭曲变形；发动机热膨胀时由于表面的摩擦力及导向键磨损引起轴承座倾斜和侧行；由于转子的饶性和重量分配不均匀，转子在安装之后产生原始弯曲，进而影响对中情况。

3.4.1不对中时的运动分析

（1）当转子轴线存在轴向的位移时（如图3.2），轴向位移只会产生附加的周向应力，而不会影响转子的运动性。所以这里不进行计算。

（2）当转子轴线之间存在径向位移时（如图3.3所示），联轴器的中间套齿与半联轴器组成移动副，不能相对转动，但是中间套齿与半联轴器产生相对滑动而作平面圆周运动，即中间套齿的中心是沿着以径向位移△y为直径作圆周运动，如图3.4所示。

设A为主动转子的轴心投影，B为从动转子的轴心投影，K为中心齿套的轴心，那么有AK丄BK，设AB长度为D，K点的坐标为K（x，y），取θ为自变量，如图3.5所示。则有

则K的线速度为

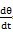
由于中间套齿平面运动的角速度等于转轴的角速度，即 =ω，所以K点绕圆周中心运动的速度为

由上式可知，K点的转动为转子转动的角速度的两倍，因此当转子高速运动时，就会产生很大的离心力，激励转子产生径向振动，其振动频率为转子工频的两倍。

（3）当转子轴线之间存在偏角位移时（如图3.6），从动转子的角速度与主动转子角速度是不同的，从动转子的角速度为

式中ω₁，ω₂——分另为主动转子和从动转子的角速度

a——从动转子的偏斜角

ф₁——主动转子的转角

当主动转子的回转角速度为常数时，从动转子的角速度是偏角和主动转子转角的函数。当或ф₁=0⁰或180⁰时，ω₂最大，当ф₂=90⁰获270⁰时，ω₂最小。其转速比变化曲线如图3.8所示，即有ω₁cosa≤ω₂≤

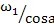
由此可知，当发动机或机组的转子轴线发生偏角位移时，其传动比不仅随转子每转一周变动两次，而且其变动的幅度虽偏角的增加而增大，因而从动转子由于传动比变化所产生的角加速度激励转子而发生振动，其径向振动频率也为转子工频的两倍。

(4）实际旋转机械的转子联轴器处既有平行不对中，又有偏角不对中，即为两种情况的综合，因而转子发生径向振动的频谱特征是两者综合的结果，其径向振动频率为转子工频的两倍。
3.4.2不对中时的动态特性
由上面的运动分析可知，轴向不对中时对联轴器的运动情况可以忽略。所以动态特性分析也只考虑平行不对中、偏角不对中以及平行偏角不对中三种情况。
联轴器连接的两转子轴线之间发生不对中故障时具有平行位移或角度位移，在运动传递过程中，联轴器中间齿套的运动必须同时满足两半联轴器的需要，即中间齿套轴线作平面运动，且轴心线的回转运动频率与转子的运行频率不一致。当产生平行不对中、偏角不对中和平行偏角不对中三种情况时，联轴器中间齿套的轴线回转轨迹分别为图下图所示的圆柱体、双锥体和半双锥体。在这些图中，O₁，O₂为两半联轴器的轴心，O，O′为联轴器中间套齿的静态和动态回转中心，△y，△a分别为转子系统的平行和偏角不对中量。

对于上面图中所示的三种情况，任意回转轮廓的截面图为一周，如图3.12所示，O′的运动轨迹可以描述为

X=△Esin（Ω′t-Ψ）                                         （3-24）

式中Ω——转子的回转角频率

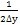
△E——当量不对中量，△E= （平行不对中时）；

 

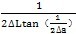
△E= （偏角不对中时）

Ψ——初始相位角，Ψ=2ф（平行不对中时）；

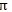
Ψ=2ф（偏角不对中时左端）；Ψ=2ф- （偏角不对中时右端）中间套齿对转子系统施加的激振力为

F_x=4M△EΩ²sin（Ωt-ф），F_y=4M△EΩ²cos2（Ωt-ф）                    （3-24）

工作状态下联轴器的动态特性如图3.13所示，两半联轴器的中心为O₁和O₂，联轴器外壳的动态中心为O′，当系统以Ω转动时，外壳重心的加速度在

其中△e=OO′为系统当量不对中量，在转轴的弹性力的作用下，由质心运动定理：m ₀=-kX，m ₀-kY，考虑到外阻力的作用

现在对结果进行讨论：
(1）当r趋近于O时，动力放大系数M趋近于O；θ趋近于O，这表明，系统在转速较低时，其向应振幅较小，且有较小的相位角。
(2）当r=1/2时，系统发生共振，系统具有振幅最大值，该值的大小只与阻尼系数有关，与此同时，相位角为 。
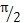
(3）当r趋近于∞时，动力放大系数M趋近去1，这表明，系统在转速较高时，其向应振幅趋于稳定。振幅并不随激振力的迅速增加而加大，与此同时，相位角θ趋近于π，并逐渐保持稳定。
3.5本章小结
本章通过引入联轴器的刚度和阻尼，计算了弹性联轴器在周期性载荷与冲击载荷二的动力特性。在第四节中着重分析了平行不对中，偏角不对中以及平行偏角不对中的运动与动力特性。
从各种不对中的运动学和动力学分析可以得出如下结论：
(1）激励力幅与不对中量成正比，随不对中量的增加，激励力幅则线性加大

(2）在不对中情况下，中间圆环的轴芯线相对于联轴器的轴心线产生相对运动，其中，平行不对中的回转轮廓为一圆柱体，偏角不对中时为一双锥体，平行偏角不对中时为半双锥体。回转体的范围由不对中量决定。
(3）联轴器处于工作状态时，无论是哪一种不对中形式，系统的响应在转速达到临界转速的一半时发生共振，振幅具有最大值。同时，相位角为
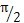
(4）系统在转速大于临界转速后，随转速的增加，其响应振幅趋于稳定，并不随激励力的迅速增加而增大。