不对中状态的理论分析

4.1以材料力学为基础的受扭分析

联轴器正常工作情况下，只受到一个旋转的扭矩。因此首先来研究圆环受扭转时的应力，这要综合研究几何、物理和静力等三方面的关系。

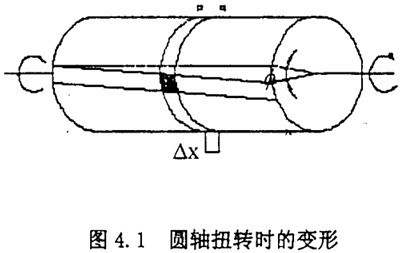
4.1.1变形几何关系
为了观察圆轴的扭转变形，与薄璧圆筒受扭一样，在圆周表面上作圆周线和纵向线，在扭转力偶矩m作用下，得到与薄璧圆筒受扭时相似的现象。即：各圆周线绕轴线相对地旋转了一个角度，但大小，形状和相邻圆周线的距离不变，在校变形的情况下，纵向线仍然近似地是一条直线。只是倾斜了一个微小的角度，变形前表面上的方格，变形后错动成菱形。
根据观察到的现象，做下述基本假设：圆周扭转变形前原为平面的横截面，变形后仍保持平面，形状和大小不变，半径仍保持为直线；且相邻两截面间的距离不变。这就是圆周扭转的平面假设。按照这一假设，扭转变形中，圆轴的横截面就像刚性平面一样，绕轴线旋转了个角度。以平面假设为基础到处的应力和变形计算公式，符合试验结果，且与弹性力学一致。
在图4.1中，ф表示圆周两端截面的相对转角，称为扭转角。扭转角用弧度来度量。用相邻的横截面p-p和q-q从轴中取出长为dx的微段。剪应变

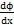
y=P                                            （4-1）

式中dф／dx是转角中沿x轴的变化夔。对一个给定的截面来说，它是常量。公式表明，横截面上任一点的剪应变与该点到圆心的距离p成正比。
4.1.2物理关系
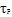
以 表示横截面上距圆心为p出的剪应力，由剪切胡克定律知道

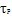
=G·y                                         （4-2）

将式（5-1）代入上式则可以得到

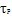
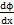
= G·P                                       （4-3）

这表明，横截面上任一点的剪应力 _P与该点到原新的距离P成正比。因为Y_P发生于垂直于半径的平面内，所以Y_P也与半径垂直。如果注意到剪应力互等定理，则在纵向截面和模截面上，沿半径剪应力的分布如图4.2所示

    

因为公式中的 dф／dx尚未求出，所以仍不能用它计算剪应力，这就要用静力关系来解决。

4.1.3静力关系

于圆轴横截面内，按极坐标取微分面积dO，求出内力系对圆心的力矩就是截面上的扭矩即：

  

Ip称为横截面对圆心点的极惯性矩。由公式可以算出横截面上距圆心为p的任一点的剪应力为：

   

在圆截面边缘上，p为最大值R，得到最大剪应力为：

        

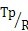
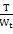
引用记号W_t= ，W_t为抗扭截面系数，便可以改写公式为τ_mox= ，导出的公式中引进了截面极惯性矩和抗扭截面系数，在空心轴的情况下有

  

其中D和d分别为空心圆截面的外径和内径，R为外半径，a=d/D

最后建立圆轴扭转的强度条件，根据轴的受力情况或扭矩图，求出最大扭矩T_max。对于等截面杆，按照公式算出最大剪应力τ_max不超过许用应力[τ]，

4.2以弹塑性力学为基础的受扭分析

在材料力学中已知圆轴扭转时的变形规律。随着扭矩M_T的增加，剪应力也不断增大。由于圆轴最多层剪应力最大，因而最外层首先进入塑性状态，此时的扭矩就是圆轴的弹性极限扭矩

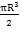
M_T= （τ_θz）_max                                     （4-11）

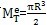
（1）当最外层开始屈服时，此时最外层剪应力应达到剪切屈服应力τ_y，即（τ_θz）_max=τ_y，如图4.4（a），于是有 τ_y。

若选用Mises屈服准则，则有

若选用Tresca屈服准则，则有

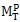
（2）当圆轴整个截面都进入塑性状态，如图4.4（c），此时的扭矩就是圆轴的塑性极限 ，即

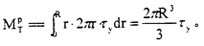
若选用Mises屈服准则，则

若选用Tresca屈服准则，则

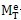
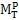
（3）当扭矩M_T处于弹性与塑性极限扭矩之间时，即 <M_T< 时，则圆轴外层处于塑性状态，内层处于弹性状态，弹性区与塑性区的分界面半径为r_P,此时扭矩

此时剪应力在截面上沿半径R的分布情况见如图4.4（b）所示。

若先Mises屈服准则，则有

若选用Tresca屈服准则，则有

随着扭矩的增加，塑料性区由圆轴的外层向轴的中心逐渐扩大，直至整个截面全部进入塑性状态。当轴的整个截面全部进入塑性状态后，圆轴将进入无约束的塑性变形，此时的圆轴将完全丧失承载能力。

弹性与塑性极限扭矩之比为：

4.3轴向不对中时的联轴器的工作状态

在像胶右端面圆环上取单元体，且在分析过程中时取关键的四个象限点的位置作为研究对象，分别为90°，180°，270°，360°位置为研究对象。后面的径向不对中、角向不对中以及综合不对中也采用相同的4个位置进行分析。

轴向不对中时，由于轴向的偏移，橡胶圆环左端面受到附加，的向左拉应力，右端面则受到附加的向右的拉应力，并且在旋转过程中，拉应力σ_ax的大小和方向的大小和方向都不会随着圆环的旋转角度改变而改变；由橡胶圆环旋转扭矩产生的剪应力τ_rot方向始终与其线速度方向相反，而线速度方向在旋转一周的过程中不断的变化。轴向不对中时的应力情况应该是σ_ox与τ_rot的叠加，所以其受力情况比较复杂。
根据实际情况计算出工作时的剪应力：GK2型内燃机车启动发电机ZQF-38TH,115V,38KW,1170～358Or/min；GK2型内燃机机用柴油机型号为MTU16V396TC14，持续功率为1378KW，旋转角速度为18O0rod/min。柴油机冷区液温度为40℃时最小启动转矩包括加速余量约8OON.m，曲轴扭矩约75ON.m

根据联轴器破坏时的橡胶圆环的裂纹方向和角度，可以知道裂纹有一个40⁰的斜角，也就是说引起破坏的应力平面具有一定的角度。首先假设破坏仅仅是源于轴向不对中应起的，下面对具体的位置进行讨论。

（1）轴向不对中90°位置：当圆环上的单元体旋转到最上方时，也就是90°位置时，单元体的应力如下图所示。

此时的受力情况其实属于二向应力状态，利用解析法可知

最大主应力平面如图4.9所示。

（2）轴向不对中180°位置：当圆环上的单元体旋转到最左端时，也就是180°位置时，单元体的应力如下图所示

此时的受力情况仍然属于二向应力状态，只是分析的平面沿着跟着旋转了90°，得出最大、最小主应力为

此时主平面上的正应力平面的角度有这种关系，即a₂较a₁逆时针旋转了90°

（3）轴向不对中270°位置：当圆环上的单元体旋转到最下方时，也就是270°位置时，单元体的应力如下图所示

此时的受力情况仍然属于二向应力状态，只是分析的平面跟着旋转了90°，

此时主平面上的正应力平面的角度有这种关系，即a₃较a₂逆时针旋转了90°

（4）轴向不对中360°位置：当圆环上的单元体旋转到最右端时，也就是360°位置时，单元体的应力如下图所示

此时的受力情况仍然属于二向应力状态，

只是分析的平面跟着再旋转了90°，此时主平面上的正应力平面的角度有这种关系，即a₄较a₃旋转了90°

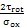
tg2o₄=-                                                     （4-27）

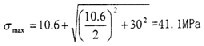
由上面的分析可知，在轴向不对中时，联轴器受到的最大应力的大小始终不变， 大应力方向随着旋转角度变化。

4.4径向不对中时的联轴器的工作状态
径向不对中时，由于径向的偏移，橡胶圆环左端面受到附加的向下的剪应力，右端面受到附加的向上的剪应力，并且在旋转过程中，剪应力τ_rad的大小和方向都不会随着圆环的旋转角度改变而改变；由橡胶圆环旋转扭矩产生的剪应力τ_rot，方向始终与其线速度方向相反，而线速度方向在旋转一周的过程中不断的变化，径向不对中时的应力情况应该是τ_rad与τ_rot，的叠加。所以其受力情况比较复杂。同样取径向位移的方向为y轴，与径向位移垂直的方向为x轴，建立坐标系。分别取四个象限点的位置状态作为研究重点，分别对单元体进行应力分析。

（1）径向不对中90°位置时，这时由，单元体的应力如下图所示

此时的应力属于空间应力状态分析，变形体中任何一点处的应力在不同方向的平面上有不同的值。所谓应力状态指的是任意一点处的应力的大小和方向以及不同平面上应力间的关系。在主平面上，只有正应力，而剪应力分量等于零。主平面上的正应力叫做主应力。由代数理论可知，有以下方程
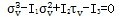
                                     （4-28）

该方程有三个实根，分别为σ₁，σ₂，σ₃，且有σ₁≥σ₂≥σ₃，此三个应力即为分别作用于三个相互垂直平面上的主应力值，并且在此三个平面上无剪切应力。当坐标变换时，虽然每个应力分量都随之改变，但是有些量是不变的，I_l，I₂，I₃分别为第一，第二，第三应力不变量。

σ_zx=τ_rod分别代入（4-29）（4-30）（4-31），得到具体的三个不变量的值

由式（4-35）可知，最大应力平面刚好在垂直于正弦矢量相加的方向。

当τ_rot=10MPo时，可以算出σ_max=σ₁=

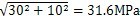
（2）径向不对中180°位置：当圆环上的单元体旋转到最左端时，也就是180°位置时，单元体的应力如下图所示

由图示可知，此时单元体的受力其实是属于纯剪切状态，只是此时的剪切应力为τ_rad与τ_rot的叠加。此时剪应力τ_rad与τ_rot的方向相反。所在最大应力有所抵消。

此时主平面上的正就力平面的角度有这种关系：tg2a₂=-∞，所有a₂=-45⁰或-135⁰

当τ_rot=10MPa时，可以算出σ_max=30-10=20MPa

（3）径向不对中270⁰位置：当圆环上的单元体旋转到最下方时，也就是270⁰位置时，单元体的应力如下图所示

此时的受力由图上可以看出，属于空间应力状态，其基本分析过程类似于径向不对中90⁰状态，现在将径向不对中270⁰时的受力情况：σ_xx=0，σ_yy=0，σ_zz=0，τ_xy=-τ_rot，σ_yz=0，σ_zx=0，σ_zx=τ_rod分别代入式（4-29）（4-30）（4-31），得到

将上述主应力的值代入就可以得知

由式（4-39）可知，最大应力平面刚好在垂直于正弦矢量相加的方向。这与径向不对中90°位置的情况有些相似。

当τ_rot=10MPa时，可以算出σ_max=σ₁=

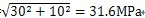
（4）径向不对中360°位置：当圆环上的单元体旋转到最右端时，也就360°位置时，单元体的应力如下图所示

由图示可知，此时单元体的受力其实是属于纯剪切状态，只是此时的剪切应力为τ_rad与τ_rot的方向相同，而在180⁰时方向相反，所以有

此时主平面上的正应力平面的角度有这种关系：tg2a₄=-∞，所以有a₄-45⁰或-135⁰

当τ_rot=10MPa时，可以算出σ_max=30-10=40MPa

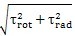
从径向不对中的情况可知，可以知道联轴器的单元体即有三向工作应力状态，又存在纯剪切的工作状态，其最大工作应力大小和方向都随着橡胶圆环的改变而改变。，在旋转一周的过程中，综合考虑四个不同的位置时最大主应力的大小，由于（τ_rot­+τ_rad）>> （τ_rot-τ_rad），所以可以知道最大的最大应力为应该是联轴器360°位置时的最大主应力，最大主应力平面方向与y轴成45⁰夹角。即360⁰位置为径向不对中时的危险点。
4.5角向不对中时的联轴器的工作状态
角向不对中时，由于两轴之间存在一定的夹角，使得橡胶圆环最上方受到附加的拉应力，而圆环的最下端则受到附加的压应力，这个附加的拉应力σ_ang的大小和方向随着圆环的旋转角度改变而改变，在最上方时受拉，且绝对值最大，在最下方受压，绝对值亦最大，所以其变化的过程图形类似于余弦函数；由橡胶圆环旋转扭矩产生的剪应力气．方向始终与其线速度方向相反，而线速度方向在旋转一周的过程中不断的变化。角向不对中时的应力情况应该是。σ_ang与τ_rot­的叠加。所以其受力情况比较复杂。分别取四个象限点的位置状态作为研究重点，分别对单元体进行应力分析。
(1）角向不对中90⁰位置：当圆环上的单元体旋转到最上方时，也就是90⁰位置时，单元体的应力如下图所示

此时的受力情况其实属于二向应力状态，即为拉扭结合，

此时主平面上的正应力平面的角度有这种关系

应力平面如图4.24所示。此时的最大应力值为

（2）角向不对中180°位置：当圆环上的单元体旋转到最左端时，也就是180°位置时，单元体的应力如下图所示

此时的受力图中可以看出，附加的拉应力已经减小为零，实际上单元体受力其实属于纯剪切状态，

此时主平面上的正应力平面的角度有这种关系：tg2a₂=-∞，所以有a₂=-45⁰或-135⁰，最大主应力值为σ_max=30MPa

（3）角向不对中270°位置：当圆环上的单元体旋转到最下方时，也就是270°位置时，单元体的应力如下图所示

此时的受力情况其实属于二向应力状态，只是这时的附加应力变成了压应力。即拉应力变成了负号。利用拉扭结合时的应力分析方程可知

（4）角向不对中360⁰位置：当圆环上的单元体旋转到最右端时，也就是360⁰位置时，单元体的应力如下图所示

此时的受力图中可以看出，附加的拉应力已经减小为零，实际上单元体受力其实属于纯剪切状态，

此时主平面上的正应力平面的角度有这种关系：tg2a₄=-∞，所以有a₄=-45⁰或-135⁰，此时的最大应力值为σ_max=30MPa

通过角向不对中的分析可以知道，具有角向不对中的联轴器受力情况仍然属于两向应力状态，即只有拉扭结合与纯剪切的情况发，没有三向应力状态，比较四个位置的最大主应力

可以知道，在联轴器旋转一周的过程中，最大主应力在90⁰位置。即90⁰位置为角向不对中时的危险点。
4.6综合不对中时的联轴器的工作状态
综合三种不对种情况，对圆环的单元体进行综合受力分析。由于实际工作中联轴器两轴之间不仅存在一定的径向和轴向位移，而且存在一定的偏角。使得橡胶圆环受到附加的轴向拉应力σ_ax，附加的径向剪应τ_rad，附加的角向应力σ_ang，以及由橡胶圆环旋转扭矩产生的剪应力τ_rot。所以综合不对中的应力情况应该是σ_ax、τ_rad、σ_ang与τ_rot的叠加。所以其受力情况比较复杂。仍然按照上面类似的方法分别取四个象限点的位置状态作为研究对象，分别对单元体进行应力分析。
(l）综合不对中位置：当圆环上的单元体旋转到最上方时，也就是90⁰位置时，单元体的应力如下图所示

此时的应力情况属于三向应力状态，所以其分析过程和径向不对中90⁰以及270⁰以情况相似，只是这里还有了附加的轴向拉应力和附加的角向应力，将各个应力值σ_xx=σ_ax+σ_ang，σ_yy=0，σ_zz=0，τ_xy=τ_rot，τ_yz=0，τ_zx=τ_rad分别代入式（4-29）（4-30）（4-31）中，可以得到

I₁=σ_ax+σ_ang+0+0=σ_ax+σ_ang

I₃=0-0-0-0+0=0

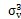
再将三个应力不变量代入方程 - I₁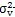 + I₂σ_v- I₃=0中，得到

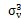
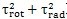
-（σ_ax+σ_ang） -（ ）σ_v=0                            （4-48）

解出这个方程，可以得到三个主应力的值

（2）综合不对中180⁰位置：当圆环上的单元体旋转到最左端时，也就是180⁰位置时，单元体的应力如下图所示

此时的受力仍然属于两向应力状态，因为径向不对中产生的剪应力方向和扭转产生的剪应力的方向在同一平面上而且相互平行。根据计算可以知道

此时主平面上的正应力平面的角度有这种关系

（3）结实合不对中270⁰位置：没圆环上的单元体旋转到最下方时，也就是270⁰位置时，单元体的应力如下图所示

此时的应力情况属于三向应力状态，所以其分析过程和径向不对中90⁰以及270⁰情况相似，只是这里还有了附加的轴向拉应力和附加的角向应力，将各个应力值

将上述主应力的值代入就可以得知

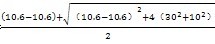
这时取σ_ax=10.6MPa，τ_rad=10MPa，σ_ang=10.6MPa，代入式（4-49）中，可以得出最大主应力为σ_max= =31.6MPa

（4）综合不对中360°位置：当圆环上的单元体旋转到最右端时，也就是360°位置时，单元体的应力如下图所示

此时的受力仍然属于两向应力状态，

此时主平面上的正应力平面的角度有这种关系

这时取σ_ax=10.6MPa，τ_rad=10MPa，代入式（4-56）中，可以得出最大主应力值为

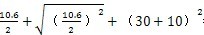
σ_max= =45.65MPa

现在比较一下四个不同位置时的最大主应力的大小

根据上面的分析，可以知道联轴器在综合受力的情况下，其总的应力情况与四个量有关，也就是σ_ax、τ_rad、σ_ang与τ_rot的叠加。为了能够更加形象直观地描述由于不对中量产生的附加应力与总应力的关系，下面进行曲线的拟合。考虑到σ_ax与σ_ang方向都在同一直线上，而τ_rad与τ_rot的方向也在一条直线上，但是这两条直线相互垂直。所以以σ为横坐标轴，τ为纵坐标轴建立坐标系后。各个不对中量都有一个范围，因而由不对中量引的附加应力也有一个范围，

综合以后可知，附加应力的在一个大的矩形里面变化。见图4.39。矩形的方程由下面两式决定：

而在联轴器旋转一周的过程中，各个不对中量都是定值，此时应力范围在见图4.40的椭圆。该椭圆的方程为

4.7本章小结

本章主要从力学的角度对联轴器进行各种不对中的分析。从联轴器各种不对中的分析结果可以得出以下结论。

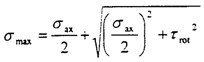
1.在轴向不对中时，在给定的轴向不中量情况下，有最大主应力为 最大应力方向随着旋转角变化。

2.在径向不对中时，在给定的径向不中量情况下，最大主应力为发生在联轴器360°位置，有σ_max=+（τ_rot+τ_rad）。最大主应力平面方向与y轴成45⁰夹角。即360°位置为径向不对中时的危险点。

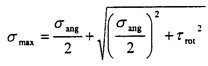
3.在角向不对中时，在给定的角向不中量情况下，最大主应力发生在90⁰位置， 。即90⁰位置为角向不对中时的危险点。

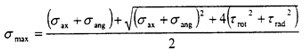
4.在综合不对中时，在给定的轴向、径向和角向不中量的情况下，最大应力为发生在联轴器90°位置，即有 最大危险点在90⁰位置。

随后根据上述结论进行了不对中量范围的讨论。最后得出了用一个大的矩形来表示由于不对中产生的附加应力的范围。矩形的形状由下面的两个式子来决定：

最后根据实际情况的不对中量，绘出了联轴器在旋转一周的过程中最大应力的椭圆。该椭圆的方程为 。
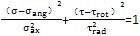