管道开裂射流场的数值模拟
本章利用已有的流场求解程序,通过有限体积法求解气体动力学基本方程。文中对开裂后的高压输气管道气体逸出引起的可压缩高速自由射流流场进行了数值模拟,得到了作用于管壁的分布气体压力和管道内外气流场的特征参数。
本章数学符号独立,与其他章节没有继承关系。
5.1湍流场的数值模拟方法
5.1.1直接数值模拟(DNS)
直接模拟方法即不引入任何湍流模型,通过高精度、低色散、低耗散的差分格式求解完整的非定常N-S方程,对湍流的瞬时运动进行直接的数值模拟。
这种方法的优点是:方程本身是精确的,仅有的误差只是由数值方法引入的误差;数值模拟可以提供每一瞬间所有流动量在流场上的全部信息。
但是,湍流的直接数值模拟一直受到计算机速度和容量的限制。它的难点及存在的问题主要有:计算量十分巨大;流动平均量一般要比扰动量大几个量级。求解时,由于差分格式存在截断误差,从而可能将真实扰动量淹没掉。
理论上,直接数值模拟是射流流场数值模拟最精确的方法,但由于该方法计算量巨大,对计算机的计算能力有很高的要求,目前的计算机性能还不能够满足复杂流动的直接数值模拟的要求,利用直接数值模拟求解射流流场问题还没有见到和实验结果进行比较的文献。
5.1.2大涡模拟(LES)
大涡模拟的基本思想是把包括脉动运动在内的湍流瞬时运动通过某种滤波方法分解成大尺度运动和小尺度运动两个部分。大尺度量要通过数值求解运动微分方程直接计算出来;小尺度运动对大尺度运动的影响将在运动方程中表现为类似雷诺应力一样的应力项,称之为亚格子雷诺应力,它们将通过建立模型来模拟。
大涡模拟的最主要的困难不在于计算机的限制,而是大涡模拟方法本身。例如,现有的亚格子应力模型还很不完善,特别是近壁区内的模型以及边界条件的提法等等都是急待解决的问题。使用该方法进行射流流场的数值模拟也还在探索之中。
5.1.3湍流模型理论
湍流模型理论在射流流场的数值模拟中已经取得了较好的应用,目前人们已经广泛的应用湍流模型理论对射流的流动进行分析,并取得了很大的进展。
所谓的湍流模型理论就是以雷诺平均运动方程为基础,依靠理论与经验的结合,引进一系列模型假设,建立一组描写湍流平均量的封闭方程组的理论计算方法。目前,在射流流场的数值模拟中常用的湍流模型有B-L混合长模型,S-A一方程湍流模型,RNGK-ε方程湍流模型,雷诺应力湍流模型等。
在湍流模型的选择方面:
AndrewT.T.和ChistopherK.W.T.(1996)应用修正的k-ε二方程湍流模型计算了轴对称及方形、椭圆形喷嘴的自由射流,马赫数为0.4~2,计算结果与实验值进行了比较,吻合较好:
EghlimiA.和SahajwallaV.(1999)分别采用了k-ε湍流模型、RNGk-ε湍流模型、Realizek-ε湍流模型和雷诺应力湍流模型对轴对称的亚声速自由射流进行了数值模拟。通过计算值与实验值的比较,可以发现除了标准的k-ε湍流模型对轴对称的亚声速自由射流流场数值模拟的结果与实验值有较大偏差外,采用其他三种湍流模型计算结果与实验值都吻合得比较好;
NASA的ReddyD.R.,SteffenC.J.,ZamanK,B.M.Q.(1999)应用S-A湍流模型对三维方形喷嘴自由射流进行了数值模拟,计算结果表明,在超声速流动下,计算值与实验值吻合较好,在亚声速流动时偏差较大。
5.2 S-A湍流模型
根据流场数值计算领域已有的研究经验,结合本文问题的性质,在大量试算的基础上,本文选择了S-A湍流模型。这一节介绍该模型的原理。
S-A湍流模型是Spalart和Allmaras在1992年提出的一方程湍流模型,具体描述如下:
湍流运动粘性系数
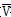
满足输运方程
S-A湍流模型常用于大梯度、近壁的气体流动的数值模拟,在涡轮机械、高速气体流动等方面的计算中有着广泛的应用。
5.3N-S控制方程
非定常可压缩的射流满足如下的积分形式的N-S方程:
上式中,Ω是控制体,
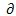
Ω是控制体边界面,W是求解变量,F是无粘通量,G是粘性通量。
式中P为密度,
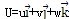
表示速度,E为总能,
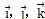
分别为沿x,y,z方向的单位矢量。
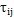
为粘性应力项,
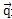
是热通量。
将以上各项写成分量形式:
其中μv是分子粘性系数,μt是湍流粘性系数,Prv是分子普朗特数,Prt是湍流普朗特数。
为了便于粘性通量的计算,采用原始变量
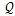
为变量,
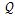
定义为
5.4非结构性网格
相对于结构性网格而言,非结构性网格能够更有效的适应形状不规则、边界弯曲的复杂领域,以及依据不同的分辨率要求,分配求解域内的网格。特别是三角形网格(对于二维问题)和四边形网格(对于三维问题)。
5.4.1非结构性网格的特点
在结构网格中,网格点总是分布在某种坐标变换后的坐标线上,在拓扑上是规范的(个别变换的奇点除外),而非结构性网格则不要求拓扑上的规范性。
非结构性网格的网格点在空间的分布比较自由,不要求每个网格点具有相同数量的邻点,每一个网格点参与构成的单元数量也可以互不相同,网格点之间的连接不再具有方向性。在非结构性网格的划分中没有网格线的概念,因而能够更为有效地适应形状不规则、弯曲边界的复杂领域,以及依据不同的分辨率要求,分配求解域内的网格。非结构性网格的划分问题都直接在物理平面(或物理空间)中讨论。
以三角形单元网格为例,互相靠近的不在同一直线上的三个网格点(内点或边界点),均可以相互连接而构成一个计算单元,只要在这个三角形内部以及其边上,没有其他的网格点。
5.4.2非结构性网格的数值求解方法
非结构性网格的数值求解方法通常必须采用有限体积法建立差分方程。
有限体积法是介于有限差分法和有限元法之间的一种计算方法,它针对一个有限体积的单元体,通过差分离散建立差分方程。由于非结构性网格的网格划分更接近于有限元的网格划分思想,直接采用微分方程出发的差分方法很不方便,而必须采用从积分型方程出发。本文5.5节有详细的介绍。
5.4.3非结构性网格的生成
非结构性网格的生成大致可分为两大类:两步法和一步法。
两步法就是将非结构性网格的生成分为两个步骤完成,第一步是在求解域内生成网格点:第二步是把边界上的网格点和内部已生成的网格点,连接成合适的三角形网格划分;
一步法则把网格点的生成与三角形单元的形成统筹考虑,在生成网格点的同时考虑连接关系,而在考虑三角形的连接时,又同时考虑网格点的增删,这类工作的代表是Delaunay方法。对于三角形网格单元,每个三角形越接近于正三角形时,网格的素质越好。
本文中的非结构性网格的生成是通过网格生成软件包GAMBIT来实现的,采用的是Delaunay方法。
5.5有限体积法求解过程
采用有限体积法,控制体选取为网格单元,将物理量置于网格单元中心,如图5-1所示。
对方程(5-10)在单元i上积分,有
(5-14)式中,nb(i)表示单元i的相邻单元数,下标“i,j'”表示单元i和单元j的交界面,
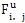
表示界面(i,j)处的无粘通量,
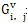
表示界面(i,j)处的粘性通量,
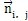
表示界面(i,j)的外法线单位矢量。
在三维的情况下,V
i为单元i的体积,A
i,j为界面(i,j)面积:在二维的情况下,V
i为单元i面积,A
i,j为界线(i,j)长度;Γ
i表示单元i的Jacobian矩阵Γ。
5.5.1无粘通量
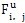
的确定
确定无粘通量只愁的方法较多,大体上可以分成两大类。
一类是中心型格式,这类格式需要加入人工粘性来抑制间断附近的非物理振荡,因此,对于这类格式必须较好的控制人工粘性系数,这带有相当大的人为性,并且难于找到普适的人工粘性系数,因此很不方便;
另一类是迎风型格式,应用的较为广泛的有TVD,ENO和NND等格式。非结构性网格上的TVD和ENO格式在求解Euler方程的时候,取得了较大的成功,但在粘性流体计算中需要借助于网格单元中与控制面相对的顶点值,因而对网格的依赖性较大,要求网格的均匀性较好。
然而,在粘流的计算中,出于分辨边界层的需要,网格在壁面法线方向相当密集。在现有的计算条件下,采用均匀网格是做不到的。NND格式和基于Roe矢通量差分分裂的迎风格式,只借助于控制面两侧单元中心点值,因而对网格均匀性的要求有所减弱。本文采用基于Roe矢通量差分分裂的迎风格式。计算无粘通量的时候,采用Roe矢通量差分分裂,有
ε为略大于零的数,一般取ε=0.05aM。
A1由下式计算:A1=|UM|,A2,3=|UM±aM|。
这样,无粘通量
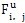
的确定就转化成了
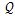 L
L和
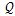 R
R的确定。若取
便可方便的得出一阶精度格式。显然,一阶精度格式对于粘流的计算来说是没有应用价值的。为了构造高精度格式,必须寻求确定
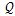 L
L和
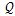 R
R的高精度方法。对于二阶精度格式,
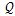 L
L和
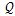 R
R的表达式可由下式确定:
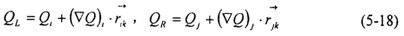
其中,(▽
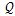
)
i和(▽
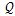
)
j,分别为Q在单元i和j内的梯度;k为界面(i,j)的中心,
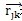
表示单元j中心到k的距离矢量,
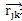
表示单元i中心到k的距离矢量。将(5-18)代入(5-16),即可得到无粘通量
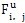
。可以证明,这样确定的
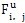
具有二阶精度。
在(5-18)式,我们用到了原始变量的梯度(▽
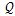
)
i和(▽
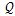
)
j。在非结构网格中,物理量的梯度可以由高斯积分公式求得。令ф代表任一变量,则
其中,Ω为积分路径构成的封闭体,
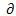
Ω为该封闭体的边界面,
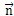
为边界面上的
外法线单位矢量。原则上积分路线可以任意选择,只要包围计算点即可。
以二维情况为例,计算图5-1中A点梯度可选C→B→D→C作为积分路径,但为了保证积分的精度,最好使积分路径构成的封闭体形心与计算点重合,或至少比较接近。
但是,由(5-18)直接得到的格式在激波附近是不稳定的,将会出现非物理振荡。迎风格式通过限制物理量的梯度值,来保证物理量在单元内的分布具有单调性,从而达到抑制间断附近非物理振荡的目的。这时,(5-18)式变为
5.5.2粘性通量
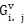
的确定
粘性通量
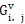
由控制面上的速度、压力及密度的梯度项组成,所以粘性通量
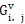
的计算主要是求出控制面上相关物理量的梯度值。首先由(5-19)式求出各单元内物理量ф的梯度值后,界面(i,j)上物理量的梯度值可简单地由相邻单元内物理量ф的梯度值的算术平均得出:
5.5.3离散方程的求解
在计算出无粘通量
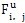
和粘性通量
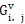
后,代入(5-14)式可得到半离散的差分方程:
方程(5-24)可以采用显式或隐式的方法进行求解。但是由于受时间步长的限制,采用显式的R-K时间推进方法需要迭代的步数较多,计算很不经济,因此本文采用了Gauss-Seidel迭代隐式求解的方法。
式(5-24)在时间方向采用Euler后向差分,有
对方程(5-25),采用Gauss-Seidel点迭代法隐式求解。
5.5.4边界条件
在边界处理方面,采用传统的边界处理方法。
1.计算域的入口采用入流条件,亚声速时给定总压、总温和速度的方向,其他参数值由内点外推;超声速时给定边界上的所有参数值。
2.计算域的出口采用出流条件,亚声速的时候在出口截面上给定环境压力,其他参数值由内点外推,超声速出流边界不提任何条件;
3.对称轴处采用轴对称条件,对称轴上法向速度为O,其他参数值一阶偏导为O;
4.固壁采用无滑移固壁条件,u=v=w=O;
5.人工边界用无反射边界条件。
其中无反射边界条件是根据特征线的方法来求出边界上的参数值。根据一维完全气体无粘非定常运动的方程组,在亚声速的条件下由边界上的入射波和出射波关系可以得到两个Riemann不变量:
其中Vn为沿边界法向的速度分量,c为当地声速,下标∞表示无穷远处的参数值,下标i表示计算域内紧邻边界的点的参数值。
无穷远处的参数值为已知,计算域内的参数值可以通过内点的计算得出,因此我们可以得到边界上的沿边界法向方向的速度分量和当地的声速值:
边界上的沿边界切向方向的速度分量和熵的值可以通过内点外推得到。
5.6结果分析
图5-2是第二章稳态裂纹扩展计算得到的管道壁道面在某上瞬时的变形状态。
图5-3是以图5-2为依据建立的流场计算网格。设计参数为:裂纹扩展速度200m/s,管道外径1016mm,壁厚14.7mm,内压10MPa。
外部流场区域选取范围为3m×5m。输送介质选用天然气的主要成分甲烷,初始外流场设定为空气。远场压力定义为大气压。在底部和侧面应用对称边界条件。计算段管道全长为35m,裂尖位于距轴向对称面18.88m处。管壁的扩张速度按照第二章的计算结果作为流场的运动壁面边界条件。
计算的结果揭示了一些重要的现象。
图5-4给出了XZ对称面上的马赫数分布。管道中的流动在裂尖出口处达到超声速,而在对称面附近发生了强烈的回流。标示为B的位置压力和密度发生了强间断,意味着出现了激波。
为了进一步观察XY截面上的速度,图5-5绘出了图5-4中标示的A-A截面的速度分布。
矢量箭头表示的是X-Y面内速度分量的方向,等值线表示三维流动区域中的速率大小。从图上可以看出外部流场的速度分布沿Y方向从中心到两侧速度迅速降低。在距管道中心五倍远的外流场,气流速度仍可达到671m/s。
图5-5右侧的放大截面上标出了A至E的五个点。保持各点的X坐标不变,变化Z坐标,可在管壁上分别划出对应于截面上不同位置的轴线。
由于管道内壁处的气体静压等于该处管道承受的压力,图5-6和图5-7中A-E各点沿Z向的气体静压变化反映了管道承受压力的轴向衰减规律。两图中的初始内压分别为10MPa和8MPa。
与线性衰减模式(2-47)(某估算结果在图5-6中用点划线标出)相比,计算得到的静压衰减结果揭示了几个重要问题。
其一是回流区的发现。在轴向两侧扩展裂纹的对称面附近发现了强烈的回流,这在裂纹扩展初期将导致管壁的裂纹后端的抖动,从而对裂纹驱动力起到重要影响。随着裂尖位置的不断前移,回流区的压力将逐渐衰减到大气压值。
其二是回流区的位置。计算表明,回流区宽度随管道工作压力的升高而增长,随裂尖位置的前移而减小。
其三是衰减区的压力变化。气流通过裂纹尖端时,管壁上作用的气体压力沿轴向迅速衰减,经验公式(2-47)中所用的衰减长度一般取为1.5倍管道直径,最终衰减到零。计算表明衰减长度随管道工作压力的升高而增加,并且衰减区压力的最低值与管道的工作压力相关。由于对裂纹的扩展状态影响甚微,裂尖前部的压力不是关心的对象。
此外,本文计算与公式(2-46)基本相符,这和全尺寸爆裂实验得到的结果是一致的。在(2-46)的基础上,本文提出以下的修正压力衰减模式以替代(2-47)进
通过多种工况验证,该模式与计算结果吻合良好。
另外,通过和意大利CSM的实测管理压力曲线图5-8相比较,证明图5-6和图5-7从趋势上是成立的。
5.7本章小结
本章以有限体积法为基础,对非定常可压缩的Navier-Stokes方程进行了离散和求解。网格的划分采用非结构性网格,无粘通量采用Roe矢通量分裂,差分格式为二阶精度,时间离散采用Guass-Seidel隐式迭代,在人工边界上采用基于特征线法的无反射边界条件。
对含动态裂纹的高压输气管道的流场模拟结果表明,气体压力模式(2-46)和(2-47)式在裂纹充分发展至不考虑回流区影响的条件下,对高压高韧性管道仍然成立
回流区的发现对裂纹开始扩展不久的一段时间内的裂纹驱动力起重要影响,对于判定止裂点的位置有着重要的工程意义。(5-29)和(5-30)式可直接应用于有限元程序以提高裂纹扩展与止裂的模拟精度。