三叉杆式万向联轴器的理论运动分析

3.1前言

三叉杆式万向联轴器是一种新型的万向联轴器，它在结构上简单、紧凑、安装方便，具有承载能力大和工作可靠等优点。在国外已广泛地被应用于汽车工业和其它的工业领域。但由于它的运动规律复杂，为了彻底弄清它的特点，长期以来一直都有人对它运用不同的计算方法进行运动分析。本章运用方向余弦矩阵这一数学工具，对三叉杆滑移式万向联轴器运动机理进行解析计算，得出它的运动规律表达式和曲线图，并在后面的章节中运用同样的结构进行仿真验证，以检验计算的正确性。

3.2三叉杆式万向联轴器的理论运动分析

3.2.1三叉杆滑移式万向联轴器简介
三叉杆滑移式万向联轴器由滑杆套轴（又称为输入轴）、三叉杆（又称为输出轴）、小杆和内球头等组成产（这几个构件的模型图3-1所示），其中小杆和内球头装配成滑杆（模型的装配关系如图3-l最上部），在这种连接形式下，内球头可在小杆内转动，即形成球面副，具有三个转动自由度。在滑杆套轴上有三个均匀分布的孔（小杆的滑道），与安装在三叉杆轴颈上的滑杆相配合，这里所有的配合均为间隙配合。当三叉杆万向联轴器运转时（两轴有夹角），滑杆一方面沿滑道的中心线移动，另一方面沿三叉杆轴颈移动，从而实现运动过程中的角度补偿。

3.2.2分析模型的建立
由于运动规律的特殊性，为了实现它的运动，对单联的三叉杆式万向联轴器需要在输出轴上安装调心轴承（调心轴承的模型装配关系如图3-1所示，它的内圈同三叉杆无相对滑动），否则它在理论上是不可以转动的（自由度不够）。再装上机架，即左支承（如图3-1)，就构成了三叉杆滑移式万向联轴器的装配模型。其模型如图3-2所示。

通过对图3-2中的模型进行抽象，可得到三叉杆滑移式万向联轴器的机构运动简图，其示意图如图3-3所示，在此模型中关节轴承中心同三叉杆三轴颈轴线的交点距离一直不变。由以前的分析可知，在这种模型中，三叉杆中心的运动轨迹在输出轴平行于自身运动时是以

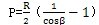
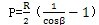
为半径的圆，其中R为输入轴滑道轴线至。输入轴轴线的距离（图3-4中有其示意），β为输入、输出两轴线之间的夹角（图3-5中有其示意）,L为圆锥摆中轴线长。所以采用调心轴承安装输出轴时，输出轴的运动必为一圆锥摆运动，三叉杆中心的偏心距P比值 有关。当L为无穷大时，,这时相当于用双向心轴承安装输出轴，随着 增大L

P的计算值与实际值将会出现微小的误差；由于误差极小，所以在一般应用场合可以取P≈ （ ）

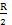
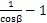
由于在转动的过程中，三叉杆交点作旋转运动，因此会导致输入轴与输出轴之间的夹角发生变化，其变化范围为β_min～β_max，当O点（见图3-5）处于输入轴与输出轴转动锥中心线所构成平面的两个极限位置时，偏转角达到两极值:

在其它位置时，偏转角介于两者之间。

3.2.3坐标系的建立
由于输出轴作一圆锥运动，在分析的过程中需建立三套坐标系，如图3-5所示。
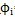
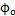
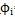
首先建立两个固定坐标系OXYZ和O′X′Y′Z′，输出轴转动锥中心线取为轴OZ，输入轴的轴线取为O′Z′，其中O与O′重为oZ与O′Z′交点，取轴OY与O′Y′重合，且垂直于形成夹角β的OZ和O′Z′两轴所在平面，则坐标系O′X′Y′Z′可看作是坐标系OXYZ绕OY轴旋转一个角度，即为输入与输出之间的夹角β所得。另外，在三叉杆上固连一动坐标系O″X″Y″Z″，原点O″即为三叉杆的交点，O″Z″即为实际输出轴轴线，O″X″Y″平面即为三叉杆所在平面，且取轴O″Y″始终垂直于OX轴（即动坐标系O″X″Y″Z″也随三叉杆作圆锥运动）。假定在初始状态下，导向滑道轴线m₁位于O′X′Z′平面内，三叉杆轴线n₁位于与固定平面OXZ重合的动平面o″X″Z″内，当输入轴转过一角度 时，输出轴上三叉杆转过 角,其中输入轴转过角 时，在坐标系O′X′Y′Z′中位置如图3-4所示（图3-4中右图为左视图，w_i为输入转速），这样建立坐标系后，就可以利用引入齐次坐标的方向余弦矩阵——四阶变换矩阵进行运动方面的分析了。

3.2.4运动分析
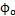
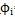
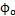
按图3-5所示坐标系，可先在动坐标系O″X″Y″Z″中建立三叉杆轴颈的轴线参数方程然后通过坐标变换转至固定坐标系O′X′Y′Z′中，因输入轴的滑道轴线同三叉杆轴颈的轴线相交（于小杆球面的中心），故在坐标系O′X′Y′Z′中联立三叉杆轴颈的轴线参数方程和输入轴的滑道轴线参数方程，在这个联立的方程中会出现两个未知量即输出转角 和动坐标系中的一个坐标x″，方程数和未知量数是相同的，可以求解，通过消除了即可求得 同 的关系；同时小杆球面的中心在固定坐标系O′X′Y′Z′中的运动轨迹也可求出。

3.2.4.1联立方程的求取
由建立的坐标系可知：
在定坐标系O′X′Y′Z′中输入轴的三滑道轴线m₁、m₂、m₃方程为：

在动坐标系O″X″Y″Z″中三叉杆轴颈的轴线n₁、n₂、n₃方程为：

定坐标系O′X′Y′Z′与定坐标系OXYZ之间的四阶变换矩阵为：

下面讨论如何在固定坐标系O′X′Y′Z′中表达出三叉杆轴线的参数方程。

为求出这个参数方程，我们必须解决动坐标系O″X″Y″Z″同定坐标系OXYZ之间的坐标变换矩阵[Moo″]。

已知O″点在OXYZ中的坐标为：

由于动坐标系O″X″Y″Z″的O″Y″轴取得始终垂直于固定坐标系OX轴，可认为先把OXYZ坐标系绕OX轴转过夹角θ_z，使OY轴与O″Y″轴平行，再绕新的OY轴转过θ_y，使OX轴与O″X″轴平行，OZ轴也同时平行于O″Z″轴（变换空间位置如图3-6所示）。则固定坐标OXYZ与动坐标系间的变换关系如下：

所以有：

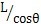
因O″Z″与OZ的交点S在OXYZ坐标系中的坐标为（O，O，L），在O″X″Y″Z″坐标系中的坐标为（O，O ），代入式（3-5）

可推出：

由式（3-6）可知|θ_y|<θ，|θ_x|<θ一般来说θ值非常小，则θ_y和θ_x则更小。到此方向余弦矩阵[Coo″]的所有项均可求出。其具体的形式如下（为简化书写将θ_y作为已知参数代入）：

于是动坐标系O″X″Y″Z″与定坐标系OXYZ之间的四阶变换矩阵[Moo″]为：

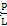
其中tgθ= ，（L为圆锥摆中轴线长，P为圆锥摆底圆半径（见图3-3））

又坐标系O′X′Y′Z′与坐标系O″X″Y″Z″之间的四阶变换矩阵为：

[Mo′o″]=[Mo′o] [Moo″]

故三叉杆轴颈的轴线方程由坐标系O″X″Y″Z″转到坐标系O′X′Y′Z′为：

（3-7）式中A₁、A₂、A₃、A₄、B₁、B₂、B₃、B₄、C₁、C₂、C₃、C₄等于其在矩阵[Mo′o″]中对应位置的表达式。

将式（3-3）同式（3-9）式联立，则有：

3.2.4.2输入、输出转角关系的求取
由式（3-1o）中的（1）、（2）两式，消去x″，即可求出输入角 同输出角 的

关系。
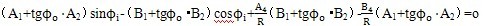
   （3-11）

在式(3-11)中略去sinθ的平方和高次项（根据实际情况p«L，故θ也非常小），同时令cosθ_y≈1（由式（3-6）可知是合理的）。则可得出输入同输出转角关系：
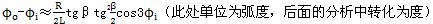
转角关系：   （3-12）
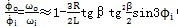
速比关系： （单位为弧度/秒）                       （3-13）

3.2.4.3小杆的运动分析

3.2.4.3.1小杆相对于滑道的运动
对式（3-1o）中的第（3）式作近似处理sinθ≈ ≈o，cosθ≈1（实际上p<<L,近似处理是合理的），则可得到三小杆的球面中心P在固定坐标系o′X′Y′Z′中的运动轨迹：

由式（3-14）则有小杆在滑道中的滑动位移即为坐标z′值，由于三小杆的滑动位移是相同的，可取其中之一进行表示，令h₁为其位移量则可表示为：

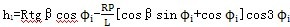
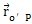
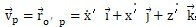
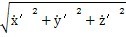
小杆球面中心P在定坐标系o′X′Y′Z′中的坐标（X′Y′Z′）表示成向量形式为： =（x′，y′，z′），将其对时间t求导得到： ，则P点的绝对速度为v_p= 。其中：

 

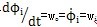
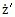
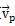
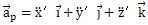
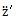
上式中作 的处理（三叉杆式万向联轴器输入同输出的转角差值很小，可以认为是等角速传动，这在后面的分析中可以证明。） =v_pz是小杆沿着滑道的相对速度，将速度 再次对时间t求导可得小杆运动的加速度： （其中 =a_pz是小杆沿着滑道的相对加速度）。
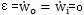
假设输入轴的转速为定值，则，此时：

 

3.2.4.3.2 小杆（球面中心P）相对于三叉杆轴颈的运动小杆的球面中心P在动坐标系O″X″Y″Z″中的参数方程为：

（方程中h_j为小杆的球面中心P到三叉杆轴线的距离，因为三小杆运动相同，故取其中之一分析，可令j=o)
将（3-17)式代入（3-1o）式中第（2）个方程可得
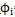
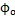
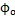
Rsin =B₁h_ocos +B₂h_osin +B₄

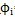
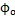
由 = ，cosθ≈1，sinθ≈o则可得出小杆球面中心P沿着三叉杆轴颈相对位移量为：

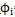
h_o=R-P-2Pcos2                                    （3-18）

将位移h_o对时间t求导可得小杆球面中心P沿三叉杆轴颈的相对速度：

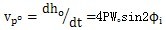
                             （3-19）

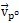
将速度 再次对时间t求导可得小杆球面中心P沿三叉杆轴颈的相对加速度：

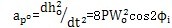
                          （3-2o）

3.2.5结果分析
对我们进一步分析有意义的有如下各量：

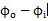
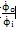
输入、输出转角差值 同输入、输出角速度比值 随输入角和两轴夹角的变化情况；
小杆沿滑道运动的位移h₁、速度v_Pz和加速度a_pz随输入角和两轴夹角的变化情况；
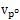
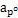
小杆的球面中心P沿三叉杆轴颈运动的位移h_o、速度 和加速度 随输入角和两轴夹角的变化情况；
故绘出它们在不同的轴夹角β下随输入轴转角 的变化曲线图，以便进行直观的分析。

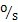
假设R=37mm，L=14o.5mm，ω_i=9o （为了使理论分析结果同仿真试验的结果相互验证，这里的尺寸 和运动参数的选取实际上就是仿真中用到的数字），绘出以上被关注量随输入轴回转两周的曲线图，分别如图3-7、图3-8、图3-9、图3-1o、图3-11、图3-12、图3-13和图3-14所示。

由以上对各曲线图的分析，可以知道三叉杆万向联轴器在一定的程度上可以认为是一种等角速联轴器；它的各个运动参量，一般都随两轴夹角β的增大而增大，有的还变化较大，故不适宜于在大夹角的工况下工作。

3.3本章小结
通过引入在调心轴承安装工况的三叉杆滑移式万向联轴器模型，建立合适的运动模型和坐标系，利用齐次坐标的方向余弦矩阵——四阶变换矩阵，对三叉杆滑移式万向联轴器进行运动分析，得到其各个构件的位移、速度和加速度表达式和变化曲线，并对各曲线进行了分析，得出它是一种准等角速联轴器，为本文后续的仿真验证和以后的动力分析提供了基础。

对曲线图的分析：

由曲线图3-7可以看出两轴的转角差相当小，即使在两轴夹角达到2o^o时，输入同输出的最大转角差也不到o.1^o，所以在一定的程度上认为输入、输出转角相同是有一定的道理的。且转角随两轴夹角β的增大而增大，变化的频率为一个回转周期3次。

由曲线图3-8可以看出，当输入轴转速恒定为9o^o/s时，输出轴的转速变化也是相当的平缓，即使在两轴夹角达到2o°时，其角速度变化的最大值也仅有o.4 ^o／s，所以在一定的程度上可以认为这种联轴器是一种等角速联轴器。角速度的变化频率为一个回转周期3次，在一个回转周期内完全等速点有六次。且角速度差随两轴夹角β的增大而增大。
由曲线图3-9可以看出，小杆沿滑道的位移随两轴夹角β的增大而增大，变化量也比较大，变化频率为一个回转周期1次。这可以作为三叉杆万向联轴器设计中，小杆长度的设计依据。
由曲线图3-1o可以看出，小杆球面中心P沿轴颈位移是以尺寸R为回归中心，随两轴夹角β的增大而增大，不过变化的范围不是很大，在两轴夹角达到2o°时，其变化量也不到5mm，相比小杆沿滑道的位移它的值要小得多。它的变化频率为一个回转周期2次。
由曲线图3-11可以看出，小杆沿滑道的运动速度也具有周期性，它的变化频率为一个回转周期1次。曲线同正弦线有一点相似，但上下不对称，随两轴夹角卢的增大其最大值增长较快，这一数值可以作为动力分析中摩擦计算的重要依据。
由曲线图3-12可以看出，小杆球面中心P沿轴颈的线速度随两轴夹角β的增大其最大值增长也较快，它的变化频率为一个回转周期2次，曲线上下对称这一数值可以作为动力分析中摩擦计算的重要依据。

由曲线图3-13可以看出，小杆沿滑道的运动加速度其变化较为复杂，变化具有周期性，变化频率为一个回转周期1次。随两轴夹角β的增大其最大值增长较快，它的值可以作为动力分析和设计计算的重要依据。
由曲线图3-14可以看出，小杆球面中心P沿轴颈的线加速度，变化频率为一个回转周期2次。随两轴夹角β的增大其最大值增长较快，它的值可以作为动力分析和设计计算的重要依据。