双联三叉杆式万向联轴器的动力仿真

5.1引言
任何机械都有运动，任何机械都受到力的作用，各种机械因受到力的作用而运动，在运动中又会产生力。正是由于力和运动的相互影响，才使动力学问题相当的复杂，这一点在空间机构中体现更是突出。由前面的分析可知，三叉杆式万向联轴器机构是一种运动规律非常复杂的空间机构，它的动力分析自然十分复杂，如用手工去计算几乎不可能。
动力分析是进行机械设计的基础。只有通过动力分析知道物体的受力状况，才可在机械设计中对物体进行强度、刚度、疲劳、寿命等机械性能进行计算。由此，动力分析的重要性可见一斑。
由于动力学研究的复杂性，人们常常引入一些假定，使问题简化。有时这种假定无关紧要，有时则会导致计算的失误。但随着生产实践的发展，对动力学分析的准确度提出了新的要求。如果仍旧采用静态代替动态的静力学方法和恒定动态代替变动动态的动态静力学方法，则根本不能满足分析的要求。为此必须进行真正的动力学分析或弹性动力学分析。
力学理论的发展、电子计算机的改进和广泛应用为动力学分析方法提供了理论基础和实践手段。目前在众多的CAD、CAE软件中，ADAMS以其较强的运动学，动力学分析功能在众多工程领域里获得了广泛的应用，利用它能较好的解决上述的动力学问题。
本章利用ADAMS软件，对第四章中建立的双联三叉杆万向联轴器进行多刚体的动力分析，得到了一些有用的、可视化的结果。

5.2理论背景

5.2.1机械动力学简介
机械动力学研究机械在力作用下的运动和在运动中产生力的科学。由于机械产品的高速化、精密化、轻量化、大功率化的发展趋向不断促使机械动力学的发展，要求提出更精确、更真实的反映客观实际的动力学分析方法而摒弃以前在计算中的许多假设和简化。
在机械动力学发展的过程中产生了如下四种分析方法：
静力学分析（Static Analysis）。对于低速机械，在运动中的惯性力可以忽略不计。在机械运动过程中的各个位置采用静力平衡的方法求解；

动态静力学分析（Kineto-Static Analysis）。随着机械的速度的提高，惯性力不能再被忽略。假定构件按理想的规律运动，利用达朗贝尔原理求解；
动力学分析（Dynalnic Analysis）。由于在各种力的作用下，机械并不能维持理想的运动规律这一假定，在分析中，把原动规包括在机械系统之内来进行分析。
弹性动力学分析（Elasto-dynamics Analysis）。在前三种分析方法中，构件均被假定为刚性的，但随着机械轻量化的发展，构件柔性加大，运转速度提高，惯性急剧增大，在这种情况下，构件的弹性变形会给机械运动的输出带来误差。
机械弹性动力学是机械动力学发展的新阶段，它研究把机械的构件看作是弹性的而不是刚性时的机械运动状态，以及为抑制弹性动力响应而采取的措施和相应的机械设计方法。目前这种方法已得到了广泛的应用。

5.2.2ADAMS中的动力学方程
ADAMS中采用拉格朗日乘子法建立系统动力方程

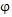
完整约束方程 （q，t）=0
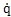
非完整约束方程θ(q， ，t)=0
其中：
T——系统动能；
q——系统广义坐标列阵；
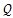
——广义力列阵；
p——对应于完整约束的拉氏乘子列阵；

μ——对应于非完整约束的拉氏乘子列阵；

通过求解此微分方程的数值解，即可得到结果。

5.3双联三叉杆式万向联轴器的动力仿真

5.3.1分析模型的建立
本分析模型是在第四章中的运动分析模型（图4-18）的基础上通过除去运动驱动，加上驱动力、摩擦力而得到图5-1所示的动力仿真模型。
目前在三叉杆式万向联轴器动力分析方面，所发表的论文大多是在忽略摩擦力与惯性力的条件下进行的，仅是作最基础的静力学分析，或是考虑到恒定摩擦和惯性力的动态静力学分析。而在实际应用中，摩擦不仅是联轴器实际失效的主要原因之一，而且是影响效率的主要因素，另外在联轴器高速运转中惯性力是不可忽略的重要因素。因此本章在考虑到摩擦和惯性力的情况下，进行真正的动力学分析（多刚体系统），必定会得出全新的结果，为这种联轴器的进一步研究、开发打下基础。

5.3.1.1建立模型的的关键点

5.3.1.1.1摩擦力的施加

在双联三叉杆式万向联轴器的模型中，相互运动的构件较多，各个构件之间的活动接触面都会产生摩擦力的作用，不同的运动副形式，摩擦产生的来源也不一样，在施加摩擦时要根据不同的摩擦来源考虑各因素的影响。在本章的分析中，各个运动副间都被加上了摩擦力。由于涉及到了如下四种运动副，现对它们摩擦力施加的考虑因素作如下的陈述：

移动副：

移动副产生摩擦的示意图如图5-2所示。在这种运动副中只会产生逆向于移动方向v（如图5-2中蓝色箭头所示）的摩擦力F_frict（如图5-2中红色箭头所示）,它的产生主要由三种因素，即构件间相互作用的径向力F、构件间相互作用的扭矩T_n、构件间相互作用的弯矩T_m（这三种力如图5-2中绿色箭头所示）。在施加由这些作用力产生的摩擦力时，要考虑径向力F的大小、等效作用臂长R_n（如图5-2中右边图所示运动副间的重叠量和重叠量的变化情况、扭矩T_n的大小和它的等效反作用臂长R_n、弯矩T_m的大小和弯矩的反作用臂长X_S（如图5-2中间图所示）。另外还得考虑静摩擦系数、动摩擦系数及预载荷的作用。

圆柱副：

圆柱副产生摩擦的示意图5-3所示。在这种动动副中会产生逆向于移动方V（如图5-3中蓝色箭头所示）的摩擦力F_frict（如图5-3中红色箭头所示）及逆向于旋转方向ω（如图5-3中蓝色箭头所示）的摩擦扭矩F_frict（如图5-3中红色箭头所示），它的产生主要由两种因素，即构件间相互作用的径向力F、构件间相互作用的弯矩T_m（这两种力如图5-3中绿色箭头所示）。在施加这些作用力产生的摩擦力时，要考虑径向力F的大小、圆柱半径R_P（如图5-3中间图所示）、运动副间的重叠量和重叠量的变化情况、弯矩T_m的大小和弯矩的反作用臂长X_s（如图5-2中右图所示），另外还得考虑静摩擦系数、动摩擦系数及预载荷的作用。

旋转副：

旋转副产生摩擦的示意图如图5-4所示。在这种运动副中只会产生逆向于旋转方向。（如图5-4中蓝色箭头所示）的摩擦扭矩T_frict（如图5-4中红色箭头所示），它的产生主要由三种因素，即构件间相互作用的径向力F_r、构件间相互作用的轴向力F_a、构件间相互作用的弯矩T_r（这三种力如图5-4中绿色箭头所示）。在施加由这些作用力产生的摩擦力时，要考虑径向力F_r的大小、圆柱半径R_P（如图5-4右图所示）、轴向力F_a的大小、摩擦半径R_n的大小（如图5-4右图所示）、弯矩T_m的大小和弯矩的反作用臂长（即旋转副的长度，如图5-4中左图所示），另外还得考虑静摩擦系、动摩擦系数及预载荷的作用。

球面副：

球面副产生摩擦的示意图如图5-5所示。在这种运动副中只会产生逆向于旋转方向的摩擦扭矩T_frc（如图5-5中红色箭头所示），它的产生只有一种因素，即构件间相互作用的径向力F（如图5-5中灰色箭头所示）。在施加由相互作用的径向力F产生的摩擦力时，要考虑径向力F的大小和球半径，另外还得考虑静摩擦系数、动摩擦索数及预载荷的作用。
在这一过程中分别对20个运动副添加了摩擦力，这些力在仿真中将会随着。它们的产生因素的变化而变化。这在后面的结果中可以见到。

5.3.1.1.2驱动力的施加
在动力仿真中，对微分方程的求解用的都是用数值计算的方法，在迭代求解的过程中，步长不可过长，如果步长太大，则在数值计算中会不收敛，导致仿真的失败。在动力仿真中，如果规定了时间步的步长，又添加了过大的驱动力，则在仿真中物体在较短的时间内会发生很大的空间位移，在这种情况下，数值计算将很可能不收敛．故在进行动力仿真中，应让整个变化过程平缓的进行，仿止出现上述的现象。
在ADAMS中提供了阶梯函数（STEP函数），它可以作为解决这一问题的工具。STEP函数简述如下：
在ADAMS中，STEP函数近似一个标准的数学STEP函数（没有不连续性）,并逐步逼近数值，例如：驱动或者力，向上或者向下或者打开和关闭。它的函数图形如图5-6所示。格式同各参数说明如下：

格式：STEP(x,x0,h0,xl,hl)
参数说明：
x一自变量，可以是时间或时间的任一函数；
x0一自变量的STEP函数开始值，可以是常数或函数表达式或设计变量；

x1一自变量的STEP函数结束值，可以是常数、函数表达式或设计变量；

h0一STEP函数的初始值，可以是常数、设计变量或其它函数表达式；

h1一STEP函数的最终值，可以是常数、设计变量或其它函数表达式；

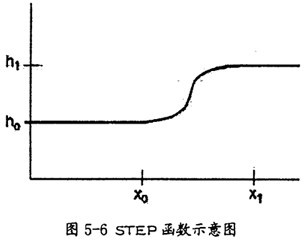
从以上说明中，可以知道，STEP函数能使数值之间的过度平缓。在本次仿真中正是利用了这一点，在施加驱动力时采用了此函数，让驱动力从O平缓过度到一个较大的值，使仿真平稳地进行，避免了发散现象。
在这一过程中分别在输入轴同支承间的旋转副及输出轴同支承间的旋转副上添加了STEP函数力矩驱动（输出轴同支承间的旋转副上的驱动作为负载，输入轴同支承间的旋转副上的驱动作为主动力矩）。

5.3.1.2模型的检验
建立好模型后，对模型进行检验，结果如下：
模型中共有15个构件；
有6个圆柱副，2个旋转副，6个球面副，6个移动副；
模型共有8个自由度（Gruebler数），且每个约束均为必要，无冗余；（此过程显示非常重要，如果检验中有冗余的约束，则在求解的过程中，ADAMS会除去这些约束，但除去这些约束在那个运动副上是不可控制的，那样的后果是在动力仿真中中得到的运动副上的反作用力就不正确，只能通过在柔性体的动力仿真中才可加以补救。此模型中约束正好无冗余，这样在每个运动副中所测量的反力都应是正确的。)

在模型的两端加有两个力矩，-个用作主动力矩另-个则用作被动力矩；

在每个运动副中均有摩擦，共施加20个摩擦力。

5.3.2动力仿真
通过设定-定的仿真步数，选用-种适合于刚性系统（特征值变化大的系统），且积分稳定性好的求解器（本次仿真选用了MODIFIED求解器。因为在ADAMS提供的GEAR,DASSL,MODIFIED,ABAM,SI2这五种求解器中，GEAR、DASSL、MODIFIED求解器适合于刚性系统，且积分稳定性的关系为：MODIFIED>DASSL>GEAR。），进行动力仿真，并输出如下测量结果：

STEP函数的变化曲线（如图5-7所示）；
输入轴转角的变化曲线（如图5-7所示）；
输入轴角速度的变化曲线（如图5-7所示）；
小杆受力曲线（如图5-8所示）；
轴颈受力曲线（如图5-9所示）:
小杆受摩擦力曲线（如图5-10所示）；
轴颈受摩擦力曲线（如图5-11所示）；
输入轴、输出轴由附加弯矩产生的摩擦扭矩（如图5-12所示）。

以上所有的测量结果均是在同-次仿真中得到，仿真历时0.8秒，双联三叉杆式万向联轴器在仿真中经历了从启动到平稳波动的动态过程。在所有力的测量曲线中，曲线有突变现象，这-现象可能同模型中的刚体假设，以及静摩擦系数到动摩擦系数和突变有关，如果用柔性体代替刚体，其结果应该会平滑。但总的来说，这里的曲线在-定的程度上反应了这些力的变化趋势，也可以作为分析的参考。

5.4仿真结果分析

由图5-7可以看出，双联三叉杆万向联轴器在动力仿真的过程中，输入力矩逐步以STEP函数的趋势增大，当其克服静摩擦力后，开始转动，在角速度达到一定的值后，出现波动的现象（红色线条所示），并非如平常想象的近似等速转动。

由图5-8可以看出，双联三叉杆式万向联轴器在动力仿真的过程中，一端的三个小杆在移动副中受到力逐步增加，当系统开始转动后，它们受到的力呈现有规律的波动，但互相之间有一个相位差。正是由于它们的受力变动复杂，故它们在滑杆套轴上的三个反力的向量和就可能不为0，这样的结果是，它们除此之外在滑杆套轴（输入轴）上形成负载扭矩外，还会产生附加弯矩的作用。

由图5-9可以看出，双联三叉杆式万向联轴器在动力仿真的过程中， 双联三叉杆一端的三轴颈同内球头的圆柱副上的作用力变化趋势同图5-8中的小杆变化趋势是相同的。由于它们的受力变动复杂，故这三力在双联三叉杆一端上的向量和也可能不为0。这样在双联三叉杆上也会产生附加弯矩的作用。而且轴颈受力平均较小杆的受力要大。

由图5-10可以看出，双联三叉杆式万向联轴器在动力仿真的过程中，其一端的三小杆同滑杆套轴间的摩擦力变化相当有规律。当小杆相对滑杆套轴运动反向时，它们就会在正负间有规律的切换。

由图5-11可以看出，双取三叉杆式万向联轴器在动力仿真的过程中，其一端的三内球头同轴颈间的摩擦力变化相当有规律。当内球头相对轴颈运动反向时，综们就会在正负间有规律的切换。但在这里产生摩擦力的平均大小要较小杆上的小得多。

由图5-12可以看出，双联三叉杆式万向联轴器在动力仿真的过程中，其一端的三个小杆所受的摩擦力的合力变动较有规律，其值在开始一段平滑，其后几乎以0为中心波动。由于这三个摩擦力的方向均平行于输入轴或输出轴轴线，故此合力会在输入轴和轴出轴上产生轴向的力，在输入轴和输出轴上产生摩擦扭矩。如取其水平较高值60牛来计算，它产生的摩擦扭矩为270N·mm（60×0.3×15=270，其中0.3为动摩擦系数，15为摩擦半径），此值相对图5-13中的值而方相当小。

由图5-13可以看出，双联三叉杆式万向联轴器在动力仿真的过程中，输入轴和输出轴上的摩擦扭矩逐渐增加，然后开始一种复杂的波动。由于本次仿真是在无重力的环境下进行的，因此，不会因为重力的作用在输入轴和输出轴上产生弯矩和由其产生的反作用力而形成弯矩，当然也就没有它的作用而形成的摩擦扭矩，则只有可能是三小杆同滑杆套轴间的作用力而导致在滑杆套轴上产生的轴向力和弯矩而产生此摩擦扭矩，但由图5-12的分析可知，轴向力产生的摩擦扭矩很小, 则可以证明滑杆套上有较大的附加弯矩存在，而且它是形成摩擦扭矩的主要原因。

5.5本章小结

本章中阐述了机械动力学的几种分析方法，明确了动力分析方法的趋势。并在多刚体动力学的理论基础上，利用目前最为流行的多体动力学软件ADAMS,对双联三叉杆万向联轴器进行了动力学模型的建立和动力仿真，得到了许多可视化的结果。证明这种联轴器在传动中其受力相当的复杂，并得出了一些定性的结论，这种联轴器的进一步研究开发打下了基础。