三叉杆式万向联轴器的振动分析

6.1引言
万向联轴器是一种典型的回转机械，而对回转机械的转子无论静平衡做得如何好，仍会有不平衡惯性力存在，激发机械系统产生振动。三叉杆滑移式万向联轴器输入轴以恒定角速度转动时，由前面分析可知输出轴的转速和承受的扭矩均作微小的周期性变化，同时在输入轴上还有周期变化的弯矩，因此系统在这种周期性的激励下振动的产生是必然的。而对于联轴器这种结构系统来说，不希望有过大的振动发生，因为振动会造成结构的共振和结构疲劳而使结构破坏；还可能在系统中往往产生很大的扭转附加载荷，不仅使系统中零部件发生断裂，同时还会使系统向外界发出噪声，严重影响系统的可靠性和耐久性。同时还将引起其它系统的振动和噪声，从而影响整个系统的性能。
故而，正确、有效地确定共振频率，尽可能避开共振区运行（很多情况不一定能避开，那就需要改进设计），对设备的设计、安装、使用、维护有重要意义。

6.2振动分析采用的一般方法
对于结构系统的振动分析，目前的计算方法主要有经验公式法，传递矩阵法，有限元法等多种方法。
经验公式法―经验公式法是对某些成型的结构列出其经验公式，通过这种公式对结构的固有频率进行计算。这种方法适用范围非常有限。

传递矩阵法―传递矩阵法是将一个连续系统离散化为一系列相互连接的子系统，根据所要研究的问题，选取一系列的状态向量，各个相互连接的子系统之间的关系可以通过由这些状态向量组成的传递矩阵表示，这样从起点推算到终点，再根据边界条件得到系统的频率方程，即可得到系统的固有频率和模态向量。
有限元法一一有限元法是一种数值计算方法。它的基本思想是将问题的求解域划分为一系列的单元，采用单元体对连续弹性体进行简化，但质量和弹性是分布的，不是集中的，单元之间仅靠节点相连。单元内部的待求量可由单元节点间通过选定的函数关系插值得到。由于单元形状简单，易于用平衡关系和能量关系建立节点间的方程式，然后将各单元方程集组成总体代数方程组，计入边界条件后可对方程求解，得到物体的运动特性。现阶段由于CAD、CAE软件的日益成熟，以及电脑硬件性能的大大改善，这种方法已成为一种流行的分析方法。

6.3本章分析采用的方法
本章分析采用的是基于虚拟样机技术进行的传动系统振动分析，其实质是有吧元方法，即通过对各构件的模态进行模态叠加和模态综合而得到系统的固有频率和振型。

其简要的步骤是如下：

首先通过CAD软件（Pro／E）建立双联三叉杆式万向联轴器的零件模型和装配模型；

接着运用有限元分析软件ANSYS建立了各零件的有限元模型，获取模态并生成柔性体描述文件一一模态中性文件（MNF文件）；
然后在ADAMS中建立双联三叉杆万向联轴器的刚性体模型，再利用上一步生成的MNF文件，生成系统各构件的柔性体，将柔性体取代相应的刚体，得到系统的柔性体模型；
最后在ADAMS中，利用ADAMS的振动分析模块ADAMS/Vibration完成整个系统的振动特性的分析。

6.4振动分析的理论背景

6.4.1有限元软件ANSYS简介
一般机械系统的几何结构相当复杂，受的负载也相当多，理论分析往往无法进行。想要解答，必须先简化结构，采用数值模拟方法分析。由于计算机行业的发展，相应的工程分析软件也应运而生，有限元软件ANSYS就是其中之一目前ANSYS软件在工程上应用相当广泛，如机械、电机、土木、电子及航空等领域都有大量的使用。而且它能达到某种程度的可信度，颇获各界好评。使用该软件，能够降低设计成本，缩短设计时间。
以ANSYS为代表的工程数值模拟软件，是一个多用途的有限元法分析软件，可用来求解结构、流体、电力、电磁场及碰撞等问题。它包含了前置处理、解题程序以及后置处理。将有限元分析、计算机图形学和优化技术相结合，已成为现代工程学问题必不可少的有力工具。

6.4.2MNF文件

模态中性文件一一MNF文件，是柔性体描述文件，该文件中包含了柔性体的几何信息（包括节点的位置及其连接）、节点的质量同转动惯量、各阶模态、模态的广义质量和广义刚度等信息。在有限元软件胡SYS中就可以生成此文件。利用此文件可以在多体动力学软件ADAMS中生成刚体的柔性体模型。此文件仅适用于线性结构受力行为。

6.4.3模态叠加
模态叠加法是建立在模态的正交性及展开定理的基础上的一种求解动力响应的近似方法。ADAMS之所以能够根据不同的外力状态适时反应出正确的变形结果，正是利用了“模态叠加（Modal解Superposition）理论”，由有限元分析（FEA)计算出特征值、特征向量、和模态，再由模态叠加关系式，即可计算得到各点的变形量。其具体理论如下：
一个具有N个自由度的系统的强迫振动方程为：
[M]{ }+[C]{ }+[K]{x}={f}
{x}——位移向量                         [M]——质量矩阵
{ }——速度向量                         [c]——阻尼矩阵
{ }——加速度向量                       [K]——刚度矩阵
{f}——激励力向量
对于一般的已知激励力，运用数值计算方法总是可以解出响应来的。然而，对于大型结构，具有非常多的自由度，响应的计算耗费是巨大的。一般的计算过程是这样的：
求该系统的特征值与特征向量
由该式的特征方程：det（-W²[M]-[K]）=0

求得N个特征值及相应的特征向量

 

于是q_r可以单独求解。

在求得所有的q_r后，即求得{q}后，可按下式来计算结构系统各点的响应

{x}=

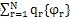
上述过程称为模态叠加法， q_r可以理解为第r阶固有振动模态对实际振动{x}所作的贡献。各阶模态所作贡献的大小除取决于结构本身的特点外，还取决于结构受激励力的频率范围，以及激励力分布的情况。理论上，对于一个N自由度的系统，可以通过方程解耦确定模态坐标响应，然后通过线性变换得到物理坐标响应。但实际上在一个系统的振动中仅是较少几个模态在起主导作用，因此只考虑这些模态的作用，而无需求解全部的方程，这样做虽然是近似的但却有足够满意的精度，这便是模态叠加法的出发点。

6.4.4模态综合
由于对我们起指导作用的是一个系统的动特性，即系统的固有频率和振型，因此，在求得单个构件的固有频率和振型后，我们应进行模态综合，即部件的模态分析或称动特性分析。
在模态综合中应请注意如下几点：
在求得自由系统的模态后，若要再考虑边界条件的影响，是可以通过计算来完成的。反之，在某种非自由边界条件下取得的结果，很难被转化到其它的边界条件的情况。故单个构件的模态应是自由边界下得到的。
特别应该指出的是，自由系统的模态中，不应忽略刚体模态。仅有部件弹性模态不能用于整体结构的综合。
部件是整体结构的一部分。部件的模态向量应保证其在与整体连接的那些点有值。否则不能进行整体模态综合。
部件的分析模态的阶数一般少于部件的自由度。但一定要大于部件在整体连接时的连接点自由度数。

6.4.4.1模态综合理论：
这里所述的仅是模态综合理论中的一种方法，在这种方法中，采用各部件的自由模态（或非约束模态）来进行综合，但综合后的整体结构模态数，将由各部件所包含的模态数来确定。

设有总值年I和部件Ⅱ，通过弹簧和阻尼构件相连接，如图6-1所示。对于部件I，应用

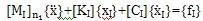
                                （6-1）

式中{f₁}仅为作用于连接点上的内力。假定我们已对部件I作了模态分析，因此上式可转化为用模态坐标表达的形式

将（6-6）式代入（6-5）式，得

由于[K_C]和[C_C]不是对角阵，因此上式是一组耦合方程。上式缩写为

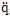
[I]{ }+[K_CO]{q}+[C_CO]{ }={O}

对于小阻尼系统，可按常规方法，先用

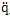
[I]{ }+[K_CO]{q}={O}

求组合系统的特征值及特征向量，然后可建立组合系统的模态模型。（不难看出，此处组合结构整体的特征值的数目由各部件的模态数来确定，而不是由它们的结构几何坐标数确定的）

6.4.5系统模态的有限元方法

通过对系统中的各构件进行有限元自由模态分析，得到各构件的自由模态（当然也包含了6个刚体模态），以各构件的连接关系为依据，建立边界条件，然后进行模态综合，即可计算得到整个系统的动特性和响应。其过程如图6-2。

6.5双联三叉杆式万向联轴器的振动分析

6.5.1振动分析过程

6.5.1.1柔性体模型的建立
建立柔性体模型是三叉杆式万向联轴器振动分析的基础，也是最繁琐的一步，其具体过程如下：
在CAD绘图软件Pro/E中建立各构件的三维外形图和整个系统的装配图；

将各构件的三维外形图分别导入有限元分析软件ANSYS，设定好分析类型、单元类型、实常数、材料属性、划分网格、建立耦合方程（刚性区域处理，实际上是各构件连接的边界条件）；
值得说明的是在这一步中关键点如下：
a.单元类型的选择
由于在刚性区域处理中涉及到点质量单元，在实体网格划分中涉及到实体单元，故在选取单元中包含如下两种单元：
①SOLID45 3-D STRUCTURAL SOLID单元

此单元为3-D固体结构单元，由八个节点组成，在单元的每一节点上有三个自由度，即分别沿着三个坐标轴的方向。此单元可以进行塑性、蠕变、应力硬化、大变形以及大应变分析，是结构分析中的最常用单元。单元结构如图6-3，此单元有两种退化形式（见图6-3右边）。

②MASS21单元

此单元为一个有六自由度的质量单元。此单元的第一个不同的坐标方向上可以施加不同的质量大小和转动惯量。质量单元是由单个节点、单元坐标方向的集中质量系数、单元坐标轴的旋转惯性所决定的。为了在加入质量单元后不影响系统的惯性属性，在此单元的实常数设定中惯性量应设定的非常小（如小于10^-4）。单元如图6-4所示。

b3刚性区域的处理

刚性区域的处理是基于小变形理论，通过这种处理，单个构件的自由模态频率会上升，只有通过这种处理可以在ADAMS中进行模态叠加和模态综合，得出系统的固有频率。其处理的方法是根据构件间的不同的运动副连接形式，用点质量单元上的节点（有时物体上自己的节点也可，不一定非要再建立质量单元）和实体上相应的节点进行耦合，形成主节点和从节点关系，构成刚性区域。其连接形式如图6-5，在此图的连接形式中，a图的连接形式可以传递所有载荷形式，是一种推荐的连接方式；c图中主节点仅同单个从节点相连传递的载荷形式有限，不合适选用。

定制好单位系统，选择好同外部连接点，执行ANSYS中的ADAMS宏命令（在命令中输入提取前20阶模态），进行MNF文件的生成。双联三叉杆万向联轴器的关键构件在ANSYS中的模态分析模型分别如图6-6、图6-7、图6-8（红色区域为刚性区域）:

将系统在CAD软件Pro/E中的三维刚体装配模型通过Pro/E同ADAMS的接口程序MECHANISM/Pro导入到多体动力学软件ADAMS中，加上各构件间的运动副，形成系统的ADAMS刚性体模型；
在ADAMS中利用其模块ADAMS/FLEX将生成的MNF文件调入刚性体系统模型，生成各构件的柔性体模型，并用ADAMS/Linear模块对柔性体进行检验，看是否同ANSYS中计算得到的固有频率是相近的，否则计算是不对的。然后修改各个柔性体的模态成分，其首要任务是关闭掉各柔性体的刚体模态（由于ADAMS/Flex会给每个柔性体赋予六个非线性的刚体自由度，如果柔性体还包含刚体模态，求解时就会产生奇异）；其次是为了提高仿真效率，对运动没有贡献的模态不予采用。在修改各个柔性体构件模态成分的同时，我们可以选出它们参与振动分析的固有频率，分别如表6-l、表6-2、表6-3所示；
用修改后的柔性体替换相对应的刚体模型，保留各构件间的运动副不变，删除被替换后的刚体。这样就形成了系统的柔性体模型，如图6-9所示。

表6-1 双联三叉杆的部分固有频率

表6-3 滑杆套轴的部分固有频率

 

6.5.1.2系统固有频率的求解

在双联三叉杆式万向联轴器的柔性体系统模型建立后，再对各构件间的运动副进行修补（由于在刚体同柔性体的替换过程中有的运动副可能会遭到破坏），这样可以得到系统的振动分析模型，如图6-10所示。这时才可以对其进行整个系统的动特性求解。利用ADAS的振动模块ADAMS/Vibration，设定其求解类型为一般模态求解，即可得到此系统的部分固有频率，其结果见表6-4。同时作者提取了系统的第60阶、第76阶和第100阶振型（这几阶振型只是作为振动中变形的一个示意），分别如图6-11、图6-12和图6-13所示。

6.5.2结果分析

从表6-1、表6-2、表6-3同表6-4的频率值的比较以及分析过程中所看到的各构件和双联三叉杆万向联轴器系统的振型，发现了如下现象：

尽管系统中各构件的固有振动频率值比较高（经刚体区域处理后），但是当它们组成一个双联三叉杆式万向联轴器系统后，得到的系统的固有振动频率会显著降低；

尽管系统各构件的振型比较简单，但是当它们组成三叉杆式万向联轴器系统后，系统的振型会变得相当复杂。

表6-4 双联三叉杆式万向联轴器的部分固有频率

6.6本章小结
本章综合运用有限元软件ANSYS、多体动力学软件ADAMS中的ADADS/F1ex、ADAMS／Linear和ADAMS/Vibration模块对双联三叉杆万向联轴器系统进行了振动分析，得到了此系统各构件的部分固有频率和振型以及系统的部分固有频率和振型。为以后动力特性中的响应分析打好了基础。
在本章的分析中，由于各构件的刚性区域处理中考虑到从节点的个数太多会大大增加耦合方程的数量，使计算效率显著降低，故而在选取从节点时相应减少了它的数量，在一定的程度上可能会影响计算的准确性，但是本章主要是侧重在系统的动特性求解中探讨一种可行的分析方法。
本章所采用的计算方法彻底地改变了以往用传递矩阵法，通过简化模型，线性化处理，人工建立微分方程的历史，大大提高了计算的效率和精度。它的最大的优点就在于系统的精确性和可装配性、分析过程的方便快捷、分析结果的直观性。而且还可以综合考虑非线性特性的影响，求得更加真实的解。因此，基于虚拟样机技术进行动力传动系统振动分析具有一定的新颖性和实用性。
一般来说只有在弱阻尼的条件下的位移共振频率和加速度共振频率接近于系统的固有频率。故本章中所求得的固有频率并非是结构的共振频率，而且即使外力的频率同共振频率一致，也不一定会发生共振。要想获得真实的响应特性必须进行响应分析。