推杆减速器的结构分析与齿形综合

本章根据推杆减速器的结构特征，找出了推杆内外滚子工作角之间的关系。这种关系不仅适用于激波器廓形为偏心圆的单激波推杆减速器结构，而且也适用于激波器廓形为非圆弧曲线的多激波推杆减速器。利用内外滚子工作角之间的关粤和法向等距线的几何性质，首次分析研究了激波器廓形为任意形状非圆弧曲线的多激波推杆减速器的齿廓形成理论，与传统的包络法相比，具有概念清晰，所得公式形式简单的特点，通过实例计算，证明了激波器为偏心圆的推杆减速器，其内齿圈齿廓曲线不是摆线这一重要结论。

2.1推杆减速器的结构及传动比计算

推杆减速器的结构简图如图2.1所示，它由四个部分组成：

1.激波器J    由输入轴1、偏心套2、转臂轴承3所组成。为平衡激波器所产生的惯性力和抵消激波器上的径向力，一般采用双排结构，并使它们的相位差为180°。

2.传动圈C    传动圈是一个具有双排等分槽的构件，它与输出轴固联。

3.装有内外滚子的推杆   内外滚子一般是短圆柱滚子。

4.内齿圈N   内齿圈的齿形是与运动的推杆外滚子相共轭的曲线。与激波器对应，采用两个完全相同的内齿圈互成180°布置。
推杆减速器的工作原理为：当驱动力矩由输入轴输入后，它以等角速度、转动，带动偏心圆激波器绕固定中心。转动，由于偏心圆激波器径向尺寸的变化，激波器产生径向推力，推动着推杆在传动圈的径向导槽内向外移动。推杆的径向运动受到固定于机座上的刚性内齿圈的约束，作用于推杆外滚子上的约束反力迫使推杆驱动具有导槽的传动圈以等角速度ω_C转动，于是实现了定速比的速度变换及功率的传递。
在推杆减速器中，设激波器按顺时针方向旋转，则传动圈C，内齿圈N的转向可能与激波器相同，也可能相反（图2.2）。为了研究问题的方便，本文中称传动圈与主动件激波器转向相同的结构为正向结构（图2.2（a）)，称传动圈与激波器转向相反的结构为反向结构（图2.2(b))。

推杆减速器的正反向结构形式完全取决于内齿圈N的齿数Z_N、理论推杆数Z_C以及激波器J的激波数Z_J。

对单激波来说，当理论推杆数Z_C比内齿圈齿数Z_N多1（即Z_C­=Z_N+l）时，推杆减速器为正向结构（如图2.1(b）所示）。而当推杆数Z_C比内齿圈齿数Z_N少l（即Z_C=Z_N-1）时，推杆减速器是反向结构（如图1.5所示）。当推杆数Z_C等于内齿圈齿数Z_N时，机构不能工作，而当推杆数Z_C与内齿圈齿数Z_N之差在1以上（即Z_C>Z_N+1或Z_C<Z_N-1）时，机械也不能工作。

类似分析可得出结论：对于多激波推杆减速器，要使机构能够工作，齿数关系必须满足：

                          Z_C=Z_N±Z_J                                     （2.1）

并且Z_N应是Z_J的整数倍。当式（2.1）取“+ ”号时，推杆减速器为正向结构，取“一”号时为反向结构。

固定激波器J、传动圈C、内齿圈N这三个构件中的任何一个，而其余两个构件的角速度之比称为这两个运动构件的传动比。传动比用i表示，并用下标表明相应两个运动构件及其主从关系。如i_CN表示激波器J固定时，传动圈C的角度速度与内齿圈N的角速度之比值。当这两个角度速成方向一致时，传动比取正值，反之传动比取负值。

利用行星齿轮传动中确定传动比的相对角速度法，很容易得到各种运动形式的传动比，如表2.1表示。

上面所说的推杆数Z_C是理论上的推杆数，在工程实际中，当推杆减速器要实现的的传动比较大时，在传动圈的圆周上不能够开出理论推杆数Z_C那么多的导槽，常采用“抽杆”技术，即每隔一定的间隙，抽掉一个或几个推杆，抽杆后当然不能影响整个传动机构的连续运转及传动比。

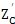
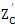
抽杆后，机构的实际推杆数 要小于理论推杆数Z_C。为了保证抽杆后受力均衡，要求抽杆是均匀的，抽杆前后推杆都是均布的。设n为每隔一个推杆所抽掉的推杆数，则实际推杆数 与理论推杆数Z_C的关系应为：

从推杆减速器的结构及工作原理可以看出，由于激波器采用了滚动轴承，使得与内滚子相啮合接触的激波器外环在工作过程中只是摆荡，从而减小了与内滚子相啮合时的滑动摩擦。另外，只要能使外滚子转动灵活，内齿圈齿廓与外滚子之何的滑动摩擦也可变得很小。可见，推杆减速器中滑动摩擦以推杆与导槽之间最为严重。
工程技术人员在实践中围绕着传动圈的结构提出了不少改进方案。一种想法是在推植与导槽之间加放滚针，轨图2.3所示，使移动副转换成通过滚动体接触的滚动副。但由于实际生产中工艺上的原因，这种方法没有被采用。

图2.4所示是推杆与导槽所构成的移动副的另外几种形式，它们也未能很好地解决移动副所带来的滑动摩擦问题。

当把推杆去掉，内外滚子合而为一时，便是滚柱活齿减速器的结构。还可以将激波器设计成内工作轮廓，内齿圈设计成外齿轮（波形轮），这种结构称为外波式活齿传动结构。

2.2内齿圈齿廓的法向等距线及性质

取固定坐标系（o，x，y）及分别与激波器和内齿圈固联的坐标系（o，x_J，y_J，）和（o，x_N，y_N），如图2.5所示，它们在初始位置是重合的。
设以y_J为坐标极轴，激波器J的廓形H_J的表达式为T_J=T_J（θ），则内滚子中心0₁的轨迹H₁是这样形成的：设H_J上任意一点M₁处的单位法线向量为 ，在法线上，取长度T_z（T_z等于滚子半径），得一点O₁，则这个点就在H₁上，这样逐点形成的H₁ 与H_J是法向等距线，它们在对应点有共同的法线。证明如下：

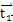
这表明，H₁在0₁点处的切线向量 与 垂直，即 既是H_J在M₁点的法线，又是H₁在0₁点的法线，得正。

下面再推导一下齿廓及其法向等距线的相对曲率关系。设H_J的孤长参数为S_J，相对曲率为k_J，而H₁的孤长参数为S₁，相对曲率为k₁，由微分几何可得：

最后得到法向等距线在对应点的相对曲率关系为：

                      k_J=k₁/（1-T_zk₁）                                （2.3）

相对曲率半径关系：

                         P_J=P₁-T_z                                    （2.4）

内齿圈的齿廓H_N与外滚子中心的轨迹H₂也是法向等距线，它们在对应点也有共同的法线，相对曲率与相对曲率半径也有和上面类似的关系。

2.3内外滚子工作角之间的关系

设在某一时刻，激波器与内滚子相切接触在M₁点，内齿圈齿廓与外滚子相切接触在M₂点，如图2.5所示，则图中a₁与a₂分别叫做内外滚子工作角。在工作行程，a_l及a₂都为正值，在非工作行程，它们都为负值。

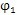
上面已说过，内滚子中心的轨迹H₁是激波器廓形H_J的外法向等距线，激波器按顺时针方向转动时，H₁是一条以转角 为参数按逆时针方向生成的有向曲线，设其方程式为：

ι₁=ι₁（ ）

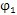
由微分几何知，曲线H_l的向径与切线正方向的夹角μ₁可由下式计算：

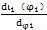
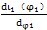
切线的正方向应取与曲线极角的计量方向一致，当 大于零时，μ₁在0至π/2范围内取值，当 小于零时，μ₁在π/2至范围内取值。

由（2.5）式可得：

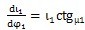
                                                              （2.6）

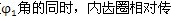
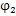
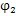
如图2.5所示，设激波器相对传动圈顺时针转过 动圈反方向转过了 角（对于反向结构，内齿圈则相对传动圈按与激波器转向相同的方向转过 角，见图2.6）。

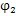
外滚子中心0₂的轨迹H₂是内齿圈齿廓的内法向等距线，它可以看作是一条以 为参数按顺时针方向形成的有向曲线（对图2.6所示反向结构，H₂是一条按逆时针方向形成的有向曲线H₂的方程为：

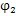
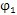
                         ι₂=ι₂（ ）=ι₁（ ）+ι                      （2.7）

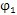
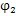
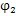
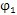
将 与 分别作为上述有向曲线H₁及H₂的参数，无论对于正反向哪种结构, 随着 的增加而增加，并有关系式

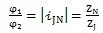
                                                           （2.8）

同样，由微分几何，曲线H₂的向径与切线正方向的夹角μ₂可由下式计算：

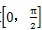
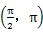
分析图2.5及图2.6可知，当μ₁及μ₂的取值在 范围内时，a₁及a₂为正值，当μ₁及μ₂的取值在 范围内时，a₁及a₂为负值，故恒有下面的式子成立：

2.4.1内齿圈的齿廓方程
为了提高加工精度及降低成本，推杆内外滚子通常选用半径相等的短圆柱滚子标准件，这样，对激波器廓形和内齿圈齿廓两条曲线只要知道其中之一，便可根据机构传动比、推杆长度及滚子半径来确定另外一条曲线。
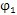
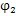
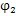
设选定激波器廓形为T_J=T_J（θ），按通常的极坐标表示法，θ增加的方向为逆时针方向。由激波器廓形方程便确定了激波次数Z_J。设激波器相对传动圈从初始位置顺时针转过了 角，对正向结构，内齿圈相应地相对传动圈逆时针转过了 角（图2.5)，对于反向结构，内齿圈相应地相对传动圈顺时针转过了 角（图2.6),由图可得：

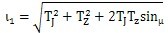
                                          （2.17）

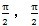
上式中的μ为曲线H_J在M₁点的向径与切线正方向的夹角。前面已说过，曲线向径与切线正向的夹角μ的取值范围是［O，π]。在用计算机解算时，反正切函数arctg（x）的值域是（- ），所以为了使概念明确和使用方便，特定义下面在本文中使用的函数：

上式中T_J（θ）表示极径，其值当然为正。

这样（2.17）式中的μ可表示为：

由图2.5（或图2.6）中的△OM₁O₁还可得

按关系式（2.16）可计算出外滚子工作角a₂

而

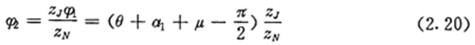
对于图2.5所示正向结构，在与内齿圈固联的坐标系中，得到外滚子中心轨迹H₂的方程为：

对于图2.6所示的反向结构，在坐标系（0，x _N，y _N）中，得到内齿圈齿廓的方程为：

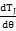
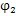
每给定一个θ值，由激波器廓形方程式计算出T_J, 接着计算 及μ，然后把由(2.17）式算出的ι₁的值和由（2.19）式算出的a₁的值代入（2.16）式，可算出相应的a₂，由式（2.20）便可得到 ，最后把这些值代入（2.21）式（反向结构代入（2.22)式），便可得到内齿圈齿廓上相应的一个点M₂的坐标值（x_N，y_N）。当θ在激波器的一个周期内取一系列点时，相应的M₂点描绘出内齿圈齿廓上一段工作齿廓与非工作齿廓曲线的图形。

由上面可以看出，在选定激波器廓形T_J=T_J（θ）的情况下，正反两种结构所得到的内齿圈齿廓方程式（2.21）与式（2.22）在形式上是不同的。对于反向结构，用-θ代换激波器方程中的θ，即令T_J=T_J（-θ），则θ增加的方向为顺时针方向，若激波器廓形可表示为偶函数，即T_J（一θ)=T_J（θ），让激波器按逆时针方向转动，则所得的内齿圈齿廓方程式完全与（2.21）式相同。因而齿廓方程式（2.22）与式（2.21）虽然形式不同，但实质是一样的。区别在于参数吸的取值方向，今后以式（2.21）作为内齿圈齿廓的标准形式。

2.4.2内齿圈齿廓的曲率及曲率干涉的校核
内齿圈齿廓曲线上某点的曲率，表示该点附近齿廓曲线的弯曲程度，反映了齿廓曲线的几何特性，是研究机构性能的重要参数。前面说过，内齿圈的齿廓H_N与外滚子中心轨迹H₂是法向等距线，它们在相应点的曲率有一定的关系，所以要求H_N的曲率，可以先求出外滚子中心轨迹H₂的曲率。
根据微分几何，外滚子中心轨迹H₂的相对曲率k₂可由下式计算：

由（2.5）式可得：

这样，由（2.24）式便可得到在外滚子中心轨迹上与激波器任一角度θ对应点的相对曲率k₂，而内齿圈齿廓H_N上对应点的曲率k_N为

在对应于内齿圈的齿顶部分，当曲线H₂的最小曲率半径P_min小于或等于滚子半径时，即P_min≤T_Z时，则内齿圈齿廓曲线H_N在齿顶处发生交叉，结果使齿顶变尖，称这种现象为顶切。顶切将使机构的传动特性受到影响，使同时参加工作的推杆数目降低。由（2.24）式可计算出曲线H₂在对应于齿顶处的相对曲率k_2a，不发生顶切的条件为：

另外，当选用半径为T_d的刀具加工内齿圈齿廓时，在齿根处可能发生切削干涉（过渡切削）。同样由式（2.24）可计算出曲线H₂在对应于齿根处的相对曲率kZ 了，齿廓曲线H_N在齿根处的相对曲率k_Nf为：

2.4.3 激波器为偏心圆的机构目前见到的推杆减速器，其激波器廓形都为偏心圆。设激波器廓形的半径为T_b，偏心距为e，由于接触点的法线0₁M₁必然通过偏心圆的几何中心，如图2.7所示，所以不需要列出激波器廓形的方程，而直接从几何关系就能计算出滚子工作角。

将它们代入（2.19）式，便得到（2.37）式。可见前面所得到的多激波计算公式对激波器为偏心圆的单激波也同样适用。在单激波情况下，内外滚子工作角之间的关系简化成了：

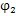
式（2.36）、（2.37）、（2.38）是偏心圆激波器的推杆减速器中ι₁、a₂与 的基本关系式，后面常用到它们。

代入（2.24）式及（2.21）式就可求得H₂的曲率及内齿圈齿廓H_N的方程。

当ι=0 时，内外滚子合而为一，这时的推杆活齿传动机构成了滚柱活齿传动机构，所以上面的各公式对滚柱活齿传动机构也适用，只需将其中的ι=O即可。

2.5由内齿圈齿廓反求激波器廓形

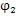
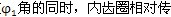
设选定内齿圈齿廓H_N的方程为T_N=T_N（θ），θ 增加的方向为逆时针方向，当内齿圈N相对传动圈转过角度 时，对应于激波器相对传动圈转过的角度为 ，如图2.8所示。设此时H_N与外滚子在M₂点接触，同样由微分几何，内齿圈齿廓曲

2.6 应用举例

设选定推杆减速器内齿圈齿廓为一外摆线，其方程为：

取e=5mm，z₁=11，R=120mm，用外摆法形成此曲线时，R表示基圆与发生圆半径之和，e表示定点离发生圆圆心的距离。取推杆长度ι=36mm，滚子半径T_z=10mm，求单激波时的激波器廓形。

由z₁=11知内齿圈为11个齿，即z_N=11。将摆线化成极坐标方程就是

上式中：

 

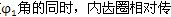
每给一个t值，按上述式子可算出相应的T_N及θ，经（2.40）式可算出μ, 然后由式（2. 41）、（2. 42 ）、（2.43）和（2.45）算出相应的ι₂、a₂、a_l及 。最后由式（2.47）可算出激波器廓形H_J上对应点的坐标值。一些点的计算数据如表2.2所示，由计算机绘出的激波器廓形如图2.9所示，它并不是一个标准的圆，图中圆的上部稍微有点凸出。由解的唯一性可推知，激波器为偏心圆的推杆减速器，其内齿圈廓形一定不是摆线，虽然形状相似，其实二者是不同的，这已为工程实际所证实。

表2.2  激波器廓形的计算值