内齿圈齿廓的加工及测量

4.1内齿圈齿廓的范成加工
目前，在推杆减速器的批量生产中，其内齿圈齿廓的加工采用的都是范成加工方法，加工的夹具及刀具的相对运动完全模拟减速器的运动。激波器的偏心距e由一个偏心轴的偏心距e来实现，激波器的半径T_b与内滚子半径T_z之和由偏心轴的几何中心至固定点的距离R来实现，传动比由挂轮的传动比来实现，如图4.1所示。

范成加工法具有快速、简易、经济的优点，其加式装置可作为附件加装在现有的滚齿机上。缺点是刀具必须完全与推杆外滚子直径相同，而且对于推杆减速器的每一和中不同规格都要更换工装，不利于产品系列化生产。尽管加工装置本身可以调整得很精确，但常因刀具的磨损、进刀深度掌握不当，以及刀具轴线沿内齿圈径向出现偏距等问题给被加工的齿圈带来很大误差。

4.2内齿圈齿廓的数控加工

内齿圈齿廓可用数控铣进行粗加工，用数控磨进行精加工。本节主要讨论在Y₅₄非圆搂控插齿机上的加工方法。

4.2.1Y₅₄数控插齿机加工齿廓曲线的原理

经Y₅₄插齿机改造成的非圆数控加工机床，由X、C、D三轴联动来实现对给定曲线的数控加工，如图4.2所示，D轴是刀具的回转中心轴，加工齿廓曲线时，采用圆形插刀，插刀一边绕D轴旋转，一边沿D轴作上下往复运动。C 轴是工作台回转轴，被加工的工件加在工作台上。沿X 轴的移动保证了沿齿深方向的进刀量。X轴始终在刀具回转中心D轴及工作台回转中心C轴的连线上。这三个轴分别由被脉冲信号驱动的三个不同步进电机所带动。根据被加工齿廓曲线的方程式，根据被加工齿廓曲线的方程式，可得出刀具中心轨迹方程，把它分解为沿X 轴方向的进刀及绕工件C轴的旋转两个分量，即可实现对齿廓的数控加工。

4.2.2刀具中心的轨迹
由上面可知，用数控加工齿廓时，应求出圆插刀中心的轨迹，它是被加工内齿圈齿廓曲线的内法向等距线，如图4.3所示。圆插刀的半径可不等于实际推杆减速器中滚子的半径，只要刀具半径T_d小于内齿圈齿廓在齿根部的最小曲率半径，在加工过程中不会发生切削干涉即可。对于激波器为偏心圆的推杆减速器，根据（2. 35）式，可得不发生切削干涉的条件为：

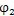
其中参数l₁、a₂与 关系为式（2.36）、（2.37）、（2.38）。

根据式（4.2）可算出数控插齿机所需的调整数据。

4.2.3数控编程
Y₅₄数控插齿机的数控系统经改进后，可直接与普通微机进行连接，通过微机上的一块接口电路板直接控制步进电机的驱动电路。因而，数控驱动程序可直接采用微机上的高级语言编制，其功能是将由刀具中心轨迹所得到的离散数据，经过一定的插补运算，变为驱动相应步进电机所需的脉冲数字信号，从而完成要求的加工任务。
提供给数控驱动程序的应是一组分别向x轴、C轴、D轴发出的脉冲数n_z、n_c、n_D，由数控驱动程序对这组脉冲进行线性插补运算，从而把输入廓形信息转化成步进电机运动的脉冲串。其脉冲频率由所要求的进给速度决定。
线性插补采用数值积分法（DDA)，其特点是运行速度快，脉冲分配均匀，易于实现多轴运动及绘制各种函数曲线。具体实现方法是：
选择位移量最大的轴为主导轴，即选取n_z、n_c、n_D三个数中的最大值作为脉冲溢出基数n_m，将n_x、n_c、n_D分别向各自累加器中累加，每累加一次判断各累加和是否大于溢出基值n_m，若大于，则给该轴发一个脉冲，同时从该累加器中减去溢出基值n_m，这样主导轴每次迭代时必有一个脉冲输出，其它两轴只有在满足条件时才有脉冲输出，经n_m次迭代后，各轴同时达到终点（向各轴发完各自的脉冲数）。

前面已求出加工内齿圈齿廓时刀具中心的轨迹方程，为了得到数控驱动程序所需的脉冲数据，还应将其曲线分成若干段，再求出每段中应分别向三个轴所发的脉冲数。
为此，首先应将式（4.2）化为极坐标形式

由于实际加工中是内齿圈绕其身中心轴（工作台C轴）旋转，而不是刀具绕C轴旋转，恨具只是沿x轴来回移动。因而为形成式（4.3）所示的曲线，极径P_d的变化由刀具沿x轴的变化来实现，极角θ_d的变化由内齿圈绕C轴的旋转来实现。

在曲线上取若干点，对相邻两点间的每一区段，极径和极角都有相应的增量△P_d及△θ_d转换成相应的脉冲数n_x及n_c。对于y₅₄数控插齿机，每个脉冲在x轴方向的进给量是0.004mm，在C轴及D上转动的角度都是15"，因而：

上式中假定θ_d的单位是弧度。
D轴的转动只是为了使刀具磨损比较均匀，并不是形成内齿圈齿廓所必须的运动。
具体编程时还应注意脉冲的正负是否和所需的运转方向一致以及加工时刀具的初始位置。
4.2.4机床调整
机床调整的适当与否，直接影响到被加工齿圈的质量。加工内齿圈齿廓时数控插齿机床的调整方法与在普通Y₅₄插齿机上加工内齿轮的调整方法大致相同。特别注意以下两点：
(1）内齿圈齿坯的安装与找正
内齿圈齿廓的数控加工，是在齿圈外径及两端面都精加工后进行的，因此，应以端面及外径作为定位基准。其夹具可做成螺钉压板结构，如图4.4所示。夹具内径应尽量接近齿圈外径，用千分表以夹具内圆为基准找正工作台轴心。

内齿圈在推杆减速器的机座中是靠定位健来固定的。因而其外径形有定位槽，装配时两个齿圈的定位槽应分别位于机座的左右两侧。为了使同一推杆减速器中两个齿廓形状完全相同的内齿圈能够互成180°布置，在齿廓加工前，先在齿圈外径上开槽，数控加工以此键槽为刀具定位基准。如图4.4所示，为了便于找正，在制作夹具时相应定位键槽制作一个定位基准平面，通过千分表很容易使其与x轴平行。
(2）对刀
在数控加工过程中，刀具中心距（刀具中心离工件回转中心的距离）反应的就是由式（4.3）所表示曲线极径，而在对刀时，初始中心距与曲线初始极径必须留有一定量的差距（一般为10mm～30mm)，这段径向差距留作数控加工一开始由刀具径向进给来完成。因而所留差距量应与数控程序中的相应数据相符合。

径向进给量要掌握适当，不能太大。齿坯一般为圆环形，为了不致使进给量过大，可分若干次进行加工，每次都可使用同一个数据文件，只需在每次对刀时，使刀具初始中心距作相应的增加。
与范成法相比，数控加工的优点是精度高，而且能做到使用同一把刀具加工不同规格的内齿圈齿廓，并能对刀具磨损进行补偿。其缺点是对于进行热处理后的精加工必须使用数控磨床。

4.3内齿圈齿廓的修形

4.3.1内齿圈齿廓修形的目标

由方程式（2.21）表示的内齿圈齿廓是无侧隙的，即圆周上所有的推杆，不论是否处于工作状态，都是和内齿圈齿廓相接触的。为了使推杆减速器便于装拆和保证良好的润滑，实际的推杆减速器不能采用这种无隙啮合的理论齿廓，而应采用有隙啮合的修形齿廓。修形齿廓就是有意识地将理论齿廓进行微量修削后所得到的齿廓。对齿廓修形除了给啮合传动留有一定量的间隙外，更重要的是使传动性能得到改善。所以修形齿廓的形状和参数是内齿圈齿廓加工的一个重要问题。

内齿圈齿廓修形后应达到的理想状态应该是：第一，齿廓顶、根部修形量要以避免齿顶、齿根部参于啮合，减小由于制造、装配误差造成的啮合冲击，提高啮合效率。第二，在齿廓中部修形量要小且尽可能均匀分布，并有较长的工作区，以保证有足够的同时啮合齿数，提高承载能力。第三，整个修形曲线要光滑，以保证机构运行平稳。

4.3.2参数增量修形法

由内齿圈的齿廓方程式可知，对内齿圈齿廓有影响的参数是推杆长度l，偏心圆激波器的半径T_b，偏心距e以及滚子半径T_Z0在数控加工中，分别对每个参数给以不同的增量，则所形成的齿侧间隙与范成加工中相应工艺数增量引起的齿侧间隙相同。因而单独对某个参数给以增量或同时给几个参数增量的不同组合，用计算机进行大量的计算，得到各种不同形式的修形曲线及其规律，可供设计者选择。

a.单一参数增量修形
等距修形：给参数T_Z一个增量△T_Z所得到的修形曲线是理论齿廓曲线的法向等距线。
移距修形：给参数l一个增量△1，或给参数T_b一个增量加△T_b，使被加工齿廓在原来理论情况下增加了一定量的进刀深度。
单独使用偏心增量助时，会在齿顶段或齿根段产生过盈，故不宜采用。

可见单一参数增量法修形效果离前面提出的齿廓修形目标相差太远，故常采用它们的组合修形。
b.等距移距修形
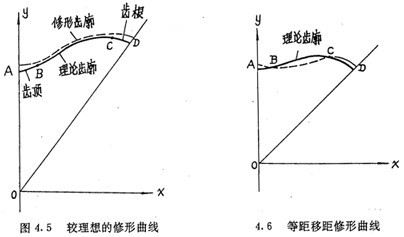
给参数T_z一负值增量（-△T_z)，同时给参数l-正值增量△l，计算表明修形曲线形状如图4.6中虚线所示。修形曲线实现了在齿顶，齿根修形量较大的目标（图4.6中的AB段及CD段），但要想在保持顶根修形量较大的前提下，在齿廓中段获得较长的工作区BC段，无论如何调整参数增量-△T_z及△l，都很难达到较理想的效果。对于其它组合修形，也有同样的问题。为此，需要研究一种更理想的修形方法。

4.3.3分段修形法
分段修形法是为了达到较理想的修形状态而提出的一种能够在数控加工中实现的齿廓修形方法。它根据修形后要达到的目标，将齿廓分成三段，如图4.7所示，在工作段BC内只进行微量的等距修形，在齿顶段AB及齿根段CD内同时进行等距△T_z和移距△l增量函数修形。

a.齿廓中段的修形
齿廓中段修形的要求是有较小且均匀分布的法向间隙。给参数T_z增量△T_z，可以达到这个目的。此时中段BC修形后的齿廓方程为：

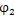
上式中l₁、a₂与 的关系仍为式（2.36）、（2.37）及（2.38），因为这些关系式中的T_Z为内滚子半径，故不变。中段修形范围是：

现在来证明齿顶修形曲线与中段修形曲线是光滑连接的。

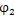
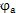
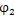
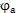
第一，在 = 处，两曲线连续。显然，当 = 时，l_a=l，a_2a=a₂，此时方程（4.8）就变成了方程（4.6）。

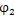
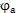
第二，在 = 处，两曲线有相同的切线。设齿顶段修形曲线的切线斜率为k_a，则由式（4.8）可得：

中段修形曲线的切线斜率k_m可由（4.6）式求得：

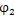
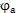
显然在 = 时，有k_a=k_m，即齿顶修形曲线与中段修形曲线光滑连接。

c.齿根段的修形

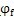
给定齿根修形角 和径向最大修形量△l_f，选择移距增量函数：

同样可以证明，齿根修形曲线与中段修形曲线也是光滑连接的。
4.3.4修形对工作推杆数的影响
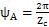
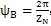
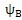
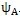
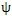
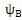
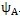
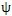
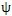
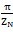
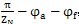
内齿圈齿廓修形之后，由于工作区域角的减小，使同时参加工作的推杆数也会有所减少。相邻两推杆之间的中心角为 ，而一个齿所对应的中心角为 ， 与 之差体现了相邻两个推杆相对所在齿廓初始位置的差异，记△ = - ，称△ 为位置差角，如图4.8所示。从图可知，工作推杆的数目等于推杆工作区域角与△ 的比值。推杆工作区域角指推杆从啮合传力开始到结束时推动传动圈转过的角度。在不修形的理论情况下，推杆工作区域角是 ，经修形后，顶根段不参与啮合，工作区域角为“θ= ，所以实际工作推杆数n_g为：

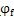
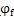
显然，未经修形的齿廓曲线在齿顶邻域和齿根邻域啮合的压力角都很小，因而分段修形后应将顶、根部大致削去相同的区段。即 、 仰的分配应根据各自所对应的顶根段曲线弧长相等的原则来进行。一般可近似取 为 的2到4倍，而取△l_f=esin 。

[计算实例]：

对于TW-3-16推杆减速器，要求内齿圈齿廓经修形后同时工作的推杆数n_g不少于5，按上述方法确定的修形量为：

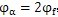
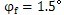
取 ，则 =3°， ，△l_a=0.36mm选择△T_Z=0.19mm，将齿廓分段修形后，机器性能得到了明显改善。

4.4内齿圈齿廓的公法线测量及加工精度控制

目前在推杆减速器的大批量生产中，对内齿圈齿廓的加工所采用的还都是范成加工方法，其测量手段长期以来一直没能得到很好的解决。一些生产厂家主要是利用测量齿根至齿圈外圆的厚度及齿顶至齿圈外圆的厚度来确定被加工齿廓的合格与否。这种方法并没有能够完全反应出内齿圈齿廓在加工过程中所产生的误差，它仅毙反应出偏心距的误差。公法线测量法是以预先计算出的公法线理论长度为依据，根据测量的结果，能够判断出加工过程中影响内齿圈齿廓加工精度的各个控制参数所产生的误差，从而对这些参数进行调整，使之达到要求的精度。

4.4.1公法线的长度计算
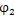
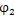
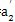
如图4.9 所示，AB是其中一个齿槽的一侧齿廓，A′B′是跨槽数为K（图中k=4)的一个齿梢的另一侧齿廓，它们是两个性质不同的齿廓。若把AB看成是工作齿廓，则A′B′是非工作齿廓。选择图4.9所示的坐标系，让坐标原点O与内齿圈几何中心重合，y轴与OA重合。设P（x，y）为AB齿廓上的一点，在P点与内齿圈齿廓相接触的外滚子的位置角为 ，在A′B′上取P点的对应点P′，使∠A′OO₂= ，P′点与P点是关于∠AOA′的平分线完全对称的，即0P′=OP，a₂= ，OO₁=00₂，图4.9中PO₁与P′O₂相交在Q点，它们并不共线，因此P′点与P点不具有共同的法线。假设随着P点位置的改变（当然P′点也随着P的改变而改变），使PO₁与P′O₂在同一条直线上，此时P′与P就有共同的法线，此时：

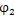
上式就是齿廓AB上与跨槽数为k的齿廓具有公法线的点的条件。当k确定后，若存在公法线，则由（4.17）式并结合基本关系式（2.38）等可解出 的值来。

从图4.9可求得公法线长度为：

              W_k=2（l₁+l）cosa₂+2r_z                                     （4.18）

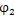
式中l₁、a₂与 的关系由基本关系式所确定。显然，两个齿槽的同侧齿廓（同为工作齿廓或非工作齿廓）是不存在公法线的。

4.4.2公法线的数目

由于内齿圈齿廓曲线具有周期性且工作齿廓与非工作齿廓是完全对称的，所以只需讨论一个齿槽的一侧齿廓与其它齿槽的另一侧齿廓所具有的公法线。

令：

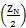
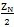
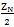
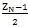
内齿圈的齿数Z_N可以是奇数，也可以是偶数（实际产品都是奇数）。为了讨论问题的方便，引用截断取整符号“INT”，当Z_N为偶数时，INT 等于 ，当Z_N为奇数时，INT 等于 ，由函数式（4.19）可得：

下面就来讲议化跨槽数k取不同数值时，具有的公法线情况：

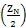
（1）跨槽数k≤INT 的情况

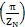
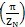
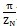
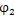
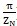
由（4.12）式及（4.22）式知，若Z_N为奇当选，有f（0）<0，f <0；若Z_N为偶数，有f（0）<0，f <0，因而不论Z_N是奇数还是偶数，方程（4.20）在区间[0， ]内若有解，则必为两个。为找出函数f（ ）在区间[0， ]内的极大点，令

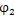
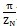
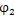
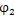
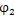
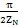
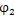
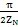
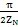
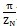
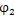
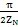
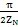
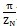
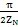
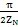
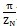
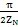
由上式结合基本关系式，利用计算机可解出 在区间[0， ]内f（ ）的极大点。显然，若极大值为正，则公法线有两条，若极大值为负，则公法线不存在。分析计算还表明，在极大点前，函数f（ ）单调增加，在极大点后，函数f（ ）单调减小。一般极大点接近 ，为讨论方便，选 =作特征点，代替极大点讨论，经计算证实，不会影响解的正确性。假若f() >0，则在[0， ]内必有两个点满足方程(4.20)，这两个点对应的 值分别位于[0， ]，（ ， 之内。结合图4.9可知，位于[0， ]内的点，其公线是凸齿公线，而位于（ ， 公法线凹齿公线。凸齿公线是被测两个齿廓上最短的连线，凹齿公法线是被测两个齿廓上最长的连线。这使得实际测量成为可行。假若f( )<0，则公法线不存在。

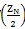
则当跨槽数k<k₀时，两齿廓不存在公法线。当INT ≥k>k₀时，两齿廓具有凸凹两条公法线。

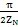
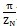
故方程（4.20）只在区间（ ， 内有解，即两齿廓只有一条凹齿公法线。

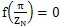
当Z_N为偶数时，有f（0）>0，,故两齿廓也只有一条凹齿公法线，且位于 =

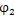
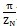
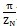
把跨槽数k取到k₀到INT() +1之间不同整数值时所具有的公法线合在一起就是内齿圈齿廓所具有的各种不同长度的公法线总数。

[算例]

对于前面提到的3TWY7.5-12推杆减速器，齿数Z_N=11，计算得到k₀=4，即当跨槽数k小于等于4时，两齿郭不具有公法线。当跨槽数k=5时，计算得到两条公法线，理论长度分别为：

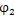
凸齿公法线   W₅₁=209.632mm，对应于 =1.755°

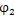
凹齿公法线   W₅₂=215.716mm，对应于 =12.485°

当跨槽数k=6时，计算得出只有 条凹齿公法线

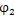
             W₆₃=230.146mm，对应于 =15.205°

合起来，此推杆减速器的内齿圈齿廓共有三条不同长度的公法线，它们的位置如图4.10所示。

4.4.3刀具轴线有偏距时的内齿廓及公法线

用圆柱形刀具加工内齿圈齿廓时，刀具轴线应在齿圈的半径方向作相对运动，如果它不沿着齿圈半径方向运动，那就有了偏距。在图4.11中，若刀具中心的运动方向平行于y轴，而刀具中心在O₂处，那就有了偏距E，现在来分析此时加工出来的齿廓及公法线长度，

同图4.11可得：

利用第二章中推导内外滚子工作角关系的方法可得a₂与a₁的关系为：

经过分析可知，当存在偏距E时，在跨槽数为k的两齿廓上具有公法线的点的条件仍然可用式（4.17）表示，公法线长度为：

若令（4.30）式和（4.31）式中的E=0，得到的就是无偏距时的内齿圈齿廓理论方程式（2.21）及公法线长度（4.18）式。

4.4.4利用公法线误差分析加工调整参数误差
由齿廓方程式（4.30）可以知道，齿廓形状取决于偏心轴的偏心距e，偏心轴几何中心到固定点长度R，刀具半径T_Z，进刀深度l以及刀具轴线偏距E。e和R是夹具结构上的固定尺寸，应该调整得尽量正确，而其误差加△e、△R也是个定值。而△T_Z是由于刀具制造误差及加工过程中的磨损引起，△l及△E是由于操作误差引起。因此，△T_Z、△l及△E是导致齿形误差的工艺因素。下面来分析它们对公法线长度的影响。

把公法线长度W_k看成是自变量为T_Z、l及E的函数，即W_k=W_k（T_Z，l，E），由（4.31）式可得：

假设用下标i表示公法线序号，用△W_ki表示第i条公法线实际测量出的值与理论计算出的值的误差，则可得到公法线长度误差方程为：

则：

上式中A^-1是矩阵A的逆阵，称误差矩阵。当算得相应的偏导数值后，如果测得一个齿槽的一侧齿廓与其它齿廓的三条公法线的误差，代入方程组（4.32）之后，便可求得相应的△T_Z、△l和△E。△T_Z是经计算得到的刀具半径的误差，△l是进刀深度误差，△E是刀具轴线偏心距的误差，根据计算结果适当调整这些参数就能迅速地提高齿廓精度，使之达到精度要求。

［计算实例〕
前面所说的3TWT7.5-12推杆减速器，根据参数可计算得到其误差矩阵A^-1为：

                  

在一个内齿圈齿廓上实际测得三条公法线的长度与理论长度的误差为：

△W₅₁=0.02261mm

△W₅₂=0.03806mm

△W₆₃=0.02106mm

代入式（4.32）可得：

△T_Z=0.0202mm，△l=0.032mm，△E=0.1697mm

根据计算结果适当调整这些参数就能迅速提高齿廓精度，使之达到精度要求。