钢丝绳弹悸联轴器大位移振动试验研究

2-1  引言

本章要进行式验研究的钢丝绳悸联轴器主要由内套、外套和六个钢丝绳弹性元件构件相连接组成，结构简图如图2-1所示，其中钢丝绳弹性元件构件如图2-2所示，它由绞合的不锈钢钢丝绳绕成的椭圆形正反向螺旋钢丝绳圈和上下夹持板组成，椭圆形螺旋形螺旋式钢丝绳绳圈之间的螺距相等。弹性元件在弹性联轴器中沿轴向Y均匀排列，X为联轴器切向，Z为联联轴器径向。弹性联轴器静态径向最大位移为±10毫米，平均刚度为：

K_Z=1.77×10⁶N/m                                 （2-1）

本试验的目的主要有以下几个，一是研究联轴器恢复力与振动频率和振幅的关系，为联轴器数学建模与参数辨识进行数据和理论准备，二是观察在大位移振动时，联轴器及弹性元件构件结构的变化，验证联轴器结构和弹性元件是否能在设计范围内正常工作，为今后设计联轴器积累实践经验。
我们选用正弦激励信号，频率变化范围选为l-30Hz，振幅变化范围为±（l-8）毫米。试验时，测量每一特定频率、振幅下的加速度、速度、位移和力的振动信号，为了保证有足够大的激励力在不同频率下使联轴器达到稳态周期大位移振动，选择适当的激励设备至关重要。
常用的激振设备是激振器或振动台。由BK产品目录可知4810，4809,4808和480lT，4801S,4802T,4802S等系列的激振器均不能满足上述要求，因此试图考虑用D350电动振动台来激励弹性联轴器。
2-2 D350电动振动台一联轴器系统振动试验的数字仿真
D350电动振动台的基本参数：最大振幅±12毫米（空载），频率范围5Hz-3000Hz，最大推力350公斤。

电动振动台一联轴器试验系统可表示为一个两自由度系统，振动微分方程为：

对应的力学模型如图2-3（见22页）所示，式中m₁为振动台动圈、联轴器外套及固定在振动台上夹具的质量；m₂为联轴器内套、芯轴及配重的质量；K₁为振动台支撑动圈部分的刚度系数，K₂为联轴器弹性元件的刚度系数；C₁为振动台动圈阻尼系数；C₂为联轴器
钢丝绳元件等效粘性阻尼系数。振动台给出的是正弦激励。
在确定（2-2）式中有关参数时，我们采用实侧方法，试验时所用仪器为：1.BK4370加速度传感器；2.BK25ll振动侧量义；3.BK1027信号发生器；4.D350电动振动台及功率放大器。

振动台刚度系数实测用静位移法，其测量步骤是首先将振动台面打气调平，加一重物W_i，用百分表测得台面下沈静变形δ_i，算得对应的刚度系数K_i=W_i/δ_i，如此反复加十块重物，算得十个对应的刚度系数，由此可得振动台的平均刚度系数K₁。

实测动圈质量m₀时，置振动台动圈推力一定值F，空载测得振动台动圈质量m₀的加速度 和位移，此时，将D350电动振动台考虑为一个单自由系统，运动生分方程为（由于振动台动圈阻尼一般较小，故不考虑C₁的作用）：

然后，在振动台上加一质量m_a，测得动圈加速度 和位移x_a，维持推力不变，此时，加速度可表示为：

然后取下质量m_a，维持推力不变，在振动台上另加一质量m_b，重复以上试验，由式（2-7）算得m₀，将两次试验所得m₀取平均值，得到圈质量。

弹性联轴器钢弹性元件的阻尼系数用一个等效粘性阻尼系数代替，根据一个振动周期内非粘性阻尼和等效性阻尼消耗的能量相等原则来计算。从弹性联轴器静态试验所得的迟滞回线可得联轴器径向等效粘性阻尼系数为：

C_eZ=330/πω          （N·S/mm）                                （2-8）

在进行弹性联轴器一电动振动台系统的计算机数字仿真振动试验时，内套及芯轴质量一定，

配重重最在0～20公斤范围内变化，以保证试件总重量不超过振动台50公斤承重能力的限制。由于电动振动台动圈的阻尼很小，因此在仿真计算时取动圈的振动阻尼C₁为零，激励力的频率变化范围为5Hz～2KHz。
分析振动试验的计算机仿真计算结果后可以得出以下结论：1.当配重一定时，随着撇励频率的增加，m₁与m₂之间的相对位移由大变小（配重等于3公斤的情况除外）逐步趋于零；当频率等于310Hz以后，相对位移幅值等于零。2.当频率为5Hz时，随着配重的增加，相对位移增加，但即使配重达20公斤极限时，相对位移幅值仅为0.2048毫米，远不能满足8毫米的要。3.当频率为1OHz时，相对位移幅值开始趋于相等，而不随配重重量变化而变化，随着频率的进一步增大，相对位移幅值完全相等，变化规律见图2-4所示．由此可见D350电动振动台的基本参数范围内，加不同的配重均不能使联轴器振动系统满足试验要求（即振幅应为±（8-10）毫米）。

2-3 MTS材料试验机振动试验功能的开发及联轴器大位移振动试验

由于常规的激励方式无法满足钢丝绳联轴器振动试验的要求，我们不得不另辟途径。MTS材料试验机一般用于材料的应力应变、强度以及疲劳试验，其位移一般不超过1毫米，但此材料试验机具有往复运动的功能，因此尝试利用它作为激振器，对大挠度弹性联轴器进行振动试验，试验系统如图2-5所示。MTS试验机主要由机架、上下夹头、油缸活塞和控制器等组成。控制器能精确地控制试验机上下夹头往复运动的频率、振幅和振动位移的波形。弹性联轴器由我们专门设计的夹具与MTS试验机的上下夹头相连接，夹具保证联轴器在径向振动时，所受拉压力的作用线与弹性联轴器在受力方向上的对称几何中心线重合。
正弦位移激励频率和振幅由MTS控制器编程控制。正弦位移激励频率的变化范围为IHZ到3OHz，振幅的变化范围为±1毫米至±8毫米，振动的位移、速度和加速度分别用三个加速度传感器进行测量，同时用MTS试验机自带的位移传感器和力传感器测量振动位移和力的信号。前三路信号经电荷放大器后输人磁带记录仪，后两路信号由MTS控制器中自带放大器再输出到磁带机记录，同时榆到双线示波器以供监视。

2-4测试信号的处理和分析

信号处理时，将磁带记录仪记录的五路振动信号经磁带记录仪回放，愉出到数据采集板（A/D板）进行五路振动信号（恢复力、位移、速度、加速度信号）同步采样和A/D转换，然后输出到PC386微机存人磁盘，该数据采集系统采集的数据都是以二进制形式存储的文件。为了计算和阅读方便，需将二进制数据文件转换成ASC码文件，然后再编程进行数据处理．对处理后形成的数据文件进行作图可以形成许多相应的曲线图，图2-6至图2-13是众多曲线中的一部分。

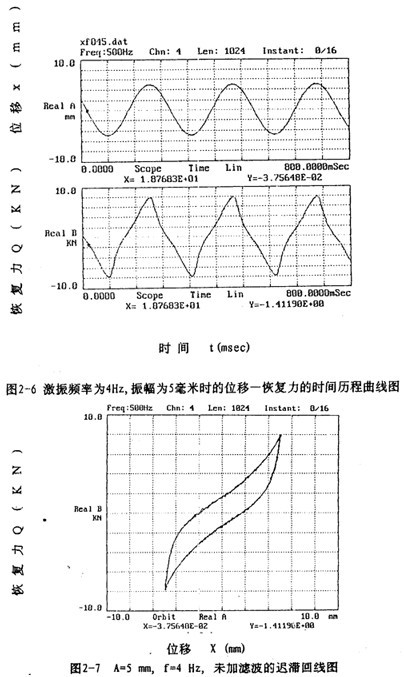
图2-6表示激振频率为4Hz，振动位移幅值为±5毫米的位移和恢复力的时间历程曲线图，由图可知，位移时间历程为正弦波形，对应的恢复力时间历程为近似的锯齿波形。以位移为横坐标，恢复力为纵坐标，图2-6对应的位移恢复力图为图2-7,由此图可知弹性联轴器具有非线性迟滞特性。在动态情况下，由于机座的高频振动和环境干扰等因素，试验记录的信号中有高频成分存在，这使得迟滞回线不光滑，加低通数字滤波后可得光滑的迟滞回线，如图2-8所示。

图2-9（见26页）表示激振频率为1OHz，振动位移幅值为±2毫米的位移和恢复力时间历程图，图2-10（见26页）、图2-11（见27页）为对应的迟滞回线图。图2-l2（见27、28页）表示激振频率为IHz，振动位移幅值分别为±（1-8）毫米的位移一恢复力图，图2-14（见29页）则为图2-12的合图，由图2-14同频率不同振幅的八条迟滞回线分析可知，大挠度刚丝绳弹性联轴器的动刚度与振动幅值有关，同时，从迟滞回线面积（表示联轴器阻尼所耗散的能量）可知联轴器的阻尼与振动幅值也有关，即联轴器的动刚度和阻尼均是振幅的非线性函数。
图2-13（见28、29页）表示振幅为l毫米，激振频率分别为2,3,4,6,8,10Hz的迟滞回线图，图2-15（见29页）表示振幅为1毫米，激振频率为1,2,3,4,6,8,10,20,30Hz的迟滞回线合图。由图2-15可知，弹性联轴器的动刚度与振动频率有关，即随着频率增大，对应的迟滞回线的恢复力与位移的比值变小，当频率在8Hz至30Hz范围内时，迟滞回线基本重合，由此可知钢丝绳联轴器动刚度在一定频率范围内与频率有关、当频率增大到8Hz以后，联轴器的动刚度不再随频率变化而变化，因而联轴器的动刚度在一定频率范围内是频率的非线性函数，当频率增大到一定值后，动刚度与频率无关。同样，联轴器的阻尼在一定频率范围内是频率的非线性函数，当频率增大到一定值后（这里是8Hz)，阻尼与频率无关。

 

2-5小结

通过对钢丝绳弹性联轴器的振动试验、信号处理和分析，可以得到以下结论：

1.开发MTS材料试验机对大挠度弹性联轴器进行大位移振动试验是可行的，解决了激振器或振动台不能同时满足大位移、频率和激振力达到一定要求的难题，为大位移振动试验开辟了新的途径。
2.钢丝绳弹性联轴器能产生动态大位移，具有补偿主机在运行中出现大位移的能力。联轴器及钢丝绳弹性元件能在设计范围内正常工作，但有的弹性元件出现钢丝断丝现象，夹持板在低频大位移振动时变形较大，因此有必要对弹性元件的联接方式进行改进。
3.钢丝绳弹性联轴器的恢复力具有非线性迟滞特性，在大位移振动情况下表现出动刚度非线性和阻尼非线性的特性，联轴器的动刚度是振动幅值和频率的非线性函数，但当频率增大到一定值后，动刚度仅为振幅的非线性函数。同样，联轴器的阻尼在一定频率范围内是振幅和频舞的非线性函数，但当频率增大至一定值后，阻尼仅是振幅的非线性函数。因此大挠度弹性联轴器的本构关系是一非线性泛函。

4.以上研究成果为联轴器恢复力数学模型的建立、参数辨识提供了依据和准备了数据。