具有非线性迟滞特性钢丝绳联轴器建模与参数辨识

3-1引言

由上章对联轴器振动试验研究结果可知，在大位移振动情况下，联轴器表现出非线性迟滞特性．这一特性直接与联轴器动刚度及阻尼有关，当这种联轴器用于船舶推进轴系时，将影响到轴系的动力特性，因此弄清楚联轴器恢复力与动刚度和阻尼的关系，即建立联轴器恢复力的数学模型是十分重要的，对于深人分析研究推进轴系的动力特性也是不可缺少的。
由钢丝绳联轴器的 -x迟滞回线可知，联轴器的迟滞特性不宜用双线性模型来描述，主要原因是双线性模型与联轴器的动态迟滞回线外形相差甚远，双线性模型将系统刚度系数处理成二个线性刚度系数。这不足以描述钢丝绳联轴器的非线性迟滞特性中的非线性刚度系数，双线性模型阻尼仅处理为干摩擦阻尼，也不足以描述联轴器阻尼的复杂成分。一阶微分方程模型主要用于迟滞系统的随机响应分析中，这种模型用于计算迟滞系统的稳态动力响应很不方便，模型中各参数的物理意义不明确，模型形式不利于各参数的辨识，而且弹性力和阻尼力在恢复力表达式中不显现，不利于理论分析。基于平均和等效原理的迹法和以此为基础K₀等建立的模型都有自己的不足，前者只能描述迟滞恢复力与位移和速度的关系，而不能全面描述迟滞恢复力与各振动参数的关系，后者只能描述三个阶次非线性弹簧刚度，其应用范围受到限制。由此可知，现有描述迟滞特性的数学模型都不能用来描述联轴器的非线性迟滞特性。因此，本章将在前人研究的基础上，研究联轴器动刚度和阻尼的特性，建立既能合理描述联轴器非线性迟滞特性又能满足较高精度要求的数学模型。

3-2拟合分解恢复力一位移迟滞回线

上一章的试验研究表明，钢丝绳弹性联抽器的本构关系十分复杂，其恢复力是联轴器动刚度和阻尼的函数，而动刚度和阻尼又是振幅和频率的函数。因此，我们将依靠试验获得的测量数据，在迹法和文献的基础上，深人研究联轴器迟滞特性，建立联轴器的数学模型。
由前面联轴器位移一恢复力试验可知，迟滞回线可以分为上、下两条，分别对应于速度大于零和速度小于零。在钢丝绳弹性元件性质相同和安装几何对称的情况下，上、下两条恢复力曲线可以认为是位移反对称的。于是可以用幂函数多项式，按最小二乘法原理来拟合代表试验数据的上、下两条恢复力曲线，设用于拟合上迟滞回线数据的幂函数多项式为：

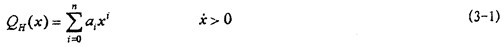
根据反对称，用于拟合下迟滞回线数据的幂函数多项式为：

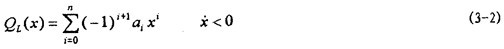
式中，_H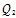， 分别为联轴器迟滞恢复力上、下曲线，x为位称，a_i为幂函数多项式系数。

幂函数多项式所取项数n按拟合的迟滞回线形状和对表达式要求的精度而定。将（3-1）和（3-2）式中幂函数多项式的奇、偶次项分开写，可进一步表示为：

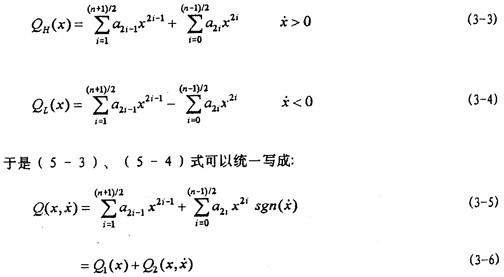
经以上数学处理，联轴器的动态迟滞回线可以分解成₁（x）和 ₂（x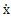， ）两部分，即联轴器的迟滞恢复力由两部分组成。戒n取奇数。从几何意义上讲，第一部分为一条单值非线性函数曲线，第二部分为一条双值的非线性闭合曲线。从物理意义上讲，第一总值发代表迟滞恢复力中的非迟滞非线性弹性恢复力；第二部分代表迟滞恢复力中的纯迟滞非线性阻尼力。

由试验知，联轴器的迟滞恢复力不仅是位移x和速度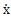的函数，而且还是振幅A和频率ω的函数，因此识滞恢万力的教学模形没为：

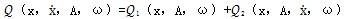        （3-7）

由此可见，迟滞恢复力的函数关系相当复杂，

由试验还可以知道，频率增大至一定值后动刚度和阻尼仅是振幅A的非线性函数，在这种情况下，迟滞恢复力的数学模型可表示为：

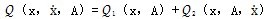             （3-8）

由此，我们得到两种形式的联轴器恢复力数学模型，前者为考虑频率影响的数学模型，后者为不考虑频率影响的数学模型。

至此，尽管我们将迟滞恢复力拟合分解成了两部分，但是_l和₂取什么样的函数形式，仍然是一个难题。对此，分三步来研究。第一步先求出不同频率和振幅下迟滞数据回线的拟合迟滞回线，得到对应的各阶离散的刚度系数值，以及迟滞阻尼耗能值；第二步再找出这些数值与频率、振幅的函数关系表达式，从而得到_l和₂的函数关系表达式，第三步，通过参数辨识，寻找出_l和₂表达式中的各参数。

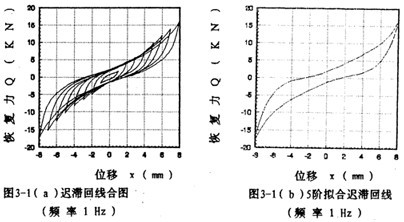
由迟滞回线的形状可知，联轴器具有强非线性的特性，为了在数学模型中反映出强非线性的特性，选9阶幕函数多项式来拟合上、下迟滞回线（n=9)，对一定频率和振幅的每一组试验迟滞回线数据，由线性最小二乘法原理一辨识对应的各阶拟合系数。对图2-14中各迟滞回一数据进行拟合，将所得的拟合迟滞回线与图2-14的迟滞回线画在一起，如图3-1（a）所示，由此图可知，两者重合性很好。

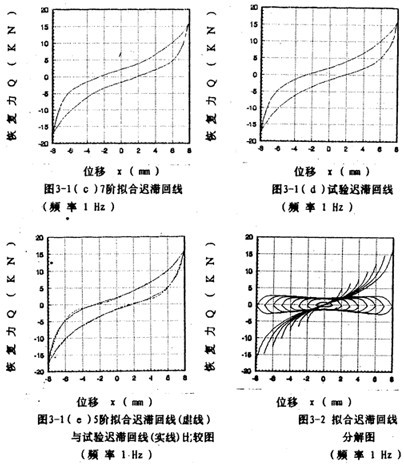
为了说明5阶和7阶幂函数多项式拟合的精度情况，以振幅A=8毫米，频率为1赫兹为例，画出拟合回线分别如图3-1（b）、3-1（c）所示，将它们与对应试验回线图3-1（d）比较，可知7阶拟合精度高于5阶。图3-1（e）为图3-1（b）与图3-1（d）的合图。

为了得到（3-6）式所示的_l，₂，将拟合得到的各幂函数多项式奇、偶次项分开写成（3-5）式形式并作对应的曲线图，如图3-2（见34页）所示，它样就将恢复力分解成了单值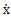非线性函数曲线和双值的非线性函数闭合曲线，由此得到了对应的_l（x）和₂（x，）的若干组函数表达式：

式（3-9）中各系数a_2i-1实质上代表联轴器弹性恢复力在对应频率、振幅下的各阶刚度系数。

3-3联轴器数学建模

一、不考虑频率影响的数学模型

由于联轴器恢复力仅在一个小范围内受频率的影响，当频率达到一定值后，联轴器恢复力仅是振幅的函数，在这种情况下，数学模型的表达式为（3-8）式。下面分别研究_l和₂函数表达式的结构形式。

1.非迟滞非线性弹性恢复力_l的数学模型

在不考虑频率影响的情况下，联轴器弹性恢复力，由以上分析，可以建立其数学模型如下：

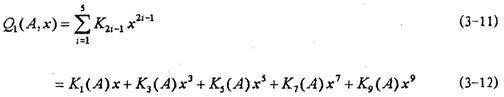
式中K₁（A）--K_9­（A）是钢丝绳联轴器第一～九阶弹簧刚度函数。

这样的数学模型充分地考虑了高阶非线性弹性力的影响。式中K_2i-1（A）仅是振幅的函数，其数学模型为：

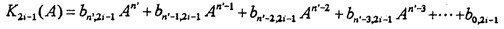（i=1，2，3，4，5）                                 （3-13）

式中n′根据精度要求而定。

2.迟滞非线性阻尼力₂的数学模型
由拟合迟滞回线分解图3-2中各闭合曲线知，联轴器中的阻尼成分非常复杂，有可能是多种阻尼的组合，根据联轴器弹性元件变形及工作情况，可以认为联轴器阻尼含有粘性阻尼和干摩擦阻尼的成份较多，因此，在这种情况下我们建立以下二种阻尼力模型：

(1）复合型阻尼力模型

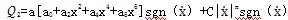              （3-14）

式中第一项代表除粘性阻尼力和干摩擦力以外的其它阻尼力成份，系数a决定这些阻尼力所占比例，故定义为阻尼比例控制系数；第二项代表粘性阻尼力和干摩擦阻尼力综合阻尼力成份，当n=o时，这项为Csgn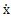（），代表干摩擦阻尼力，当n=1时，这项为C|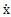|sgn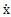（），代表粘性阻尼力，当n在（0，1）区间变化时，第二项代表的是粘性阻尼力和干摩擦阻尼力的混合阻尼力，系数n决定两种阻尼各占份额多少，定义为粘摩阻尼分配系数。式中a₀,a₂，a₄，a₆，C,n和a均是振幅的函数。

(2）等效粘性阻尼力模型
用等效粘性阻尼来描述迟滞非线性阻尼，其恢复力构建为：

₂=C（A，ω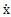）                                    （3-15）

由于联轴器阻尼成份的复杂性，以上建立的二种阻尼恢复力模型中哪一种用来描述联轴器阻尼力更为合理，有待于参数辨识后才能确定。对于模型（3-14)，我们将先辨识出在不同振幅下模型中的各个参数，然后再找出这些参数与振幅的函数关系。对于模型（3-15)，我们将根据一个振动周期内迟滞非线性阻尼所耗散的能量与等效粘性阻尼所消耗的能量相等的能量关系找出等效粘性阻尼函数C(A，ω）与振幅和频率的关系。

二、考虑频率影响的数学模型

在这种情况下，联轴器的数学模型的表达式为（3-7）式，下面分别讨论_l和₂函数表达式的结构形式：

1.非迟滞非线性弹性恢复力_l的数学模型

由试验研究知道，联轴器的弹性恢复力不仅是振幅的的函数而且还是频率的函数，随着频率的增大，在一定频率范围内，弹性恢复力逐渐减小，然后趋于一定值，根据这一特性，在建造弹性恢复力新的数学模型时，引进一个能描述这一特性的指数函数项e^-flr（f），这样，新构建的弹性恢复力数学模型为：

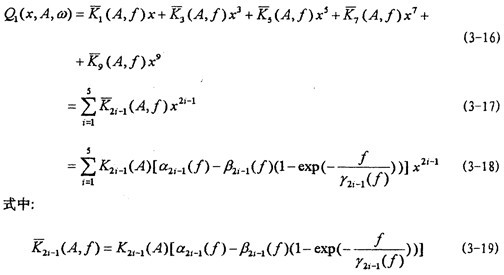
同时，定义几个新函数参数，a_2i-1（f）为刚度幅值频率影响系数，它表示联轴器弹性元件各阶刚度的幅值受频率变化影响的程度；β_2i-1（f）称为刚度幅值频率衰减系数，表示弹性元件各阶刚度的幅值随频率增加的衰减程度；y_2i-1（f）称为刚度频率衰退减系数，表示弹性元件各阶刚度随频率增加的衰减速率，y_2i-1（f）愈大，刚度值随频率减小的速度就愈慢，反之，则愈快。从理论上讲，只有当f值趋于无穷大时，exp{-f/[ y_2i-1（f）]}才趋于零，各阶刚度 _2i-1（A，f）才趋于各自的定值K_2i-1（A）[a_2i-1（f）-β_2i-1（f）]。但事实上，由于指数曲线开始变化较大，而后逐渐缓慢，所以，实际上f达到一定值后，exp{-f/[ y_2i-1（f）]}已经很小了，例如，设f=5 y_2i-1（f），这时有：

y_2i-1（f）= K_2i-1（A）[a_2i-1（f）-β_2i-1（f）（1-e^-5）]

= K_2i-1（A）[a_2i-1（f）-β_2i-1（f）×0.99326]                                （3-20）                                                                                                          

当频率f=8，10，…，30赫兹时，刚度不再随频率的变化而变化，由此可得y_2i-1（f）=1，6,2，…，6；a_2i-1（f）-β_2i-1（f）×0.99326=β_c，这些参数值和关系式在辨识（3-19）式中参数时，可作为已知条件应用。
从以上分析可知，(3-18）式表示的数学模型能客观地反映联轴器弹性恢复力随振幅和频率变化的规律。

2.迟滞非线性阻尼力姚的数学模型
当同时考虑振幅和频率对迟滞阻尼力₂的影响时，₂将是振幅和频率的函数，如果经过参数辨识说明（3-14）形式的数学模型能合理地描述阻尼力，那么，在同时计及振幅和频率对迟滞阻尼力姚的影响时，我们仍建立迟滞阻尼力的数学模型表达式为（3-14）式的形式，不过其中各系数不仅是振幅A的函数而且还是频率f的函数，建立的第二种数学模型仍以等效粘性阻尼来描述迟滞非线性阻尼，与(3-15）式所不同的是，在此建立联轴器阻尼耗能的函数时，同时考虑联轴器迟滞回线面积随振幅A和频率f变化的规律，而在建立（3-15）式时仅考虑联轴器迟滞回线面积随振幅A的变化规律。为了叙述方便，这些问题在参数辨识一节中讨论。这样，这二种阻尼力模型为：

结上所述，将（3-12）式与（3-18）式比较，将（3-14）～（3-15）式与（3-21）～（3-22）对应式比较可知，后者同时考虑了振幅A和频率f对联轴器恢复力的影响，因而适用范围较前者仅考虑振幅A的影响时更大，但后都数学表达式复杂，大大地增加了参数的辨识难度。由试验研究知，频率变化为恢复力影响范围较小，为了简化计算用（3-12）和（3-14）～（3-15）较好。

3-4联轴器数学模型参数辨识

本节将利用试验数据，根据上节建立的联轴器恢复力数学模型的类型，分别选用线性参数辨识方法和非线性参数辨识方法，按最小二乘法原理，辨识联轴器数学模型中的参数，找出各参数与振幅和频率的关系，得到联轴器恢复力由弹性和阻尼力描述的函数关系式。

一、参数辨识的难点
联轴器数学模型函数关系的复杂性以及函数关系式中参数的非线性都给参数辨识工作带来困难。针对这些情况，对数学模型中某些参数随振幅和频率变化规律还不能给出表达式时，我们先求出这些模型在不同振幅和频率下，各参数随振幅和频率变化的离散值，然后根据这些离散值随振幅和频率变化的规律，来定出函数表达式，在此基础上再进一步找出这些参数与振幅和频率的函数关系，最后得到联轴器恢复力与振幅、频率、位移和速度的表达式。

二、参数辨识
1.辨识不考虑频率影响数学模型的参数
不考虑频率影响时联轴器的数学模型为（3-12）～（3-15）式，

a.非线性弹性恢复力_l数学模型中参数的辨识
此中情况下，_l的表达式为（3-12）和（3-13）式。由这两式可知，模型中含有九阶的高次非线性弹性力，其各阶动刚度K_2i-1 (A）是振幅的函数，数学模型为一个n′阶的幂函数多项式，K_2i-1 (A）是各参数b_0，2i-1～b_n，2i-1 (i=1,2，…，5）的线性函数。于是各阶动刚度K_2i-1 (A）中各参数辨识可归结以下最小二乘法问题：

已知K_2i-1 (A）是关于自变量X=[A，A²，…Aⁿ¹]^T和待定参数B=[ b_0，2i-1，b_1，2i-1，…，b_n′，2i-1]^T的形式已知的函数（3-13)，简写成：

 K_2i-1 (A）=f（X，B）                （3-23）

今给出（X，K_2i-1 ）的n对试验值：

（X_K，K_2i-1，K）     （k=1，2，…，n）    （3-24）

要求确定参数B使

得一组线性方程组，在n>k的情况下，联立求解这一线性方程组即可求得唯一的一组B值。根据此法求得（3-13）式中参数值并代回可得:

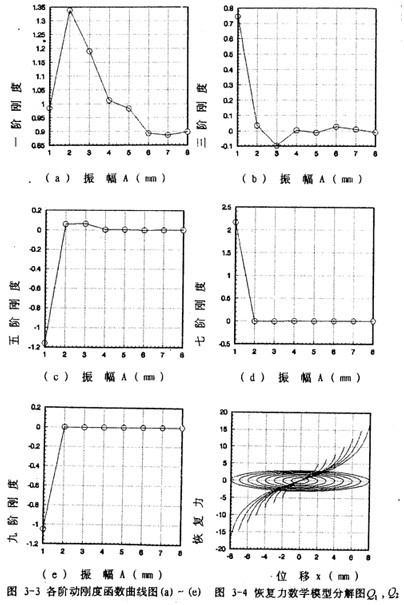
将（3-27）式中刚度函数作成曲线如图3-3(a）-（e）所示，由一阶动刚度函数图3-3(a）可知，振幅在lmm～2mm范围内时，动刚度随振幅增大而增大，呈硬特性；当振幅在2mm～7mm范围内时，动刚度随振幅增大而减小，呈软特性；当振幅在7mm～8mm范围时，动刚度随振幅增大略有回升。由此图可知，在联轴器初始小振幅和极限振幅附近范围内，动刚度呈硬特性，而在中间振幅范围内呈软特性。K₅（A）和K₉（A）也具有类似的特性。而K₃（A）和K₇（A）在小振幅时呈软特性，这样的动刚度特性满足船舶缓冲减振降噪的要求，即在一般低能量风浪流作用下，该联轴器钢丝绳元件的变形小，动刚度大，呈硬特性，这能保证船舶推进轴系的基频高于风浪流的显著能量频率；在大能量风浪流和冲击作用下时，联轴器由于载荷增大而变形增大，这种情况下动刚度软化，使船舶推进轴系频率变小，向远离大能量风浪流和冲击显著能量频率一侧偏移，在迟滞阻尼下耗散能量，使轴系冲击振动响应降低。由（3-27）式和（3-12）式可作出相应的弹性恢复力单值曲线如图3-4所示。将图3-4中代表弹性恢复力的单值曲线与图3-2中的单值曲线比较可知，(3-12）式能较好地描述联轴器弹性恢复力随振幅变化的规律。

b.非线性阻尼力数学模型中参数的辨识

此情况下，建立了二种数学模型（3-14）式和（3-15）式。对于（3-14）式描述的模型，₂是参数n的非线性函数，因此，在进行参数辨识时，需要用非线性参数的辨识方法。此时，这种模型中各参数的辨识可归结为如下的最小二乘法问题：

已知₂是关于自变量X=[x₁，x₂，…，s_p]^T和待定参数B=[b₁，b₂，…，b_m]^T的形式已知函数（3-14）式，简写成：

₂=f（X，B）                            （3-28）

对于给定的n组试验数据值（X_k，_2k），要求确定参数B使

为最小。对于这种非线性参数识别，很难直接进行求解，通常采用逐次逼近的方法处理，在此采用高斯-牛顿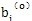法来辨识。高斯-牛顿法的基本思想是：先给出各参数b_i的一个初始值，记为           ，初值与真值之差为△_i，即有：

b_i= 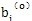          +△_i             （i=1，2，…，m）                           （3-30）

这样，确定b_i，在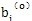邻域内将函数f（X，B）作代台劳级数展开，并略去△_i的二次及二次以上项得：

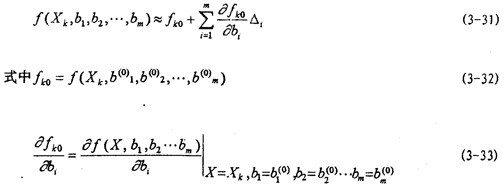
当 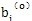        给定时，f_ko和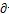f_ko/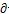b_i都是自变量X的函数，可直接算出，将（3-31）式代入（3-29）得：

由多元函灵敏极值存在的必要条件：

得以△_i为未知量的一组m个联立方程组

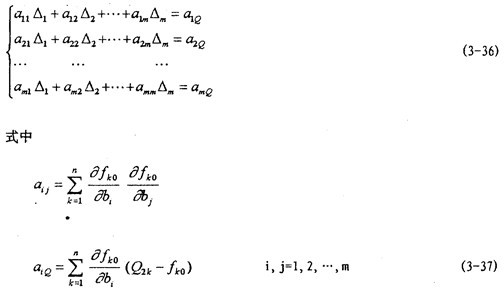
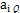当试验数据值（X_k，_2k），（k=1，2，…，m）给定后，系数a_ij及均可算出，因此由方程组可解出△_i，进而得b_i­的值。当算出的|△₁ |值较大的时，可令当前的b_i值代替原来的初始近似值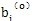，重复计算a_ij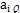，，并解方程组（3-36）得新的△_i，进而得b_i。这种过程可以重复进行，直至|△_i |的值小到给定的精度为止。

对于非线性参数辨识问题，并在不于迭代工作量有多大，而是在迭代逼近过程中是否收敛，即迭代过程有可能不按上述方式完成，出现计算溢出，方程组系数矩阵病态等毛病．出现这些问题的原因大致有三种：一是逼近试验数据点（X_k，_2k）的数学模型假设与数据点甚远，在这种情况下，必然重新分析系统的内在机理，建立符合系统特性的新数学模型；另一种是初值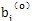选得不好，台劳级数展开式完全失真，迭代得到的新b_i有可能比原来的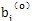更远离真解，且越迭代越糟糕，最后发散，在这种情况下，迭代是否收敛，关键在于初值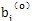的选择；第三种是参数辨识的算法不适合或对初值选取的要求太高，在这种情况下，需选择更合适的算法或选择对初值选取要求较低的算法。
按照以上算法，编制了计算机软件对（3-14）模型中的参数进行了辨识，结果讨论如下：
对（3-14）模型，用不同振幅下联轴器试验数据中代表阻尼力的数据来进行参数辨识，辨识结果是迭代计算不收敛，分析其原因，我们认为，一是因为需辨识的参数较多，初始值不易选得与真值较接近，致使迭代不成功；二是此算法可能不适合此模型的参数辨识。因此，有待于寻找能辨识数学模型表达式中参数的新的有效辨识方法。
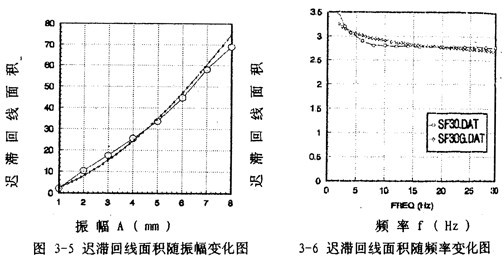
第二种模型是（3-15）式，在这种情况下，用阻尼耗能的能量关系来辨识阻尼力与振幅等参数的关系。由图3-1可知，联轴器每振动一周所消耗的能量，即迟滞回线的面积S是振幅A的函数。由数值积分，可以算出各振幅变化时迟滞回线面积，由此可得迟滞回线面积与振幅的一一对应关系，将这些一一对应的数据点画成图，如图3-5中大圆点曲线所示，由此分析迟滞回线面积随振幅变化的规律，可建立其函数关系为：

S_ga（A）=a_sA^bs                             （3-38）

式中a_s和b_s为待辨识参数。由（3-38）可知，面积是参数b_s的非线性函数，参数辨识时用非线性参数辨识方法，高斯一牛顿法，辨识结果为a_s=2.56969，b_s=1.62309，代回（3-38）式并画出曲线如图3-5中小点曲线所示。由此可以看出，(3-38）式能较好地描述迟滞回线面积（即联轴器阻尼耗能）随振幅变化的规律．在用等效粘性阻尼来代替迟滞非线性阻尼的情况下，在具有相同振幅的正弦振动时，每周由等效粘性阻尼力耗散的能量为：

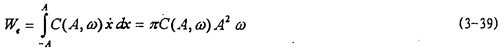
因为S_ga=W_e，由（3-38）与（3-39）可得联轴器阻尼函数C（A，ω）：

将（3-40）式代入（3-15）式得联轴器阻尼力模型：

值得注意的是此阻尼力模型的参数辨识是在研究阻尼耗能过程中，仅考虑振幅对耗能的影响下得出的，而没有考虑频率对耗能的影响，式中频率项的出现是由于用等效粘性阻尼代替迟滞非线性阻尼所致。将（3-41）式画成曲线得图3-4中每椭圆，与图3-2中的闭合曲线相比较可知（3-41）式较好地描述了迟滞非线性阻尼力。将（3-11）、（3-27）和（3-41）式代人（3-8）式即，得联轴器恢复力数学模型的函数表达式。

2.辨识考虑频率影响数学模型的参数
考虑频率影响时联轴器的数学模型为（3-17）-（3-22）式。

a.非线性弹性恢复力Ql数学模型中参数的辨识
此情况下，₁的表达式为（3-18）-（3-19）式，由于数学模型中参数辨识的复杂性以及待辨识参数的非线性性，在辨识过程中，先辨识出在不同振幅和频率下模型中的各参数a_2i-1，β_2i-1和y_2i-1，然后根据这些参数离散散值随频率变化的规律，建立它们与频率之间的函数关系，再辨识这些函数关系式中的各参数，从而得到a_2i-1 (f)，β_2i-1（f）和y_2i-1 (f）的函数表达式，最后得到动刚度 _2i-1（A，f）随频率和振幅变化的数学模型和弹性恢复力教学模型。

我们用高斯-牛顿法的最小二乘法来辨识，辨识结果是迭代计算不收敛，分析原因认为：迭代计算不收敛，一是初值选择不合理，二是此算法对初值要求太高。尽管如此，但根据对联轴器非线性弹性恢复力随频率变化的规律分析，我们仍认为用（3-18）式来描述联轴器弹性恢复力_l=（x,A，ω）是客观的和合理的，式中未知参数的辨识有待于寻找新的有效的辨识算法。

b.非线性阻尼力乌数学模型中参数的辨识

此情况下，建立的数学模型为（3-21）-（3-22）式。对（3-21）式，辨识所用方法和试验数据与辨识（3-14）式相同，所得结果是迭代计算不收敛，究其原因, 认为是所用辨识算法不适合此模型的参数辨识，同时此算法对初值的要求比较高。

为了解决以上未决的参数辨识问题，我们又用了一种算法，Marquardt算法对（3-14）、（3-18）和（3-21）模型进行了参数辨识，迭代计算仍不收敛。为了解决这一问题有待进一步寻找有效的辨识算法。

对于（3-22)模型，我们用阻尼耗能的能量关系来辨识阻尼力与振幅和频率的关系。在前面，迟滞回线面积（即阻尼耗能）与振幅的函数关系已建立起来，见（3-38）式，而且式中参数也已辨识出。同样，用数值积分，可以算出振幅一定，频率变化时迟滞回线的面积，由此得出迟滞回线面积与频率的对应关系，将这些对应关系画成曲线如图3-6中大圆点曲线所示。由迟滞回线面积随频率变化的规律分析，可建立其函数关系为：

S_gf（f）=a_ff^bf                              （3-42）

式中a_f和b_f为待辨识参数。由此式知，面积是参数务的非线性函数，用高斯-牛顿法辨识得a_f=3.40234,b_f=-0.0684433，代回（3-42）式并画曲线如图3-6中小点曲线所示。由此可知，(3-42）式能较好地描述迟滞回线面积随频率变化的规律，阻尼耗散的能量随频率的增大而减小。综合考虑（3-38）和（3-42）式中阻尼耗散的能量随振幅和频率变化的规律可知，阻尼耗能随振幅的增大而增大，随频率的增大而减小，由此可建立联轴器阻尼耗能（即迟滞回线面积）随振幅A、频率f变化的数学模型如下：

式中a_g,P,q为待定参数。由此式可知，联轴器阻尼耗能是振幅和频率的非线性函数也是参数p,q的非线性函数。在辨识时，采用高斯-牛顿法。根据（3-38）、(3-42）两式及其参数，可知（3-43）中a_g参数的变化域在（2.56969,3.40234）内，q值在1.62309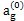附近，而p值大约在0.068443附近，据此分析，三个参数的初值分别选为：
               =3.0，q⁽⁰⁾=1.0，p^（0)＝0.1

将这三个初值输人程序进行运算，一次计算成功，三个参数值为：

a_g=3.382818，q=1.451636，p=0.06649397             (3-44)

将这些参数代人（3-43）式即得联轴器阻尼耗能随振幅和频率变化的函数关系式。
根据等效原理（3-34）式和S_g=W_e以及（3-44) 式可得等效粘性阻尼函数为：

将（3-44）、（3-45）式代入（3-22）式得阻尼力数学模型为

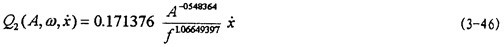
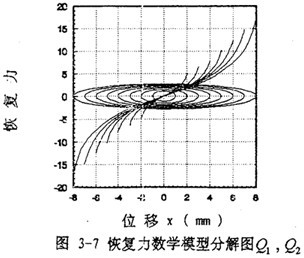
作出（3-46）式的曲线图如图3-7中椭圆所示，将图3-7中椭圆与图3-4中对应椭圆相比较可知，式（3-46）能较好地描述非线性迟滞阻尼力。

3-5关于联轴器建模与参数辨识的进一步研究
一、数学建模与参数辨识

在对前面关于联轴器建模与参数辨识工作进行思考和对联轴器试验结果进行进一步深人分析后，提出联轴器恢复力数学模型新表达式：

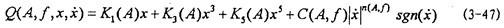
即恢复力(A,f,x， ）是振幅A、激励频率f、瞬态位移x和瞬态速度 的函数，或者说恢复力Q是刚度函数K₁（A），K₃（A），K₅（A）和阻尼函数C(A,f）以及阻尼成分函数n(A,f）的函数，其中阻尼成分函数n(A,f）描述阻尼的组成情况，n（A,f）=0时，阻尼为干摩擦阻尼，n(A,f)=1时，为粘性阻尼，0＜n（A,f)<1时，阻尼由粘性阻尼和干摩擦阻尼组成，n（A,f)>1时，阻尼成为“高阶”阻尼。对于（3-47)式，当振幅与频率一定时，式中的K_l（A），K₃（A)，K₅（A）和n（A,f）均为定数，当振幅A和频率变化时，它们均是函数，因此参数辨识实质上是参数函数的辨识。首先我们用非线性参数辨识方法Marquardt法，根据试验所得的数据，按照（3-47）式对每一迟滞回线进行参数辨识，可以得到对应的K₁（A)，K₃（A），K₅（A),C(A,f)和n（A,f）值，对每种工况下的数据随振幅和频率变化趋势进行分析后，可以建立刚度函数、阻尼函数和阻尼成份函数的数学表达式为：

然后用线性参数辨识法和非线性参数辨识法，根据上面已经得到的各个工况下K₁（A)，K₃（A），K₅（A),C(A,f)和n（A,f）的数值对（3-48）、（3-49）、（3-50）式中各参数进行辨识，将辨识得到各参数代入（3-48）、（3-49）和（3-50）式得：

关于K₅（A)的辨识采用以下方法：

当位移x达到最大值A时，联轴器恢复力Q达到最大值，弹性恢复力也达最大值，此时有：

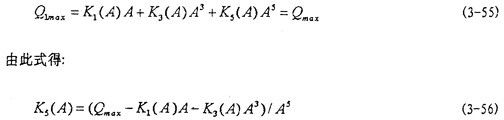
式中K₁（A)，K₃（A）已求得。由试难迟滞回线恢复力最大值与振幅的数据，可辨识出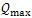（3-56）式的  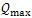                    为：

            （A）=-5.16965×10^-5A⁷+2.21538×0.0241174A⁵--0.375207A⁴+2.55596A³-8.88624A²+8.37136            （3-57）

将（3-51)、(3-52）和（3-57）式代人（3-56）即求得K₅（A)。至此，(3-47）式中的各参数函数已全部辨识出。将这些参数代入(3-47）式就得到联轴器恢复力数学模型。

二、结果分析与比较
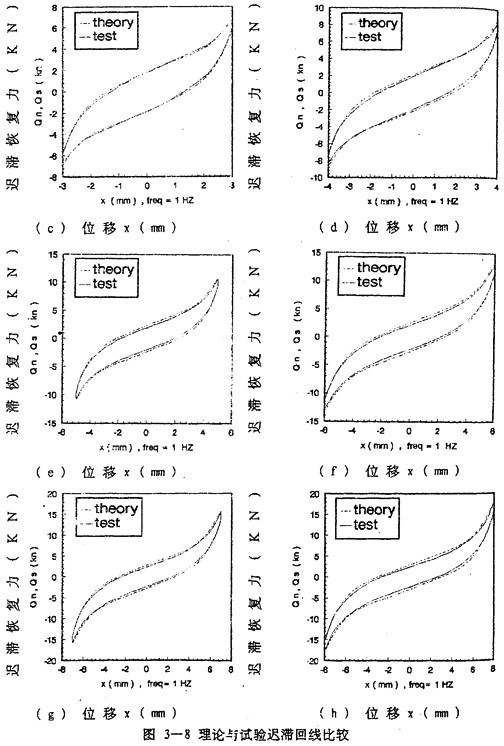
由数学模型（3-47) 计算可以得到不同激励频率和振幅下联轴器恢复力迟滞回线数据，为了证实（3-47）的正砷性，下面画出频率为1赫兹、振幅为1～8毫米各工况下数学模型计算的理论数据和试验数据表示的迟滞回线图，如图(3-8)(a）～（h)（见51～52页）所示，图中虚线为理论回线，实线为试验迟滞回线。从图中可知，理论迟滞回线十分接近试验迟滞回线，由此可以说明建立的联轴器数学模型（3-47）式可较好地描述恢复力随振幅A频率f、瞬时位移x和速度分变化的规律，较圆满地解决了联轴器恢复力建模与参数函数辨识的难题。

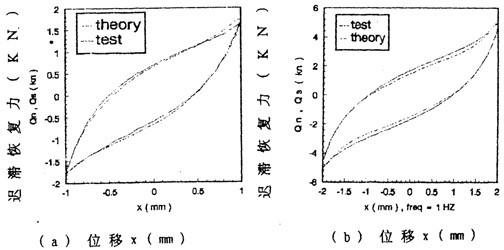
为了进一步分析联轴器的阻尼特性并与用拟合分析解法和阻尼等效原理建立的数学模型（3-12）、（3-13）、（3-14）作比较，画出由数学模型（3-47）式分别描述的弹生恢复力₁和阻尼力₂的曲线图，如图（3-9）（a）～（h）所示，图中单值曲线为弹性恢复力₁。双值闭合曲线为阻尼力₂。

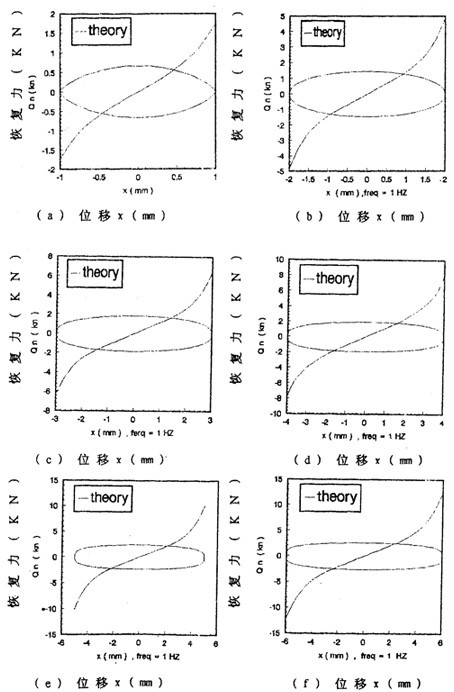
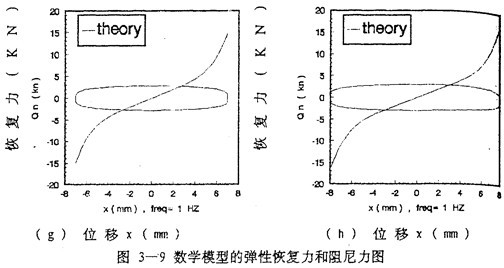
(1).从图3-9(a）-（h）中可以看到：双值闭合曲线的形状随振幅的增大，从橄榄形变成椭圆形，再变成棒槌形。说明联轴器的阻尼成分不是单一的，而是多种阻尼的组合，这些阻尼在不同的振幅下出现的大小比例不同，振幅为1毫米时，见图3-9(a）图，“高次”阻尼成分较多，而干摩擦阻尼和粘性阻尼成分较少，这时阻尼力闭合曲线的形状呈橄榄形，这是因为振幅较小时，联轴器弹性元件中的钢丝绳股与股之间所受的力和位移都较小，还没有产生相对滑移。随着弹性元件受力增加、位移增加，钢丝绳股与股之间的摩擦力增大，局部出现滑移，这种状态下，联轴器的阻尼成分以粘性阻尼为主，摩擦阻尼次之，闭合曲线，即阻尼力曲线的形状呈椭圆形，振幅为2-4毫米。见图（3-9)(b）～（d)，随着联轴器受力的进一步增大，位移随之增加，钢丝绳股与股之间出现大的相对滑移，阻尼力曲线的形状呈棒缒形，介于椭圆与矩形之间，但更加接近矩形，这说明此种情况下，联轴器的阻尼成分以干摩擦阻尼为主，粘性阻尼为次，振幅介于5-8毫米之间，见图（3-9)(e）～（h)。
(2).表3-1列出阻尼成分函数n（A,f）在1赫兹时，随振幅变化的数值，对应于图3-9中各闭合曲线。
从表中可以看出，当n（A,f)>1时，阻尼成分以“高次”阻尼为主，阻尼力曲线呈橄揽形；当0.6<n(A,f)<l时，阻尼成分以粘性阻尼为主，阻尼力曲线呈椭圆形；当0＜n（A,f)＜0.6时，阻尼成分以干摩擦为主，粘性阻尼次之，阻尼力呈棒缒形；当n(A,f)=0时，阻尼成分将变成纯粹的干摩擦，由n（A,f）的值变化可知，产生这种情况的可能性很小。由此可以知道，阻尼成分函数n(A,f)控制阻尼力曲线的形状。

（3）.从图3～9中各图可知：阻尼力的大小随振动位移x变化而变化，实质上阻尼力的大小随振动速度 的大小变化。在x等于零时，速度 最大，所以，阻尼力的绝对值达到最大，在位移x为振幅值A时，速度为零，阻尼力零。

（4）.表3-2列出阻尼函数C（A,f）在1赫兹时，随振幅变化的数值，对应于图3-9中各闭合曲线。从表中可知：随着振幅A的增大，阻尼函数随之增大，这说明了联轴器的阻尼耗能随振幅增大而增大的原因。

表3-1 阻尼成分函数n(A,f)控制阻尼力曲线的形状。

表3-2  阻尼函数C（A,f）随振幅A变化表

将数学模型（3-57）与数学模型（3-12）、（3-13）、（3-41）进行比较，可知：

（1）.数学模型（3-57）中的弹性恢复力模型中有三个刚度函数，而数学模型（3-12）中的弹性恢复力模型中有五个刚度函数，因此前者较后者简单，但精度不如后者。

（2）.数学模型（3-57）中的阻尼力中由于引入了阻尼成分函数n（A,f），因而该阻尼力模型能揭示联轴器阻尼成分的组成和变化规律；而数学模型（3-41）中的阻力模型是在阻尼等效原理的基础上建立起来的，因而不能描述联轴器中复杂的阻尼成分。由此可见数学模型（3-57）和数学模型（3-12）（3-13）（3-41）各自有自己的优点和不足，后者能较好地描述动刚度，前者能较好地描述阻尼。

（3）.数学模型（3-57）在参数辨识时，采用的方法是整体辨识法，即将联轴器的弹性恢复力和阻尼力中的各未知参数放在一起进行辨识，由于一次需辨识的参数较多。若再考虑K₇（A)，K₉（A），将使辨识难度大大增加，故在（3-57)模型中只考虑了K₁（A)，K₃（A)，K₅（A）。而数学模型（3-12）（3-13）(3一41）的参数辨识，采取的方法是拟合分解法，即将联轴器的恢复力分解成弹性恢复力和阻尼力两个式子，分别对其未知参数进行辨识。

在后面的几章中，为了计算简便些，将采用数学模型（3-12)(3-41)。
3-6小结

本章在钢丝绳弹性联轴器振动试验数据进行分析和处理的基础上，围绕联轴器的建模和参数辨识作了以下工作：

(1）在Ko等人工作的基础上，发展了一种用于非线性迟滞特性系统研究的拟合分解法。用此法将联轴器非线性恢复力迟滞回线拟合分解成两部分：非迟滞非线性弹性恢复力和纯迟滞非线性阻尼力，为分别研究非线性弹性恢复力和非线性阻尼力的特性创造条件，并将Ko法只能辨识三个阶次动刚度的方法发展为能辨识五个或更多个阶次动刚度，为描述大位移强非线性的迟滞特性提供了可行的方法。

(2）针对联轴器动刚度和阻尼是振幅和频率的非线性函数，但当频率增大到一定值后，动刚度和阻尼仅为振幅的非线性函数的特点，分别提出了不受频率影响和受频率影响的非线性弹性恢复力数学模型和非线性阻尼力模型（3-11）、(3-14）式和（3-18）、(3-21）式。根据对联轴器非线性迟滞回线随振幅和频率变化规律的分析，认为提出的数学模型能较合理和客观地描述非线性弹性恢复力和阻尼力的变化规律。
(3）研究了联轴器阻尼耗能特性，提出了阻．尼耗能仅受振幅影响和同时受振幅与频率影响的数学模型（3-38）和（3-43）式。在对联轴器非线性迟滞回线面积（即阻尼耗能）进行数值积分的基础上，经过非线性参数辨识，得出了(3-38）和（3-43）模型中的各参数。从而得到了联轴器阻尼耗能随振幅的增大而增大，随频率的增大而减小的函数关系式。
(4）以联轴器非线性阻尼耗能研究为基础，根据阻尼等效原理，研究并建立了联轴器阻尼仅受振幅影响和同时受振幅和频率影响的数学模型（3-40）和(3-45)，经过参数辨识得出了模型中的各参数，由此弄清楚了联轴器阻尼随频率和振幅变化的规律，在此基础上，建立了联轴器非线性阻尼力的数学模型（3-41）和（3-46）式。
(5）对不受频率影响的非线性弹性恢复力数学模型（3-11）式中的参数进行辨识，得出了五个动刚度函数的表达式（3-27)，分析表明，联轴器的动刚度具有刚度软化的特性，这一特性对防冲减振降噪有利。
(6）对不受频率影响的非线性阻尼力数学模型（3-14）式和受频率影响的非线性弹性恢复力数学模型（3-18）及（3-21）式进行了辨识，由于辨识算法的不合适，未能辨识出各参数，为了解决此辨识问题，有待于寻找新的和有效的辨识算法。对联轴器非线性迟滞特性的分析后，仍认为（3-14）、（3-18）和（3-21）式能合理地描述联轴器非线性弹性恢复力和阻尼力。由于频率影响范围很小，在实际计算中，用非线性弹性恢复力数学模型（3-11）、(3-27）式和非线性阻尼力数学模型（3-41）是完全可行的。
(7）对联轴器试验结果和前面关于联轴器建模与参数辨识工作进行进一步深人分析后，提出了联轴器恢复力新数学模型（3-47)，采取未知参数整体辨识法，用Marquardt非线性参数辨识方法，成功地辨识出了式（3一47）中各参数。模型（3-47）的优点是阻尼成分函数n(A,f）的引人使得它能全面地揭示联轴器中的阻尼情况。