圆柱齿轮 检验实施规范

轮齿同侧齿面的检验

1范围

本指导性技术文件是渐开线圆柱齿轮同侧齿面的检验实施规范，即齿距、齿廓、螺旋线偏差和切向综合偏差的检验实施规范。

作为标准GB/T10095.1的补充，它提供了齿轮检测方法和测量结果分析方面的建议。

许多使用的名词在GB/T10095.1中解释，其他的在它们出现的地方或在第3章中解释。

2引用标准

下列标准所包含的条文，通过在本指导性技术文件中引用而构成为本指导性技术文件的条文。本指导性技术文件出版时，所示版本均为有效。所有标准都会被修订，使用本指导性技术文件的各方应探讨使用下列标准最新版本的可能性。

GB/T 1356-2001 通用机械和重型机械用圆柱齿轮 标准基本齿条齿廓（idt ISO 53：1998）

GB/T 1357-1987 渐开线圆柱齿轮模数（neq ISO 54:1977）

GB/T2821-1992 齿轮几何要素代号（neq ISO 701:1976）

GB/T 3374-1992齿轮基本术语

GB/T 10095.1-2001 渐开线圆柱齿轮 精度 第1部分：轮齿同侧齿面偏差与径向跳动的定义和允许值（idt ISO 1328-1:1997）

GB/T 10095.2-2001渐开线圆柱齿轮 精度 第2部分：径向综合偏差与径向跳动的定义和允许值（idt ISO 1328-2:1997）

GB/Z 18620.2-2002圆柱齿轮 检验实施规范 第2部分：径向综合偏差、径向跳动、齿厚和侧隙的检验（idt ISO/TR 10064-2:1996）

GB/Z 18620.3-2002圆柱齿轮子检验实施规范 第3部分；齿轮坯、轴中心距和轴线平行度（dit ISO/TR 10064-4:1996）

GB/Z 18620.4-2002圆柱齿轮子检验实施规范 第4部分：表面结构和轮齿接触斑点的检验（idt ISO/TR 10064-4:1996）

ISO/TR 10063 圆柱齿轮 功能组、检验组、公差族（正在制订中）

3符号及相关的术语

3.1齿轮参数

3.2齿轮的偏差

单项要素测量所用的偏差符号，用小写字母（如f）加上相应的下标组成；而表示若干单项要素偏差组合的“累积”或“总”偏差所用的符号，采用大写字母（如F）加上相应的下标组成。有些偏差量需要用代数符号表示，当尺寸大于最佳值，偏差是正的；反之则负值。

fdb1)	基圆直径偏差	μm
fdbm1)	平均基圆直径偏差	μm
fe(feL，feR)	齿轮轴线和轮齿（或同侧齿面）轴心线间的偏心量	μm
ffα	齿廓形状偏差	μm
ffβ	螺旋线形状偏差	μm
fHα1)	齿廓倾斜偏差	μm
fHαm1)	平均齿廓倾斜偏差	μm
fHβ1)	螺旋线倾斜偏差	μm
fHβm1)	平均螺旋线倾斜偏差	μm
f i′	一齿切向综合偏差（与测量齿轮啮合）	μm
f l′	切向综合偏差的长周期分量	μm
f s′	切向综合偏差的短周期分量	μm
f′	一齿传动偏差（产品齿轮副）	μm
fpb1)	基圆齿距偏差	μm
fpbm1)	平均基圆齿距偏差	μm
fpbt	端面基圆齿距偏差	μm
fps1)	跨齿齿距偏差	μm
fpt1)	单个齿距偏差	μm
fwβ	波度（沿螺旋线）	μm
fα1)	压力角偏差（标准）	μm
fαm1)	平均压力角偏差	μm
fβ1)	螺旋角偏差	μm
fβm1)	平均螺旋角偏差	μm
FP	齿距累积总偏差	μm
Fpk1)	齿距累积偏差	μm
FpkS1)	跨齿k个齿距累积偏差	μm
FpS1)	跨齿齿距累积偏差	μm
Fi′	切向综合总偏差（与测量齿轮啮合）	μm
F′	传动总偏差（产品齿轮副）	μm
Fα	齿廓总偏差	μm
Fβ	螺旋线总偏差	μm

3.3齿轮检验的名词

 

1）这些偏差可以是+（正号）或-（负号）。

4齿轮的检验项目

各种轮齿要素的检验，需要多种测量操作。首先，必须保证在所有测量中如涉及齿轮旋转时，齿轮实际工作的轴线应与测量过程中旋转轴线相重合。

在检验中，既不经济也没有必要测量全部轮齿要素的偏差，如单个齿距、齿距累积、齿廓、螺旋线、切向和径向综合偏差、径向跳动、表面粗糙度等，因为其中有些要素对于特定齿轮的功能并没有明显的影响。另外，有些测量项目可以代替别的一些项目，例如切向综合偏差检验能代替齿距偏差检验，径向综合偏差检验能代替径向跳动检验。由于考虑到有这类情况，在ISO/TR10063中按齿轮工作性能推荐了检验组和公差族。然而，应该强调，对于质量控制测量项目的减少，必须由采购方与供方协商确定。

5偏差位置的识别

结合轮齿的测量，识别偏差的方便办法是阐明其涉及的位置，如右齿面、左齿面、齿距或它们的成组。

5.1右或左齿面数

选定齿轮的一面作基准面，并标上字母“Ⅰ”，另一个非基准面为“Ⅱ”

对着基准面进行观察，看到齿和齿顶，则右齿面在右边，左齿面在左边（见图1、图2）。

右和左齿面分别用字母“R”和“L”表示。

 

 

 

图2内齿轮的标记和编号

5.2斜齿轮的右旋或左旋

外齿或内齿斜齿轮的螺旋方向，由右旋或左旋表示，螺旋方向分别由字母“r”和“l”表示。当齿轮轴竖立于观察者前方，所见轮齿向右（左）上方倾斜者为右（左）旋齿轮。

5.3齿与齿面的编号

对着齿轮的基准面看，以顺时针方向顺序地数齿数，齿数后写上字母R或L，表示它是右或左齿面，比如“齿面29L”。

5.4齿距的编号

单个齿距的编号和下个齿的编号有关，第N齿距介于“N-1”齿和第“N”齿的同侧齿面之间，用字母R或L表示齿距是介于右齿面还是左齿面之间，例如“齿面2L”（见图1）。

5.5齿距数“k”

偏差符号的下标“k”表示所要测量偏差的相邻齿距的个数，实践中，数字往往取代k，比如F_P3表示3个齿距的齿距累积偏差。

5.6检验的规定

通常，测量应在邻近齿高的中部和（或）齿宽的中部进行，如果齿宽大于250mm，则应增加两个齿廓测量部位，即在距齿宽每侧约15%的齿宽处测量，齿廓和螺旋线偏差应至少在3个以上均布的位置同侧的齿面上测量。

6单个齿距和齿距累积偏差的检验

6.1概述

齿距偏差的检验包括测量其实际值（角度值）或者沿齿轮圆周上同侧齿面间距离作比较测量（见图3）。

与检验法向、端面和齿轮累积偏差不同，基圆齿距偏差是在沿基圆切平面上测量，因而与齿轮轴线无关。

图3齿距（p_t），齿距偏差（f_pt）

表1为单个齿距测量虚拟偏差数据处理举例表，表中的整数值实际上是很难遇到的。表中：N=齿距序数；A=用二测头测得的相对齿距偏差值；B=所有A值的算术平均值；C=单个齿距偏差f_pt，表示为A与B的差值；D=由f_pt(C)值依次连续累加而得的齿距累积偏差。表1涉及到第18和第1齿之间的各齿面，其说明见图4。

一般地，对于有很多齿数的齿轮，F_P和F_PS的差别可忽略不计。

表1单个齿距测量数据

当用角度齿距测量方法时（即用一个触头的仪器），在每个测量位置上，将实际测得的角度减去理论角度，再将此差值（弧度）乘以触头与齿面接触点的径向距离，即可得到D值。而C值则可由N号的齿面的D值减去N-1号齿面的D值获得。

图4 表1示例的齿轮（z=18）的齿距偏差的图解说明

6.2单个齿距精度的检测

检测齿距精度最常用的装置，一种是有两个触头的齿距比较仪，另一种是只有一个测量触头的角度分度仪，对实施这两种检测方法分别在6.2.1和6.2.2中阐述。

不带旋转工作台的坐标测量机也可用来测量齿距和齿距偏差，所采用的有关相对运动与6.2.2中所述的原理基本相符（见图5）。

图5 端面齿距p_t和单个齿距偏差f_pt

6.2.1用齿距比较仪（两个触头）检测单个齿距

  两个测头的位置，应在相对于齿轮轴线的同样半径上，并在同一横截面内，测头移动的方向要与测量圆相切。

因为很难得到半径距离的精确数值，所以齿距比较仪很少用于检测端面齿距的直实的数值。这种仪器最合适的是用途是确定齿距偏差。

 一些齿距比较仪器装备了导向滑轨，使测头容易达到固定的径向深度，一般到轮齿中部的附近（图6），被检的齿轮慢慢地转动，绕着轴心连续地或间歇地转动，而导向滑轨上的测头在测量部位来回移动。

图6使用齿距比较仪测量齿距偏差

6.2.2用角度转位法（一个触头）检测单个齿距

检测过程涉及分度转位器的使用，其精确度必须和齿轮直径相协调，如图7所示。

对每个齿面，测量头在预先设定要检测的部位上径向来回移动，就可测得偏离理论位置的位置偏差，相对于所选定的基准齿面或零齿面，这个测得的数据代表了相差齿面的位置偏差，这样记录的数据曲线应显示出齿轮在圆周上的齿距累积偏差（F_pk）。

第N个齿面的位置偏差减去第N-1个的，就是每个单个齿距偏差，负值要表示出来。

图7 用角度法转位法检验齿距

6.3用齿距比较仪检测法向齿距精度

图8表示法向齿距和法向齿距偏差f_pn。

 

图8法向齿距P_n和法向齿距偏差f_pn（法向截面）

检测时，当只有检验“法向”齿距偏差的便携式比较仪，而没有其他适当的仪器时，只得用法向齿距偏差测量来代替端面齿距偏差的测量。如图9介绍的仪器，齿轮的齿顶圆用来定位，它必须和齿轮轴线有足够的同心度，其他用于同样用途的比较仪器有不同的定位方法，而不用齿顶面作为定位面。

图9在直齿轮上用于检测法向齿距偏差的便携式齿距比较仪

因为标准GB/T10095.1中的公差值指的是端面齿距，所以在和公差比较前，法向齿距偏差测量值需转换为端面数值。

它们的关系如下：

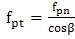
………………（1）

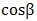
或者，可将公差值乘以 ，这样做所需的计算量往往比较少。

法向齿距偏差测量值不能加起来作齿距累积偏差。

6.4基圆齿距p_b和基圆齿距偏差f_pb的测量

一个齿轮的端面基圆齿距是公法线上的两个相邻同侧齿面的端面齿廓间的距离，它也就是位于相邻的同侧齿面上渐开线齿廓起点之间的基圆圆周上的弧长度（见图10）。

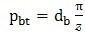
…………………………（2）

图10端面基圆齿距p_bt

法向与端面基圆齿距之间有如下关系：

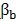
p_bn=p_btcos ………………（3）

相啮合的齿轮各齿之间有效负荷的分配，要求两个齿轮的基圆齿距精度能得到充分的控制，在两个齿轮要求能互换时，这点就显得尤其重要。这种情况下，一个重要的测量目标，就是确定用于与其他齿轮的平均基圆齿距相比较的该个齿轮的平均基圆齿距。

法向基圆齿距的理论值是法向模数和法向压力角的函数，即：

p_bn=mπcosα_n………………（4）

通常，我们用便携式比较仪来测量法向基圆齿距偏差，这种仪器的使用原理如图11所示，借助于一组合适的量规，基圆齿距比较仪在标定后也能直接用来测量与理论基圆齿距的偏差。

图11测量基圆齿距的便携式比较仪测直齿轮

在测量基圆齿距时，必需保证比较仪的触头的接触点不在齿廓或螺旋线的修形区域内。

当手头没有合适的齿廓检查仪器时，测得的基圆齿距偏差可用作推断压力角偏差f_α的基础，因为测得的基圆齿距偏差受到齿距偏差和齿廓形状偏差的影响，这步骤只能在后面两种偏差很小时才能使用。

在计算近似的平均压力角偏差或其他偏差时，应该用基圆齿距的平均值。

平均法向基圆齿距偏差f_pbm，平均基圆直径偏差f_dbm、平均压力角偏差f_αm和有效基圆直径d_beff有以下关系：

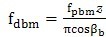
……………………（5）

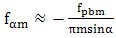
………………（6）

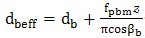
………………（7）

6.5齿距累积偏差F_pk和F_P的确定

齿距累积偏差是这样确定的，即对任何指定数目的端面单个齿距偏差（见图4b）作代数相加，单个齿距偏差的测定见6.2.1。

用6.2.2阐述角度转位法可直接测得齿距累积偏差值。

6.5.1齿距累积总偏差F_P的确定

按照定义，齿距累积总偏差是指一个齿轮的任意扇形部分同侧齿面间的最大齿距累积偏差，其数值等于齿距累积偏差曲线的最高和最低点之间的距离，见图4b。

6.5.2齿距累积偏差跨齿距检测

当齿轮的齿数很多用比较仪作单个齿距校验法测量时，由于很多个测量的不正确性叠加起来而形成很大的误差，每次测量中不正确性的来源之一，是很难保证后触头与前一次测量时前触头所占位置完全重合。

如果用跨齿距进行检验，则上述的不正确性可以减少，为此建议当齿轮超过60个齿时，最好改用跨齿距测量，图12表示跨齿距数为4的测量原理，即齿距号1至4，下一个要测的扇形区包含齿距号5至8，此时位于右侧的后触头将与4号齿齿面接触，此接触点应为上一次测量时位于左侧的前触头所占的位置，6.2.1所述的注意要点同样适用于跨齿距测量。

图12跨齿距测量原理

在选择跨齿数（每跨齿距数）S时，必须符合以下两点：

a)       每跨的弦长应适合所用的齿距比较仪的量程；

b)       测得的点数应足够用来绘制出一条可接受的累积偏差的曲线。

图13中所提供的公式和曲线可指导选择合适的齿距数。

如果可能，z/S应取整数，但是，如z/S不是整数时，跨齿距偏差测量的跨齿数应取大于z/S的整数，此时当测量到量后一个跨齿距时，其中包含的一部分齿距是在第一个跨齿距测量时已经包含了的。

   例：z=239，m=8,这样S=5

故跨数（读数个数）至少等于239：5=47.8，取跨数（读数个数）为48个，则测量重叠的齿距为5×48-239=1（齿距）。

图13跨齿距测量时每跨齿距数（S）的选择

6.5.3跨齿距测量结果的评定

跨齿距偏差的代数和建立起来的曲线，常常不能反映齿距累积总偏差，认识这一点是很重要的，因为跨距内最极端的单个齿距偏差的影响，原来会影响齿距累积总偏差的数值，但却在跨距内被抵销了。

这样，如果任何一个数值非常接近于给定的公差极限，则最小、最大和重叠区内的单个齿距偏差应该融入跨齿距累积偏差曲线中，以保证齿距累积总偏差更加精确。

用数字取代符号F_ps和F_PKS的下标，表示跨齿距累积偏差可带来很大方便，用这种方法，就可以表示出有关的弧长或齿距数，例如，F_P24S4表示在S=4（跨距数）跨齿测量下，k=24齿距弧长内的跨齿距累积偏差。

6.5.4齿距累积偏差F_PK的必要性

如果在较少的齿距数上的齿距累积偏差过大时，在实际工作中将产生很大的加速度力，这在高速齿轮传动中更应重视，因为可能产生很大的动载荷，因而有必要规定较少齿距范围内的累积公差。

图14中分别表示了两个齿轮的齿距累积偏差曲线，从两曲线中可看出其齿距累积总偏差是一样的，但少数齿距的最大齿距累积偏差有着明显的差别，如曲线a和b中k个齿距所示，按照规定的公差值，曲线a中的F_P4的偏差是可以通过的，而在曲线b中F_P4的偏差是不能接受的。

给定数目的k个齿距上的最大齿距累积偏差F_pk可由F_pk图导出，即依次从齿轮的每个齿面出发取圆弧长度（k×p_t），实际上其最大值也可在少数跨齿距测量中得到。

现看图4例子上提供的数据，当k=3，第15，16和17齿距的单个齿距偏差的总和，表明了三个齿距最大齿距累积偏差为10μm。

区别F_pk值的位置的一个简便方法是，在圆括号中列出有关的齿距序数，例如，上面的例子可按下列表示：

F_P3（15…17）=10μm

6.6关于齿距偏差测量和对其结果评价的一些说明

单测杆和比较仪测杆末端通常是球形，每个测杆轴心线应与从齿轮轴心线到测杆和齿面接触点这一径向线平行（图6、图7和图12）。

对于所有齿距偏差的测量方法，除了用基圆齿距比较仪测量基圆齿距偏差外，其径向和轴向跳动的值都应很小，以至可以忽略不计。然而，如果待检齿轮的轴心线偏离检测仪器回转的轴心线，而计量装置的位置又按后者的轴心线固定时，则双倍振幅等于两倍偏心量的正弦分量，要加入到齿轮齿距累积偏差的真实曲线上去。

由于上面提到的偏离（偏心量f_e）所形成的正弦曲线，构成齿距累积偏差图（图14a）的一部分，是从仅仅一组同侧齿面得到的，其相位将不同于由左侧和右侧齿面综合得到的径向跳动曲线，它的双倍波幅等于2f_e,波幅也可能不同。

图14齿距累积偏差曲线图

由齿轮累积偏差值或切向综合偏差值的测量得到偏心量的数值，涉及右侧或左侧齿面的，最好用f_eR或f_eL分别表示。

7齿廓偏差的检验

按定义，齿廓偏差是在端平面上垂直于齿廓的偏差值，然而，偏差也可在齿面的法向测量，然后把测得的数值除以cosβ_b，经这样的换算后再与公差值比较。

7.1齿廓图

齿廓图包括齿廓迹线，它是由齿轮齿廓检验设备在纸上或其他适当的介质上画出来的齿廓偏差曲线，齿廓迹线如偏离了直线，其偏离量即表示与被检齿轮的基圆所展成的渐开线齿廓的偏差。

齿廓修形也表现为偏离了渐开线，但就“设计齿廓”而言这种情况下不能作为偏差来对待。

沿齿廓图上任何一点，均可与一个半径、一个基圆切线长度和一个渐开线滚动展开角相联系。

图15是一个齿廓的示例以及其与相应齿廓迹线的关系和有关的术语。关于齿廓迹线术语的详细定义和概念在GB/T10095.1中叙述。

齿廓计值范围L_α等于在有效长度L_AE中从其顶端或倒棱处减去8%，这样做是为了在评定时排除在切削过程中非有意的多切掉的顶部，而这样做并不损害齿轮的功能，在评价齿廓总偏差（F_α）和齿廓形状偏差（f_fα）时，在这8%区域内如有超出设计齿廓的材料，从而增加其偏差量时必须计算进去，而在这区域内如多切去材料而形成的偏差值，其公差可予增大。

7.2齿廓图的评定

为了齿轮质量分等，只须检验齿廓总偏差F_α即可，见GB/T10095.1。

然而，为了某些目的，分别确定“齿廓倾斜偏差”f_Hα和“齿廓形状偏差”f_fα也是有用处的。为此，需要在齿廓图上加上“平均齿廓迹线”如图15所示，参见GB/T10095.1-2001中图2a、b、c。关于f_fα和f_Hα允许值，作为指导性资料在GB/T10095.1-2001附录B中给出。

图15齿轮齿廓和齿廓示意图

从齿面法向上测得齿廓偏差，如果检测仪器未转换成端面值时，则其结果应除以cosβ_b转换为端面齿廓法线上的相应值，然后将获得的数据同端面齿廓法向偏差的规定公差值比较。

7.3f_Hα和f_α的代数符号

如图15所示，在图形中平均齿廓迹线若向齿顶A侧升高，则齿廓倾斜偏差称为正，则相应的压力角偏差称为负。在图16中表示了由于安装于齿轮加工机床上有偏心而造成的正倾斜及负倾斜。

如一对相啮合齿轮，其齿廓图中的倾斜相等并且符号相同，则其偏差就相互抵销，这一规律对外齿轮和内齿轮都适用。

7.4压力角偏差f_α

齿廓线如在齿顶端凸出，表示其压力角减小。

图16平均齿廓倾斜偏差f_Hαm

齿廓倾斜偏差可按下列公式换算为压力角偏差f_α

按弧度

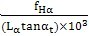
f_α=- ………………（8）

按角秒

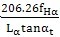
f_α=- ………………（9）

式中：f_Hα单位为μm，L_α单位为mm。

对于外齿轮、内齿轮：

当f_Hα＞0,见f_db＞0 f_α＜0。

7.5平均齿廓倾斜偏差

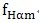
单个齿廓的倾斜偏差可能是由于制造或检验时安装不准确形成的偏心所造成，但是，这种偏差沿着齿轮圆周是变化的，对于同侧齿面的平均齿廓倾斜偏差，这种变化就相互抵销掉了。

图16中，举例表示了偏心对齿廓倾斜的影响，以及平均齿廓偏差的确定。

往往需要计算出同侧齿面齿廓倾斜偏差的平均值，以用来确定应采取什么步骤来纠正机床上装夹时产生的误差。

在实际应用中，取沿齿轮圆均布的几个同侧齿面计算其齿廓倾斜偏差算术平均值即可。

取两个在直径上相对位置的同侧齿面，从其齿廓迹线上可以得到适用的平均值，然而，如齿廓倾斜偏差沿齿轮圆周变化时，则必须至少取三个均布同侧齿面的齿廓线，否则偏差不一定能被发现。

7.6基圆直径偏差f_db、平均基圆直径偏差f_dbm和有效基圆直径d_beff

基圆直径偏差f_db=d_eff-d_b直接与齿廓倾斜面偏差f_Hα有关，其关系式如下：

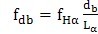
………………（10）

这样，当“平均齿廓倾斜偏差”（见7.5）确定之后，平均基圆直径偏差和有效基圆直径可按下列公式计算：

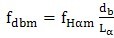
………………（11）

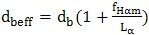
………………（12）

7.7齿廓公差带

一个方便的检验方法是检验齿廓迹线是否位于规定的公差带之内。

很多公差带的规定，其形状大体上像字母“K”（图17），即众所周知的“K”形图。

图17用公差带法检验齿廓精度

这种图的应用如图17所示，其中图17a所示齿廓迹线落在公差带之内，而在图17b中则没有达到。

如果需要的话，也可综合应用两种齿廓精度评定方法（即用某一质量等级的标准公差和用公差带法），如图18中的例子所示。

图18 不同齿廓区段用不同公差实例

7.8齿廓凸度C_α

在有些应用中，适当的齿廓修形涉及顶部和根部，修削使轮齿从中间开始逐渐向顶部和根部形成弓形，如图19所示。

图19齿廓凸度C_α

渐开线曲率增加的高度可用下面方法确定

在线图中，用一条直线将齿廓迹线与计值范围（L_α）两端交点连起来，如图20所示，在这条直线与另一条和它平行且相切于平均曲线间的距离（在记录偏差的方向测量），就等于该齿廓的凸度（C_α）。

有意做成的凸形齿所产生的齿廓线图，其设计齿廓和平均齿廓迹线通常为呈抛物线。

图20齿廓凸度C_α的确定

8螺旋线偏差的检验

按定义，螺旋线偏差是在端面基圆切线方向测量的实际螺旋线与设计螺旋线之间的差值，如果偏差是在齿面的法向测量，则应除以cosβ_b换算成端面的偏差量，然后才能与公差值比较。

8.1螺旋线图

螺旋线图包括螺旋线迹线，它是由螺旋线检验设备在纸上或其他适当的介质上画出来的曲线，此曲线如偏离了直线，其偏离量即表示产际的螺旋线与不修形螺旋线的偏差。

设计者所采用的螺旋线修形，也表现为同直线的偏离，但这种情况不能作为“设计螺旋线”的偏差来对待。见GB/T10095.1-2001中3.3.1.3。

有时用放大迹线长度来表较小齿宽，或缩小表示较大的齿宽。“迹线长度”见GB/T 10095.1-2001中3.3.1.1。

关于右和左螺旋线，可分别用字母“r”、“l”作为标或下标。

在图21一个曲型的螺旋线图例中，可看到设计螺旋线未修形时齿面的螺旋线偏差，如果“设计螺旋线”是鼓形，齿端减薄或别修形时，则其迹线奕为适当形状的曲线。

图21螺旋线图示例

有关螺旋线迹线的详细术语、定义和概念，已在GB/T10095.1中叙述。

螺旋线计值范围L_β等于迹线长度两端各减去5%的迹线长度，但减去量不超过1个模数（1m），所以要提出此减去量是为了有些机加工的条件所引起的，非有意的少量端部减薄不计入偏差量的评定中去，在评定螺旋线总偏差（F_β）和螺旋线形状偏差（f_fβ）时，若在5%区域内有多余的材料，则增加的偏差必须考虑时去，而在这区域内如多切去金属而形成的偏差值，其公差可予增大。

8.2螺旋线图的评定

对于齿轮质量分等只需检验“螺旋线总偏差”F_β即可，见GB/T 100095.1。

然而，为了某些目的，分别确定“螺旋线倾斜偏差”f_Hβ和“螺旋线形状偏差”f_fβ也是有用处的，为此，需要在螺旋线图上加上“平均螺旋线迹线”如图21。关于 f_fβ和f_Hβ公差值，作为指导性资料在GB/T10095.1-2001附录B中给出。

从齿面法向上测得螺旋线偏差，如果未由检测仪器转换成端面值时，则其结果应除以cosβ_b转换为端面齿廓法线上的相应值，如此所得值可以作为端面齿廓法向计量的偏差与给定的公差比较。

8.3用检测轴向齿距来确定螺旋倾斜偏差。

如不可能得到螺旋线图时，例如很大的齿轮不可能在测量机上测量时，则用轴向齿距仪的量值来确定“螺旋线倾斜偏差”f_Hβ。

这类仪器主要包括一个精密的水准仪和两个球形针头，两个球的间距要要调整到近似为轴向齿距的整数倍，两个球放入轮齿齿槽间，使其连心线大致与齿轮轴线平行，然后调整水准仪到零点，记录下沿齿轮其他位置上偏离零的相对斜度，这样确定的斜度，连同针头间的距离，可以用来计算出齿面的平均螺旋线倾斜偏差，这个方法的测量精度是不太高的。

如果这种测量是在齿轮圆周三个以上均无的位置时行的，此时端面齿距偏差对测量结果的影响趋于抵销，，从而可以计算出与齿轮轴线无关的近似平均“螺旋线倾斜偏差”。

另外，只要所有齿面没有严重的齿廓偏差，也没有修成鼓形，则左侧和右侧齿面的平均“螺旋线倾斜偏差”都可确定。

这种测量方法不论齿轮处于什么姿态都是有效的。

应用这种方法必要的条件是：齿宽必须大于一个轴向齿距。

8.4f_Hβ和f_β的代数符号

螺旋线倾斜偏差f_Hβ和螺旋角偏差f_β应有一个代数符号，使之完整。

当螺旋角较设计的螺旋角大时，偏差为正（f_Hβ＞0和f_β＞0），反之较设计的螺旋角小时，则偏差为负。

直齿圆柱齿轮的螺旋线偏差如果不等于零，则不用代数符号表示，而改用注脚“r”和“l”表示，即分别代表右旋或左旋的偏差。

如果一个齿轮与基相啮合的齿轮，其齿面的螺旋线倾斜偏差f_Hβ和f_β大小相等，代数符号一致，则其偏差是相互抵消的。

8.5平均螺旋线倾斜偏差f_Hβm和平均螺旋角偏差f_βm。

如果在加工一个齿轮时，齿轮的轴线偏离了切齿机床的轴线或两轴线相交，则该齿轮轮齿的螺旋线倾斜偏差沿着齿轮的圆周是变化的，见图22.

图22有偏心或倾斜的齿轮圆周上四个均布齿面的螺旋线倾斜偏差的迹线

即使其偏差是在规定的公差范围内，也必须注意这种缺陷有可能引起齿轮在工作时产生振动，因而要采取措施以避免再出现此种情况。

为了纠正加工机床上的安装或为了与相啮齿轮相匹配，需根据在齿轮圆周三个以上均布齿面所测得的若干个偏差来计算其平均螺旋线倾斜偏差。

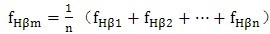
………………（13）

取在直径上对置的同侧位置的齿面，从其螺旋线图上可以获得适用的平均值，然而，如螺旋线倾斜偏差沿齿轮圆周变化时，则必须至少取三个均布齿面的迹线。否则其偏差不一定能被发现。

8.6螺旋线公差带

检测螺旋线精度的一个简便方法，是看迹线是否在给定公差带内。

这个方法实质上和“齿廓公差带”是同样的（见7.7）。

8.7轮齿的鼓度C_β

在线图中，未修整齿面的螺旋线迹线是用一条直线来表示，而鼓形齿的齿面其相应的迹线是弓形曲线，在线图中，鼓形齿齿面的设计螺旋线和平均螺旋线变线通常是抛物线（见图23）。

  轮齿鼓度C_β的评定步骤，与7.8中阐述的齿廓凸度C_α是类似的。

图23轮齿的鼓度C_β

8.8波度

   波度是螺旋线形状偏差，具有不变的波长和基本不变的高度，切齿机床传动链元件的偏摆是导致出现波度通常的主要原因，特别是：

a)  刀架进给丝杠的偏摆；

b)  分度蜗轮传动中蜗杆的偏摆。

由于原因a）所造成的波度的波长，在沿螺旋线方向测量时，等于进给丝杠的螺距除以cosβ。

由于原因b)所造成的波度，其波长为：

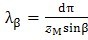
………………（14）

由于原因b)所造成的波度，其波数（投影到端面上计数）等于主分度蜗轮的齿数Z_M。这可能造成在噪声谱中那部分刺耳的单纯音，其频率相当于被测齿轮的旋转速度（转数）乘以Z_M。

图24说明了在螺旋线检测仪器上装置波度测量附件的应用方法，这将在下面讨论。

在检测原因a)或b)造成的波度曲线时，计算出相关的波长，把附件的球形定位脚放在奇数个波长的间距上，随后使定位脚沿螺旋线滑动，波度的数值由位于定位脚中间的测头显示出来。

图24波度曲线检测原理

图24中可看到，当测头接触波峰而后又接触波谷时，就如图显示的那样，测头的位移等于两倍波高，这个特点提高了仪器的灵敏度，测量结果以图的形式绘制出来。

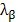
需要注意的是，若定位脚的间距为偶数个波长时（图24，s=4 ）,波度就显示不出来了。

9切向综合偏差的检验

9.1概述

为进行切向综合偏差的检测，两个齿轮其中一个可以是测量齿轮，以适当的中心距相啮合并旋转，在只有一组同侧齿面相接触的情况下使之旋转直到获得一整圈的偏差曲线图。

作为切向综合偏差检测时，需施加很轻的负载和很低的角速度，以保证齿面间的接触所产生的记录曲线，反映出一对齿轮轮齿要素偏差的综合影响（即齿廓、螺旋线和齿距）。

下列几种组合都可用于检测：

a)  一个产品齿轮和一个测量齿轮；

b)  一对相配的产品齿轮；

c)  两个以上齿轮相啮合的齿轮轮系。

关于a）种情况，以产品齿轮转一周后，即产生适用的记录，但必须注意，测量齿轮的精度将影响检测的结果，如测量齿轮的精度比被检验的产品齿轮的精度至少高4级时，则测量齿轮的不精确性可忽略不计，但如果测量齿轮的质量达不到比被检齿轮高4个等级时，则测量齿轮的不精确性必须考虑进去。

切向综合总偏差（F_i′）是指一个齿距位移间的切向综合偏差。

关于b）种情况，涉及两个产品齿轮所产生的偏差（F′和f′），称为“齿轮副的传动偏差”。为了完全确定完整的偏差谱图，必须继续旋转，直至两个产品齿轮的旋转数分别等于另一相配齿轮齿数被齿轮副两个齿数的最大公因数除所得的数，用这种方法确定的旋转数符合齿轮副的完整啮合周期。形成的偏差曲线图反映出齿轮副中两个齿轮的轮齿要素的各分量，如果要检测出单个齿轮的轮齿偏差，必须对数据作适当的处理（见9.3.3.2）。

如果有适当的试验台，重载齿轮的切向综合偏差也可用类似方法检验，但在这种情况下，记录下来的偏差受到轮齿受载变形，啮合刚度变化以及由于旋转速度面产生冲击和轮齿的几何形状不完善等因素的影响，故GB/T10095.1不适用于这类检测。

关于c）是齿轮传动运动学的评定，这种检测不属于GB/T10095的应用范围。

9.2产品齿轮与测量齿轮副的检测

9.2.1直齿圆柱齿轮

切向综合偏差的记录图，包括齿轮和测量齿轮啮合作完整圈旋转数的长周期成分，和加在其上的各齿相继啮合的短周期成分。

图25是切向综合偏差的记录曲线，它是在与测量齿轮啮合时，16个齿的产品齿轮转一转所形成的。

图25 直齿圆柱齿轮切向综合偏差图

9.2.1.1直齿轮齿廓偏差的影响

在切向综合偏差检测中，如果所用的测量齿轮是完全精确的，这就意味着切向综合偏差图上所表示的只是产品齿轮的轮齿各要素的偏差的综合。

图26所示意的是相当于三种不同齿廓的产品齿轮与测量齿轮相啮合产生的三个齿啮合周期的切向综合偏差记录图，第一个表示无修形也无误差，第二个则表示自齿高中部开始到有效齿廓两端逐渐修形，而第三个则表示有“倾斜偏差”。

图26直齿轮齿廓偏差的影响

图25中注明了切向综合总偏差F_i′，最大一齿切向综合偏差f_i′以及齿廓分量“a”和单个齿距成分“b”。

图26A表示为被测齿轮和测量齿轮两者均为无误差、无修形的齿轮时，得到一条直线形图。

图26B中，记录图表示齿顶和齿根修削，形成整个齿廓为凸形（C_α）从被动产品齿轮的齿顶开始进入啮合时起，偏差值逐渐增加到零，即接近齿高中部时，然后是逐渐减少的趋势，一直到轮齿啮合结束。

图26C中，图中所示三角形的成分，表示产品齿轮的接触由齿顶逐渐移到有效齿廓起点时，切向综合偏差逐渐从零变为一个负值，在这一点时，接触突然转移到下一个齿，从而产生一个突变为正的各齿相等的切向综合偏差。

必须记信：记录下来的切向综合偏差线图并不仅反映检验少数几数几个齿的齿廓偏差的影响，而且受到产品齿轮轮齿工作齿面上任何凸出物接触的影响。

9.2.1.2直齿轮齿距偏差的影响。

如果在齿距N处产生一个齿距偏差，是当旋转接触过程从N-1齿转移到N齿时，一个局部的切向分量将显示在切向综合偏差图上，它表现为图上齿廓展成分量中一个分量的位移。

图27表示单个齿距偏差对切向综合偏差的影响。

图27直齿轮单个齿距偏差的影响

当各齿通过啮合时，单个齿距偏差在切向综合位移圆弧上有累积作用。这种影响在切向综合偏差图上看得很清楚，这样，可确定齿距累积偏差值，（比如k=2.3,…）即在适当数量的齿距间测顶点切线的纵坐标。图28中表示了单个齿距偏差、单个齿距和齿廓组合偏差以及近似的齿距累积总偏差。

图28直齿轮的切向综合偏差及其各成分

9.2.1.3直齿轮螺旋线偏差的影响

螺旋线偏差其大小和符号对一个齿轮的每一个齿都一样时，意味着相啮合时有一致的局部接触区，因此，切向综合偏差不会受什么影响。

如果沿一个产品齿轮一圈上各齿的螺旋线偏差的大小和符号均改变时，则切向综合偏差将受到影响，螺旋线偏差大小的改变将影响切向综合偏差。

如果在这种情况下，啮合相对的两端点的齿廓偏差也不相同，则切向综合偏差图上的齿廓（一齿综合）成分也将受到影响。

9.2.1.4直齿轮重合度的影响

由一对“测量齿轮与产品齿轮”啮合所得出的切向综合偏差图，是由代表大部分齿廓偏差的一系列相继的曲线组成的，如图29所示。在齿轮进入啮合到脱开的整个周期中，切向综合偏差与“两对齿一单对齿一两对齿”啮合段的相位间的关系，在图中已清楚地表明，很容易看了：当重合度ε_α等于1时，可实现最长的单对齿啮合线，随着重合度的增加，单对齿啮合长度就相应减小，而当重合度等于或大于2时单对齿啮合段就不存在了。

为了获得尽可能多的有用数据，测量齿轮的轮齿高应做得尽可能地深（在有足够齿顶宽的条件下），这样一来，就可以在加大中心距的情况下进行检测，使其重合度为1；还可以进行这样检测，将中心距调整到使其实际运行的工作齿面都能显示出来。

图29（直齿轮）切向综合偏差图上齿间接触转移对齿廓分量的影响

9.2.2斜齿轮

当总重合度ε_γ小于2时，斜齿轮的啮合情况与重合度ε_α小于2的直齿轮是相类似的，在这情况下，上面关于直齿轮的说明对斜齿轮同样适用。

在通常情况下，斜齿轮的总重合度ε_γ常常超过2，这时，表示齿廓偏差的短周期成分将变得到某种程度平滑，这是由于有两对以上的齿同时啮合之故。

图30所示线图中，情况“A”为斜齿轮而“B”则为直齿轮，显示出两种情况下重叠齿影响的差别。

当评定切向综合偏差检测的结果时，必须十分小心，这是因为这种测试的结果，可能与考虑理论重合度及假定斜齿轮的齿廓和齿宽上均是理想的接触时所获得的结果大不一样。

在满负载时，工作齿面上的接触斑点即使是均匀分布的，在轻载下进行切向综合偏差检测时，就不见得是这种情况了，此时齿面上接触斑点也可能是局部的。这情况说明，检测时的重合度比理论计算的要小的多。

图30重合度的影响

9.3应用举例

9.3.1缺陷的识别和定位

切向综合偏差的检测，可帮助我们方便地辨认影响传动质量的偏差并找到其部位。例如从图31很容易看出一个轮齿有缺陷。而且往往有可能就地作出纠正措施。在这种情况下，调整的效果可以很快得到验证。

图31部分的切向综合偏差图实例解释

9.3.2齿轮的选配啮合

在一些特定的情况下，两相配齿轮的齿数相等可成整倍数，而且不要求互换时，可采用特殊的步骤以实现最优的工作性能。得到最优啮合效果的办法是：将齿轮转动一个90°的相位使之重新啮合，以便初步找到哪个象限时其切向综合偏差为最小。在此基础上，再将齿轮的相位转动一个比90°小的角度，最后找出最优的啮合相位。

在图32中表示出一对齿轮（左侧和右侧）在不同相位啮合时的线图。

从图中可以很明显地看到左齿面和右齿面的切向综合偏差图是不一样的。因此，对一个双向转动都要求高传动精度的齿轮副，要选择一个中间的啮合相位，以获得最佳的折衷效果。

图32啮合相位改变对切向综合偏差图的影响

9.3.3切向综合偏差数据的识别分析

9.2提代了切向综合偏差图的数据识别的资料，当用一个测量齿轮形成切向综合偏差图时，产品齿轮只需旋转一圈。如果两个产品齿轮啮合，就需旋转若干圈来形成足够的切向综合偏差图。

使用仪器处理数据，可分离和记录切向综合治理合偏差的长周期和短周期成分，可使重要数值识别和定位相对地容易。

重要的事是记住，在滤掉长周期分量后，一齿切向综合偏差f_i′(图33A)实际上变小了，这样真正的最大偏差f_i′就未必能在经滤波后的短同期分量的曲线（图33C）中表示出来。

9.3.3.1产品齿轮与测量齿轮测试数据的分析

从一幅完整的切向综合偏差线图中，可以很方便地识别出切向综合总偏差F_i′和最大一齿切向综合偏差f_i′。但是，为了辨认出长周期成分f_i′的最大值和重要的短周期分量f_s′，需要用一个滤波系统来处理数据信号，经低通滤波得出长周期分量，而经高通滤波得出短周期分量。

图33A表示未滤波的切向综合偏差信号，图33B和33C分别表示经上述处理后的长周期和短周期分量。

9.3.3.2产品齿轮副测试数据分析

产品齿轮副啮合所形成的切向综合偏差线图，通常显示出一系列的周期性偏差，相应于逐齿啮合的循环以及小齿轮和大齿轮旋转的周期。

图34C表示切向综合偏差的全输出信号，经仔细选择的高通、低通和带通等滤波处理后，信号的各成分可以分开。

小齿轮所生成的长周期分量示于图34B，切向综合偏差短周期分量示于图34A。

图33在切向综合偏差图上分析长周期和短周期偏差分量

 

图34切向综合偏差图的分析，信号滤波的结果

9.3.3.3用快速富氏转换（FFT）法作数据分析

测试装置输出的信号，可直接接到一台适当的频谱分析仪作FFT分析。

图35中的线图表示一幅完整的切向综合偏差线图，以及FFT分析所得的结果。

图35一对产品齿轮检测获得的切向综合偏差的富氏分析结果

这种方式的分析是有效的，通过它可获得有关大小齿轮的各种缺陷的信息，包括切向综合偏差的长周期和短周期分量。

在作富氏分析时，为了得到充分和精确的结果，应该提供两个齿轮旋转整转数的信号。

图35所示为FFT分析得提的各主要成分的频谱图，横坐标是谐波数“n”，即相对于大齿轮的旋转频率。对各频率，必须记住齿轮噪声和振动频谱，可包括在轮齿啮合频率中一个或多个低谐和高谐的重要成分。

在本例子中，包括大齿轮8转中发出的信号，该齿轮有35个齿，这样总的轮齿啮合循环等于280。