三环减速器的动力模型及动力特性研究

5.1  引言
三环减速器是一种利用三相并列双曲柄机构来克服死点的连杆内齿行星齿轮减速器，其基本结构如图5-0所示。它由低速输出轴1 ，两根高速输入轴2 ，三片传动齿板3组成，各轴均平行配置，相同的两根高速轴带动三片传动齿板呈120°相位差作平面转动，传动环板上的内齿圈与低速轴上的外齿轮相啮合，形成大速比，其传动比

 

三环传动结构

图5-1

                                                                 （5-0）

式中
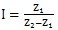
    Z₁是低速轴上外齿轮齿数；
    Z₂是齿板内齿轮齿数。
三环减速器的主要优点是：

1.传动比大、适应性广，由于采用渐开线少齿差内啮合传动，可以获得较大的传动比，单级传动比达11～99，双级传动比高达9801；又因为减速器的中心距与齿轮参数无关，可根据需要设计，故其适应性广。

2.承载能力强，且重量轻。内啮合齿轮由于接触点处齿廓曲率方向相同，所以齿面接触强度较高，同时由于少齿差传动的多齿接触承载特点，随着载荷增加，接触承载齿数也随之增加，故三环减速器有很强的承载能力和过载能力，可承受过载27倍。又由于三环减速器的结构简单，传动比大、所以其重量轻，比普通圆柱齿轮减速器重量相应减小2/3。

3.传动效率高。三环减速器的效率主要由两部分组成，即啮合效率及轴承效率。它比一般少齿差传动（K-H-V）少一个输出机构，故效率可高达96％。

4.轴承受力小，寿命长。三环减速器的行星轴承受力与K-H-V型行星轴承受力相比，K-H-V型行星轴承受力约为三环减速器的1.86倍，而行星轴承的寿命，三环的约为K-H-V型的6倍以上。

由于以上优点，三环减速器正在日益推广，目前己在矿山、冶金、石油、化工、起重运输、

经工等众多领域实际应用，取得了一定的社会效益和经济效益，通过进一步的理论分析、试验研究和技术推广，有可能成为新一代通用减速器。

但是，由于三环减速器问世仅几年时间，缺乏较全面的理论分析和实验研究，在设计只得采用类比的方法或借助于非常粗略的简化模型进行计算，设计工作缺乏依据，使得产品性能环稳定、在应用中出现发热、振动、轴承早期损坏甚至齿板断裂等现象，影响了这种传动形式的进一步发展。
本章应用本文提出的位移协调原理，从系统变形的角度，建立了三环减速器的动力分析精确模型，并针对SHQ40型三环减速器进行求解，研究了各种因素对其动力特性的影响。

5.2 三环减速器动力分析基本方程

三环减速器是三相并列双曲柄输入式的少齿差内齿行星传动装置。因此可按第三章对内齿行星传动建模方法，建立其动力分析模型。

对齿板及高速转臂轴，输出轴进行动态静力分析（见图5-2），可得三环减速器的动力分析基本方程（忽略各构件重力作用）。

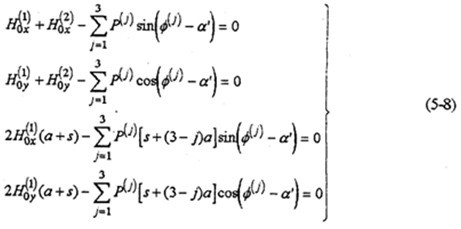
根据对三环减速器的静不定次数计算，当单轴输入（n=1）时，S=4，双轴输入（n=2）时，S=5。故应根据输入形式，由位移协调节器条件增加4个或5个动力分析补充方程。

5.3三环减速器的动力分析补充方程

三环减速是多相并列连杆行星齿轮传动过约束机构。应该从整体系统上去考虑其变形关系。图5-3是一相子机构的位移关系图。图5-3（a）是基本位置图、图5-3（b）是高速轴之间的位移关系、图5-3（c）是高速轴与输出轴之间的位移关系（i=1、2）。由图写出各运动副中心的位移关系如下：

以上各式中 ，是偏心套中心的位移；

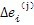
             是偏心套偏心距 变形量；

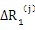
             是齿对接触点与外齿轮中心的距离变化量；

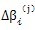
              是机构变形使高速轴产生的角位移；

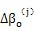
             是机构变形使低速轴产生的角位移；

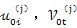
           是高速轴轴心因箱体轴承变形及轴弯曲变形产生的位移；

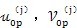
             是机构变形使啮合点产生的位移；

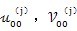
              是低速轴中心因箱体轴承变形及轴弯曲变形产生的位移；

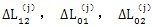
             是机构变形引起各运动副中心之间的距离产生的相对位移量；

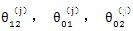
              是各运动副中心连结因机构变形产生的角位移。

式中

当只考虑行星轴承变形和内齿圈变形时，式（5-18）及（5-19）就变成（3-11）、（3-14）。

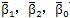
上式的第一式即为高速轴之间的约束条件，第二式为高速轴与低速轴（输出轴）之间的约束条件，消去试中的 可得4个补充方程，满足单轴输入（n=1）所需的动力分析补充方程的数量（S=4）。对于双轴输入（n=2），若分流机构为齿轮传动，则由式（3-12b）增加一个补充方程得

 

由式（5-18）、（5-19）、（5-22）、（5-23）就构成三环减速器的动力分析补充方程。将它们与三环减速器的动力分析基本方程联解，可以确定出的运动副的动反力及齿板、轴等的变形角位移，随转角（或时间）的函数关系。各齿板、轴的角位移与转角φ的关系可表示成：

上式是三环减速器转动时，各齿板、轴在机构变形时的角位移关系式，将其求导（对时间）可得角速度、角加速度关系。

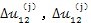
式（5-18）中的为机构变形后两偏心套中心之间的长度L₁₂产生的增量分量，它包括齿板两高速轴孔之间的相对变形量，两行量轴承的变形量，两偏心套的变形量以及两运动副的间隙等。可表为

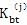
式中  是齿板高速轴孔周边变形刚度，见表4-3；

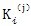
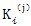
      是行星轴承变形刚度，由文献， =4.48×10⁵N/mm；

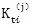
      是偏心套外圆周边变形刚度，见表4-1；

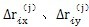
      是运动副间隙在x、y方向的分量。

表4-3 

表4-1 

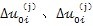
式（5-19）中的 是啮合接触点p与偏心套中心的距离因机构变形产生的变形增量。它包括齿板啮合接触点与高速轴孔中心的相对变形量、行星轴承的变形量、偏心套的变形量以及运动副间隙、轮齿齿形误差等。可表示为

式中

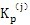
是齿圈变形刚度，见表4-2；

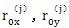
是齿形法向误差在坐标轴方向的分量；

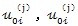
是高速轴轴心的位移，它是由由箱体轴承变形及轴的弯曲变形引起的，即

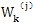
式中 由（4-63）计算。

表4-2

 

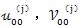
低速轴轴心位移 也是由箱体轴承变形及低速轴弯曲变形组成。但由于低速轴的法向尺寸较大、弯曲变形很小，故可忽略不计，只考虑箱体轴承的变形则有

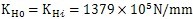
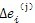
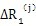
式（5-27）及式（5-28）中s是两则齿板靠近箱体的距离，a是齿板之间的距离。取箱体轴承的刚度 。偏心套的径向变形 以及外齿轮的径向变形 均很微小，故一般忽略不计。

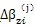
高速轴的扭轴变形 由式）（4-59）计算。低速轴因径向尺寸比高速轴的远远大，故其变形可忽略不计。

5.4三环减速器的载荷分布

三环减速器的载荷有啮合力、行星轴承载荷以及箱体轴承载荷。其分布情况直接反映出三环减速器的动力学性能。下面分析SHQ40型三环减速器的载荷分布特性。SHQ40的有关参数为

i=20    z₁=60   z=63   m=4   e=6.392mm   a′=28.1⁰   a=20⁰   T=4000Nm    n=1000rmp    L₁=400mm     L₂=210mm    B=30mm    s-55mm     d=34mm

在不计各种误差且机构变形很小时，将以上参数代入三环减速器的非线性动力分析方程式（5-1）～（5-8）、（5-18）、（5-19）、（5-22）～（5-23）等方程，在计算机上求解，就可求得三环减速器各载荷随工况角φ的变化规5-4为计算程图。

5.4.1  啮合力分析规律

SHQ40型三环减速器的啮合力随φ的变化规律如图5-5所录。由图可以看出啮合力的以下规律：

1.三片齿板上对应的啮合图变化规律完全机同，彼此相位差为120°，以360°为击期限变化。

2.无论在什么工况三片齿板的啮合力之和总为常数，但各片齿板的啮合力并不一定相等。即

3.在一个周期内，各齿板的啮合力均各取得两次数值不等的极小值和两次数值相近的极大值。第一片齿板的极值点为

               

              

理想情况下，啮合力的极小值在φ=0°、180°产生，极大值在φ=90°、270°产生，造成位置偏离的影响因素主要有轴承刚度，齿板刚度，啮合角以及输入转速、传动比等等。其中轴承刚度的影响极大。在死点的啮合力也产不并一定为零。哈合力可能为负值。为负值时，将阻碍传动的正常转动，产生内齿轮副的干涉现象。并引起减速器冲击振动。因此，按照啮合力过死点时为零的假设分布规律以及啮合力为常数分布规律的模型分析，所得结果都是不可靠的。图5-6是齿板死点位置180°及另一齿板位于超前120°啮合点的单齿啮合图的测试结果。图中每一棒线代表被测齿受啮合力作用一次。比较两图可知，死点位置啮合力总体水平低于120°位置时的啮合力总体水平，与理论分析计算的结果完全吻合。

4.将各齿板过死点时的啮合力整理成表，见表5-1所示。

表5-1  齿板过死点时的啮合力分布

由表看出，各齿板过相同死点位置之不理时的啮合力相等；某片齿板过死点位置时，其它两片齿板超前或者范后干该片啮合120°与水平轴对称。因此，这两片的啮合力相等，从图5-4也反映了这一点，这与实际情况相符合。

5.4.2高速轴行星齿轮减速器中，行星轴承受力大，寿命短，摩擦损耗大，是减速器的薄弱环节。因此，减小轴承载荷，提高行星轴承的寿命，一直是人们力求解决的问题。SHQ40型三环减速器的行星轴承动载荷，提高行星轴承的寿命，一直是们力求解决问题。SHQ40型三环减速器的行星轴承动载荷分布规律，见衅5-7、图5-8、图5-9所示。由图可行出以下结论：

1.三片齿板上对应的行星轴承荷变化情况完全相同，彼此相位差120°，以360°为周期变化。

2.无论是输入轴还是支承轴X方向的行星轴承载荷比y方向的要大，且一周内出现正负两次峰值。这说明行星齿板在水平方向因动载荷产生的振动比垂直方向大。

3.由图5-8可知，支承轴行星轴承在过死点时的y向轴承载荷（切向力）并不为0，说明某相机构在过死点时，是由其它两相机构通过支承从动轴传递扭矩带动该相机构通过死点的。因此，孤立地分析研究一相子机构将偏心套简化为二力杆件建立的模型是不可靠的。

4.输出轴的行星轴承总体载荷比支承轴行星轴承总体载荷大（图5-9），特别是输入轴X方向受力最大。输入轴行星轴承载荷在死点附近取得最小值，在φ=105°、255°取得极大值。极大值产生的位置正好是机构传动角最佳位置附近。在同一时刻，齿板上各输入轴行星轴承的受力状况是不是一样的。当某一齿板接近其死点位置时，轴承载荷较小，而同时另外两片远离死点位置的齿板上输入轴行星轴承载荷要大得多。支承轴的轴承载荷在一个周期内分别出现三次极大值和三次极小的值。由于这个原因使支承轴偏心套的微动磨损比输入轴偏心套的微动磨损更为严重。行星轴承载荷的最大值为

F_1max=40662.733713N       φ=255⁰

F_2max=32274.64763N        φ=125⁰

根据轴承的寿命计算，三环减速器与K-H-V型少齿差行星减速器相比，K-H-V型的行星轴承当量动载荷约为三环式的1.86倍，而轴承受命，三环式的约为K-H-V型的6.33倍以上。

5.4.3箱体轴承载荷的分布规律

箱体轴承载荷的分布曲线如图5-10、5-11、5-12的所示。

总体说来，箱体轴承载荷比行星载荷变化要平缓一些；输入轴的箱体承载荷幅值比支承轴的大1倍以上，比输出轴的大3.8倍以上。由于各轴的载荷分配不均等现现象，也将使减速器产生振动。各轴的箱体轴承载荷的最大值为

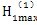
输入轴   =28513.0064N   φ=15

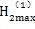
支承轴   =-32149.23N    φ=15

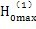
输出轴   =12587.355N    φ=15

5.5影响三环减速器动力特性的因素

影响三环减速器的载荷分布特性的参数主要有输入轴扭矩、转速、啮合角、传动比、轴承刚度、齿板齿圈刚度以及偏心套或齿板的结构参数等。了解这些参数对三环减速器动力性能的影响，对正确设计三环减速器具有重要意义。

5.5.1 输入参数的影响

输入参数包括输入扭矩、输入转速。这两个参数对三环减速器的影响很大。现有的三环减速器用于高速重载时，产生的振动和噪声都非常大、输入扭转的影响可由式（5-4）分析。

当n=1   即单轴输入时

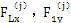
由上式可知，当减速器几何参数一确定，e及r₂均为已知参数。因此增大M，必须引起左边的行星轴承载荷 增大使方程式（5-30）平衡。图5-13是输入扭矩分别为150N.m及200N.m时的啮合图。由图可看出，负载增加，啮合力幅值增大。采用双轴输入时可降低各载荷的幅值，使其均衡化。图5-14是单轴输入时的啮合力及行星轴承载荷。图5-15是双轴输入时的啮合力及行星轴承载荷。从两图比较得知，无论是啮合力，还是轴承载荷，采用双轴输入后其变化均趋于平缓，幅值降低很多，三相啮合力趋于均衡，而且负向啮合力已消除。

 

输入扭矩对减速器的静态载荷产生影响，而转速是对动态载荷产生影响。图5-16是输入转速对减速器的载荷影响情况。转速越大，三相啮合力越不均衡，当转速超过1500rpm后，第三相齿板与外齿轮的啮合力变成负值。负向啮合力将阻碍输出轴的转动，使内啮合副产生干涉。第一片齿板的啮合力最大，幅值随转速的增加而增加。从行星轴承载荷看，转速小于1600rpm时载荷较均衡，大于1600rpm后，随转速加大，其幅值变大。

5.5.2结构参数的影响

当三环减速器各轴之间的中心距确定后，影响其动力性能的主要结构参数有偏心距、压力角、齿数差（或传动比）以及偏心套外圆半径、内齿板高速轴孔大小（或行星轴承尺寸）等等。设计时，不能孤立地考虑这些参数，它们之间存在相互影响的关系。偏心距由压力角、齿数差（或传动比）决定，即：

由上式知，当齿数差Z₂-Z₁越小或传动比i越大时，偏心距e越小；压力角越大时，偏心距e越大，则选用的行星轴承尺寸大，齿板高速轴承孔径也就大。图5-17是传动比、压力角、以减速器行星轴承载荷的影响。由图可见，传动比的变化对减速器的动力性能影响极大；传动比越大，则偏心距越小。由式（5-30）分析得，行星轴承载荷必须大。压力角的变化，对行星轴承载荷影响小得多。

图5-18是偏心套外径对啮合图的影响。当不考虑偏心套外径（r₂=0）时，啮合力分布为正值。考虑偏心套外径（r₂=37.5mm）计算结果，出现负向啮合力。而且其幅值明显增大。输入扭矩也不再是固定值。因此，对三环减速器进行动力计算，必须考虑r₂的影响。此外，行星轴承内外圈接触承载位置，也影响三环减速器的动力性能。

5.5.3刚度的影响

只考虑行星轴承变形及齿板变形时，影响三环减速器载荷特性的刚度，主要是行星轴承刚度、和内齿圈的变形刚度。轴承刚度与轴承材料、间隙、油膜等很多因素有关。图5-19是输入轴行星轴承刚度对啮合力及行星轴承载荷的影响。当输入行星轴承刚度小一个数量级时，负向啮合力区域增大（见图5-19a）；随刚度减小、各相啮合力越不均恒（图5-19b），输入轴行星轴承刚度的影响比输入轴行星轴承刚度更大，见图5-20所示。啮合力及各行星轴承载荷在轴承刚度较小的情况时，都出现正常载荷的10倍以上的冲击现象，冲击产生的位置随刚度变化不同。内齿圈刚度对载荷的影响与行星轴承刚度相反（见图5-21所录）。当刚度越小时，三相齿板的啮合力越均恒（见图5-21a），而且行星轴承载荷幅值基本上不变（见图5-21b）。同此可推知，减小三环减速器振动的途径之一就是提高行星轴承刚度，减小内齿圈刚度。这可以通过对行星轴承进行预紧，和采用软齿面或大柔度齿圈的办法，以使啮合力和行星轴承载荷均衡化，以达到减振降噪的目的。

5.6三环减速器的轴间布置

三环减速器的特点之一就是适应性强，只要保证输入与输出的中心距要求，就可以任意调整支承轴，以满足各种空间要求，但各轴间的相对位置不同，对其动力特性的影响各异。

5.6.1 各轴水平布置时的载荷分布特性

各轴水平布置时，轴间的中心距变化，将引起各载荷大小幅值、规律均发生变化。图5-22是输入轴相对输出轴位置变化时，减速器的啮合力及轴承载荷变化情况。由图可知，当输入轴与支承轴中心距（L₂=200mm）很小时，三齿板的啮合力分配很不均衡，随着L₁的增加啮合力趋于均衡（见图5-22a）。行星轴承载荷变化情况见图5-22b所示。

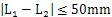
当 时，载荷产生冲击为无穷大，L₁≥400mm以后，随着L₁的增加，三相行星轴承载荷幅值变化很缓慢，接近于直线分布。但箱体轴承载荷的幅值在L₁>350mm后，随L₁增加各相之间的幅值差变大，趋于不均衡状态（见图5-22c）。因此SHQ50型及SHQ63型的三环减速器的振动比SHQ40型的大。

支承轴的位置L₂变化的载荷分布规律与输入轴位置L₁变化的载荷分布规律相似（见图5-23所示），但当L₂后各相载荷之间的幅值差比L₁变化时要小很多，故各相之间的载荷分配比较均衡。这是因为L₂> L₁=200mm以后，减速器为中轴输入。中轴输入时，无论是啮合力还是轴承载荷的分布特性都较好。各相载荷分配也比较均衡。

5.6.2各轴任意布置时的载荷分布特性

当输入轴与轴出轴的中心距确定后，可通过调整支承轴的位置，满足特殊的空间位置要求，或者设计成载荷分布特性最优、幅值最小的减速器。图5-24是中心距L₁=400mm、L₂200mm时，支承轴相对于输出轴转动的角位移 变化时啮合力及行星轴承载荷的分布情况。由图看出，各种载荷均在180°附近（SHQ偏置式减速器）取得极大值。在0°～90°和270°～360°范围（Ⅰ、Ⅳ限内），三相齿板啮合力分配很均衡，啮合冲击很小。因此。设计三环减速器时，为减小载荷的幅值和各相之间载荷的差值、支承轴应尽可能远离180°，即不采用三轴心共线的水平位置的结构。图5-25为几个特殊位置的啮合力随转角变化的分布规律。