4.5 角向不对中时的联轴器的工作状态
角向不对中时，由于两轴之间存在一定的夹角，使得橡胶圆环最上方受到附加的拉应力，而圆环的最下端则受到附加的压应力，这个附加的拉应力σang的大小和方向随着圆环的旋转角度改变而改变，在最上方时受拉，且绝对值最大，在最下方受压，绝对值亦最大，所以其变化的过程图形类似于余弦函数；由橡胶圆环旋转扭矩产生的剪应力τrot方向始终与其线速度方向相反，而线速度方向在旋转一周的过程中不断的变化。角向不对中时的应力情况应该是σang与τrot的叠加。所以其受力情况比较复杂。分别取四个象限点的位置状态作为研究重点，分别对单元体进行应力分析。
(1）角向不对中900位置：当圆环上的单元体旋转到最上方时，也就是900位置时，单元体的应力如下图所示
此时的受力情况其实属于二向应力状态，即为拉扭结合，
此时主平面上的正应力平面的角度有这种关系
应力平面如图4.24所示。此时的最大应力值为
（2）角向不对中180°位置：当圆环上的单元体旋转到最左端时，也就是180°位置时，单元体的应力如下图所示
此时的受力图中可以看出，附加的拉应力已经减小为零，实际上单元体受力其实属于纯剪切状态，
此时主平面上的正应力平面的角度有这种关系：tg2α2=-∞，所以有α2=-45°或-135°，最大主应力值为σmax=30MPa
（3）角向不对中270°位置：当圆环上的单元体旋转到最下方时，也就是270°位置时，单元体的应力如下图所示
此时的受力情况其实属于二向应力状态，只是这时的附加应力变成了压应力。即拉应力变成了负号。利用拉扭结合时的应力分析方程可知
（4）角向不对中360°位置：当圆环上的单元体旋转到最右端时，也就是360°位置时，单元体的应力如下图所示
此时的受力图中可以看出，附加的拉应力已经减小为零，实际上单元体受力其实属于纯剪切状态，
此时主平面上的正应力平面的角度有这种关系：tg2α4=-∞，所以有α4=-45°或-135°，此时的最大应力值为σmax=30MPa
通过角向不对中的分析可以知道，具有角向不对中的联轴器受力情况仍然属于两向应力状态，即只有拉扭结合与纯剪切的情况发，没有三向应力状态，比较四个位置的最大主应力
可以知道，在联轴器旋转一周的过程中，最大主应力在90°位置。即90°位置为角向不对中时的危险点。
4.6 综合不对中时的联轴器的工作状态
综合三种不对种情况，对圆环的单元体进行综合受力分析。由于实际工作中联轴器两轴之间不仅存在一定的径向和轴向位移，而且存在一定的偏角。使得橡胶圆环受到附加的轴向拉应力σax，附加的径向剪应τrad，附加的角向应力σang，以及由橡胶圆环旋转扭矩产生的剪应力τrot。所以综合不对中的应力情况应该是σax、τrad、σang与τrot的叠加。所以其受力情况比较复杂。仍然按照上面类似的方法分别取四个象限点的位置状态作为研究对象，分别对单元体进行应力分析。
(l）综合不对中90°位置：当圆环上的单元体旋转到最上方时，也就是90°位置时，单元体的应力如下图所示
此时的应力情况属于三向应力状态，所以其分析过程和径向不对中90°以及270°以情况相似，只是这里还有了附加的轴向拉应力和附加的角向应力，将各个应力值σxx=σax+σang，σyy=0，σzz=0，τxy=τrot，τyz=0，τzx=τrad分别代入式（4-29）（4-30）（4-31）中，可以得到
I1=σax+σang+0+0=σax+σang
I2=0+0+0-
-0-
=-
I3=0-0-0-0+0=0
再将三个应力不变量代入方程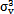
- I1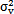
+ I2σv- I3=0中，得到
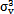-（σax+σang）-（
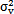）σv=0 （4-48）
解出这个方程，可以得到三个主应力的值
上一页
下一页
