5.4 非线性静力分析
5.4.1 非线性分析要注意的问题
通过比较小心地采用时间和方法,可以避免许多和一般的非线性分析有关的困难,一般从以下几个方面考虑:
1.了解程序的运作方式和结构的表现行为
在使用大的,复杂的模型前,构造一个非常简单的模型(也就是说仅包含少量单元),以及确保理解如何处理这种特性。通过首先分析一个简化模型,以便对结构的特性有一个初步了解。对于非线性静态模型,一个初步的线性静态分析可以知道模型的哪一个区域将首先经历非线性响应,以及在什么载荷范围这些非线性将开始起作用。对于非线性瞬态分析,一个对梁,质量块及弹簧的初步模拟可以使你用最小的代价对结构的动态有一个深入了解。在着手最终的非线性瞬时动态分析前,初步非线性静态,线性瞬时动态,和/或模态分析同样地可以有助于理解结构的非线性动态响应的不同的方面。
阅读和理解程序的输出信息和警告。至少,在尝试后处理结果前,确保问题收敛。对于与路程相关的问题,打印输出的平衡迭代记录对确定结果是有效还是无效方面是特别重的。
2.简化模型
尽可能简化最终模型。如果可以将3-D结构表示为2-D平面应力,平面应变或轴对称模型,那么就这样简化;如果可以通过对称或反对称表面的使用缩减模型尺寸,那么就这样简化;如果可以忽略某个非线性细节而不影响模型的关键区域的结果,那么这样简化。只要有可能就依照静态等效载荷模拟瞬时动态加载。
考虑对模型的线性部分建立子结构以降低中间载荷或时间增量及平衡迭代所需要的计算时间。
3.采用足够的网格密度
考虑到经受塑性变形的区域要求一个合理的积分点密度。每个低阶单元将提供和高阶单元所能提供的一样多积分点数,因此经常优先用于塑性分析。在重要塑性区域网格密度变得特别地重要,因为大挠度要求对于一个精确的解,一个单元的变形(弯曲)不能超过30度。在接触表面上提供足够的网格密度以允许接触应力以一种平滑方式分布。
提供足够用于分析应力的网格密度。那些应力或应变关心的面与那些需要对位移或非线性解析处的面相比要求相对好的网格。
使用足够表征最高的重要模态形式的网格密度。所需单元数目依赖于单元的假定位移形状函数,以及模态形状本身。
使用足够可以用来分析通过结构的任何瞬时动态波传播的网格密度。如果波传播重要的,那么至少提供20个单元来分析一个波长。
4.逐步加载
对于非保守的,与路径相关的系统,你需要以足够小的增量施加载荷以确保你的分析紧紧地跟随结构的载荷响应曲线。
有时你可以通过逐渐地施加载荷提高保守系统的收敛特性,从而使所要求的Newton_Raphson平衡迭代次数最小。
5.合理地使用平衡迭代
务必允许程序使用足够多的平衡迭代(NEQIT〕。在缓慢收敛,路径无关的分析中是特别重要的。
相反地,在与路径严重相关的情况下,可能不应该增加平衡迭代的最大次数超过程序的缺省值。如果路径相关问题在一个给定的子步内不能快速收敛,那么求解可能偏离理论载荷响应路径太多。这个问题当时间步长太大时出现。通过强迫分析在一个较小的迭代次数后终止,这时可以从最后成功地收敛的时间步重新起动(ANTYPE),建立一个较小的时间步长,然后继续求解。打开二分法(AUTOTS,ON)会自动地用一个较小的时间步长重起动求解。
6.克服收敛性问题
如果问题中出现负的主对角元,计算出过大的位移,或者仅仅没能在给定的最大平衡迭代次数内达到收敛,则收敛失败发生。收敛失败可能表明出结构物理上的不稳定性,或者也可能仅是有限元模型中某些数值问题的结果。ANSYS程序提供几种可以用来在分析中克服数值不稳性的工具。如果正在模拟一个实际物理意义上不稳定的系统(也就是具有零或者负的刚度),那么将拥有更多的棘手问题。有时你可以应用一个或更多的模拟技巧来获得这种情况下的一个解。
7.打开自动时间步长
当打开自动时间步长时,往往需要一个小的最小的时间步长(或者大的最大的步长数)。当有接触单元(如CONTACT48,CONTACT12,等等)时使用自动时间分步,程序可能趋向于重复地进行二分法直到它达到最小时间步长。然后程序将在整个求解期间使用最小时间步长,这样通常产生一个稳定但花费时间的解。接触单元具有一个控制程序在它的时间步选择中将是多么保守的选项设置(KEYOPT),这样,允许你加速在这些情况下的运行时间。
对于其它的非线性单元,需要仔细地选择你的最小时间步。如果选择一个太小的最小时间步,自动时间分步算法可能使运行时间太长。相反地,最小时间步长太大可能导致不收敛。
务必对时间步长设置一个最大限度((DELTIM)或者(NSUBST)),特别是对于复杂的模型。这确保所有重要的模态和特性将被精确地包含进去。这在下列情况下可能是重要的。
具有局部动态行为特性的问题(例如,涡轮叶片和轮毂部件),在这些问题中系统的低频能量含量以优势压倒高频范围。具有很短的渐进加载时间问题。如果时间步长允许变得太大,载荷历程的渐进部分可能不能被精确地表示出来。包含在一个频率范围内被连续地激励的结构的问题(例如,地震问题)。当模拟运动结构(具有刚体运动的系统)时注意。分析输入或系统驱动频率所要求的时间步通常比分析结构的频率所要求的大几个数量级。采用这样粗略的一个时间步会将相当大的数值干扰引入解中,求解甚至可能变得不稳定。
5.4.2 轴向不对中模拟
考虑到两块钢板的刚度比橡胶的刚度大得多,钢板与橡胶圆环之间为粘结,圆环与钢板之间不会产生滑动。因此可以进行模型简化。只建立像胶块的模型。有考虑到在由于模型对称性和载荷的均布特征,在建立模型时只需要建立一部分实体的模型。轴向不对中时取圆环的1/2部分作为分析对象。联轴器的有关参数为:
密度:10O0kg/m3
弹性模量:E=l.27e9Pa
泊松比:v=0.47
稳定状态的转速1800rad/min
(l)定义单元类型
考虑到分析橡胶材料所能用到的单元,选择Main Menu>Preprocessor>Element type>Add/Edit/Delete,在出现的对话框中,单击“Add”,如图5.7所示。这时又出现一个“Library of Element Type”对话框,在左面的列表栏中选择“Structural Solid”,在其右面的列表栏中选择“2Onode186”,单击0K按钮,如图5.8。再在单元对话框中单击Close按钮关闭对话框。

(2)定义材料属性
参照联轴器的Mooney-Rivlin的常数,并在Define Material Model Behavior框中操作Strctural>Nonlinear>Elastic>Hyperelastic>Mooney-Rivlin>2 parameters.在弹出的所示Hyper-elastic Table对话框中输入“C10=1.41e6”“C01=0.023e6”。并单击确定按钮。其结果如图5.9,5.10所示

(3)建立截面模型
选择Main Menu>Preprocesor>Modeling>Create>Keypoints>In Active CS,在弹出的对话框中输入1关键点的坐标,如图5.11所示。单击“Apply”输入下一个点的坐标直至所有关键点完全输入。6个关键点的坐标如表5.1所示。
表5.1 关键点的坐标
| 坐标值/关键点 |
1 |
2 |
3 |
4 |
5 |
6 |
| x |
0 |
0 |
0 |
0 |
0 |
0 |
| y |
0 |
0 |
132.5 |
132.5 |
149 |
149 |
| z |
0 |
55 |
0 |
55 |
0 |
55 |
选择Main Menu>Preprocessor>Modeling>Create>Areas>Arbitrary>Through KPs,通过关键点3,4,5,6生成平面截面,结果如图5.12所示
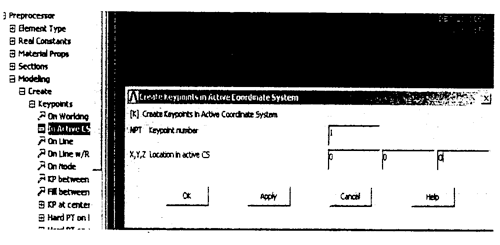
图5.11 在坐标系中创建关键点

(4)生成三维模型
由2D拖拉生成3D,选择Main Menu>Preprocessor>Operate>Extrude>About Axis,出现一个拾取框,单击“Pick All”,又拾取轴线的关键点即编号为“1,2”的关键点,在“Arc length in degree”后面的输入栏中输入圆弧角“-180”度,输入“NSEG=8”即生成的实体由八块体积组成。改变视图方向,看到的ISO图形为图5.13
(5)划分网格
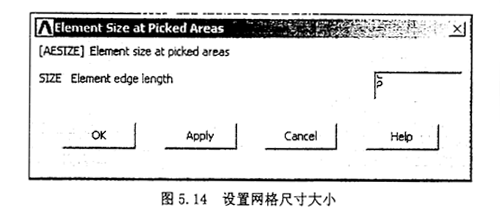
采用影射网格生成单元,Mesh Tool下设置面上网格尺寸的大小,橡胶圆环内外端面的尺寸设为30,两个截面尺寸设为5。在“Mesh”工具条下“Shape”下选择“Hex”“Mapped”,单击“Mesh”,在图形屏幕上选择实体。单击“OK”,生成的网格单元如图5.15所示

上一页
下一页






