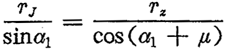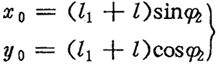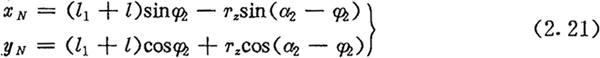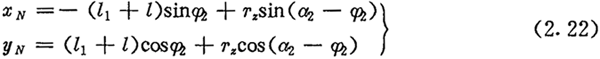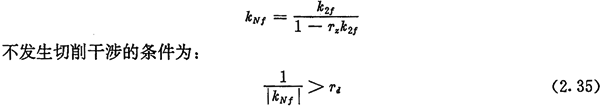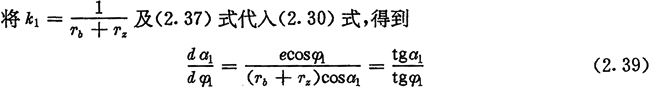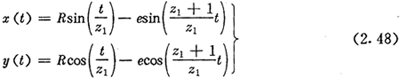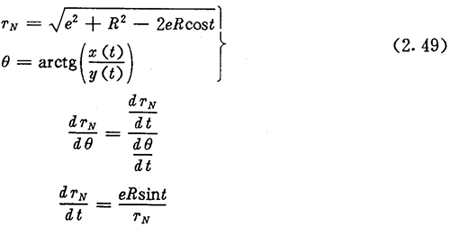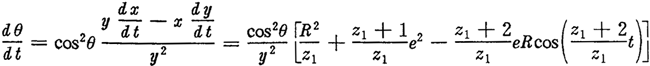这样（2.17）式中的μ可表示为：

由图2.5（或图2.6）中的△OM₁O₁还可得

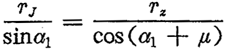
整理后为：

按关系式（2.16）可计算出外滚子工作角a₂

而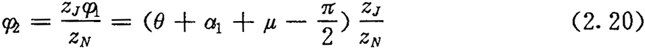

对于图2.5所示正向结构，在与内齿圈固联的坐标系中，得到外滚子中心轨迹H₂的方程为：

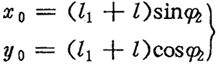
及内齿圈齿廓H_N的方程为：

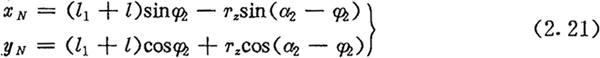
对于图2.6所示的反向结构，在坐标系（0，x_N，y_N）中，得到内齿圈齿廓的方程为：

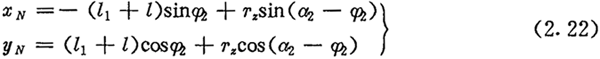
每给定一个θ值，由激波器廓形方程式计算出T_J, 接着计算dT_J/dθ及μ，然后把由(2.17）式算出的l₁的值和由（2.19）式算出的α₁的值代入（2.16）式，可算出相应的α₂，由式（2.20）便可得到φ₂，最后把这些值代入（2.21）式（反向结构代入（2.22)式），便可得到内齿圈齿廓上相应的一个点M₂的坐标值（x_N，y_N）。当θ在激波器的一个周期内取一系列点时，相应的M₂点描绘出内齿圈齿廓上一段工作齿廓与非工作齿廓曲线的图形。

由上面可以看出，在选定激波器廓形T_J=T_J（θ）的情况下，正反两种结构所得到的内齿圈齿廓方程式（2.21）与式（2.22）在形式上是不同的。对于反向结构，用-θ代换激波器方程中的θ，即令T_J=T_J（-θ），则θ增加的方向为顺时针方向，若激波器廓形可表示为偶函数，即T_J（—θ)=T_J（θ），让激波器按逆时针方向转动，则所得的内齿圈齿廓方程式完全与（2.21）式相同。因而齿廓方程式（2.22）与式（2.21）虽然形式不同，但实质是一样的。区别在于参数吸的取值方向，今后以式（2.21）作为内齿圈齿廓的标准形式。

2.4.2内齿圈齿廓的曲率及曲率干涉的校核
内齿圈齿廓曲线上某点的曲率，表示该点附近齿廓曲线的弯曲程度，反映了齿廓曲线的几何特性，是研究机构性能的重要参数。前面说过，内齿圈的齿廓H_N与外滚子中心轨迹H₂是法向等距线，它们在相应点的曲率有一定的关系，所以要求H_N的曲率，可以先求出外滚子中心轨迹H₂的曲率。
根据微分几何，外滚子中心轨迹H2的相对曲率k₂可由下式计算：

由（2.5）式可得：

这样，由（2.24）式便可得到在外滚子中心轨迹上与激波器任一角度θ对应点的相对曲率k₂，而内齿圈齿廓H_N上对应点的曲率k_N为

在对应于内齿圈的齿顶部分，当曲线H₂的最小曲率半径P_min小于或等于滚子半径时，即P_min≤T_Z时，则内齿圈齿廓曲线H_N在齿顶处发生交叉，结果使齿顶变尖，称这种现象为顶切。顶切将使机构的传动特性受到影响，使同时参加工作的推杆数目降低。由（2.24）式可计算出曲线H₂在对应于齿顶处的相对曲率k_2a，不发生顶切的条件为：

另外，当选用半径为T_d的刀具加工内齿圈齿廓时，在齿根处可能发生切削干涉（过渡切削）。同样由式（2.24）可计算出曲线H₂在对应于齿根处的相对曲率k_2f，齿廓曲线H_N在齿根处的相对曲率k_Nf为：

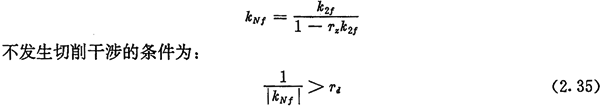
2.4.3 激波器为偏心圆的机构目前见到的推杆减速器，其激波器廓形都为偏心圆。设激波器廓形的半径为T_b，偏心距为e，由于接触点的法线O₁M₁必然通过偏心圆的几何中心，如图2.7所示，所以不需要列出激波器廓形的方程，而直接从几何关系就能计算出滚子工作角。

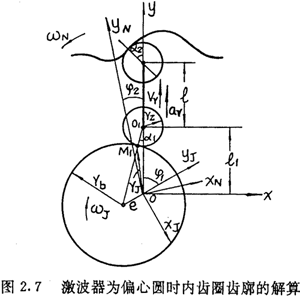
将它们代入（2.19）式，便得到（2.37）式。可见前面所得到的多激波计算公式对激波器为偏心圆的单激波也同样适用。在单激波情况下，内外滚子工作角之间的关系简化成了：

式（2.36）、（2.37）、（2.38）是偏心圆激波器的推杆减速器中l₁、a₂与φ₂的基本关系式，后面常用到它们。

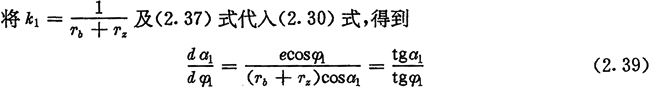
代入（2.24）式及（2.21）式就可求得H₂的曲率及内齿圈齿廓H_N的方程。
当l=0时，内外滚子合而为一，这时的推杆活齿传动机构成了滚柱活齿传动机构，所以上面的各公式对滚柱活齿传动机构也适用，只需将其中的l=O即可。
2.5由内齿圈齿廓反求激波器廓形
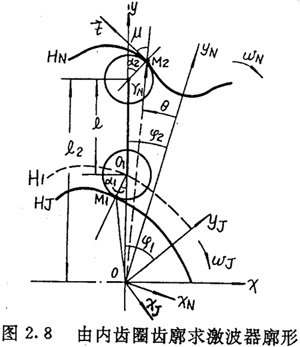
设选定内齿圈齿廓H_N的方程为T_N=T_N（θ），θ 增加的方向为逆时针方向，当内齿圈N相对传动圈转过角度φ₂时，对应于激波器相对传动圈转过的角度为φ₁，如图2.8所示。设此时H_N与外滚子在M₂点接触，同样由微分几何，内齿圈齿廓曲

2.6 应用举例

设选定推杆减速器内齿圈齿廓为一外摆线，其方程为：

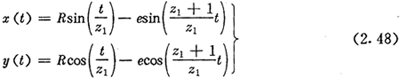
取e=5mm，z₁=11，R=120mm，用外摆法形成此曲线时，R表示基圆与发生圆半径之和，e表示定点离发生圆圆心的距离。取推杆长度l=36mm，滚子半径T_z=10mm，求单激波时的激波器廓形。

由z₁=11知内齿圈为11个齿，即z_N=11。将摆线化成极坐标方程就是

上式中：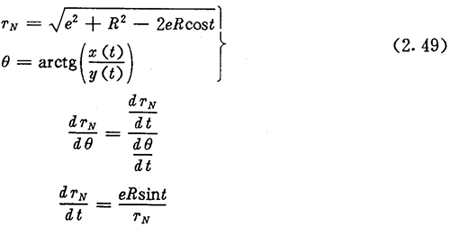

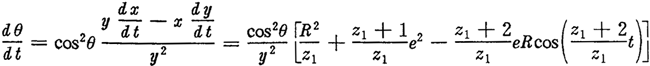
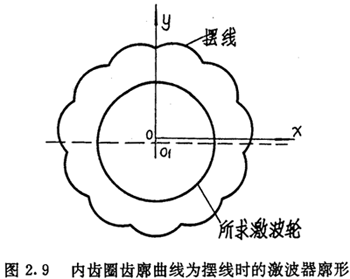
每给一个t值，按上述式子可算出相应的T_N及θ，经（2.40）式可算出μ, 然后由式（2.41）、（2.42）、（2.43）和（2.45）算出相应的l₂、a₂、a_l及φ₁。最后由式（2.47）可算出激波器廓形H_J上对应点的坐标值。一些点的计算数据如表2.2所示，由计算机绘出的激波器廓形如图2.9所示，它并不是一个标准的圆，图中圆的上部稍微有点凸出。由解的唯一性可推知，激波器为偏心圆的推杆减速器，其内齿圈廓形一定不是摆线，虽然形状相似，其实二者是不同的，这已为工程实际所证实。

表2.2 激波器廓形的计算值

t°	a°2	a°1	xJ	yJ
0.000000 30.000000 60.000000 90.000000 120.000000 150.000000 180.000000 210.000000 240.000000 270.000000 285.000000	>0.000000 23.650020 31.001688 28.389094 20.971822 11.056220 -0.0000000 -11.056620 -20.971822 -28.289094 -30.519488	0.000000 3.409274 4.711771 4.291084 3.086500 1.591049 -0.000000 -1.591049 -3.086500 -4.291084 -4.69190	0.000000 -16.120000 -33.691177 -50.008323 -55.717625 -38.800958 -0.000000 38.800958 55.717652 50.008323 42.427781	63.166667 60.433124 50.604335 30.005329 -2.549328 -37.372742 -53.166667 -37.372742 -2.549328 30.005392 41.871237

上一页

下一页