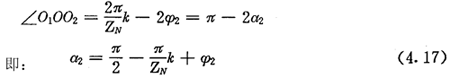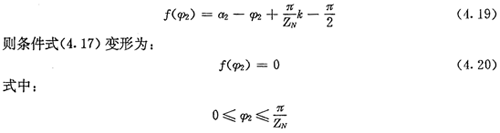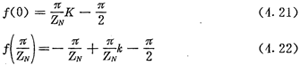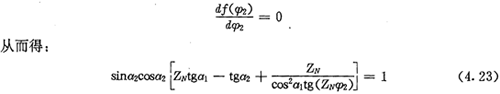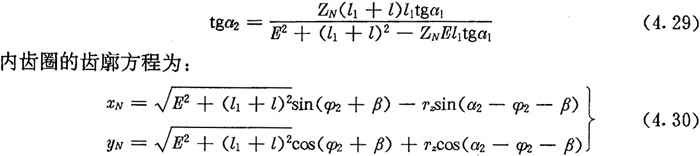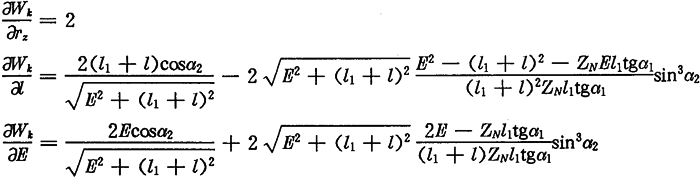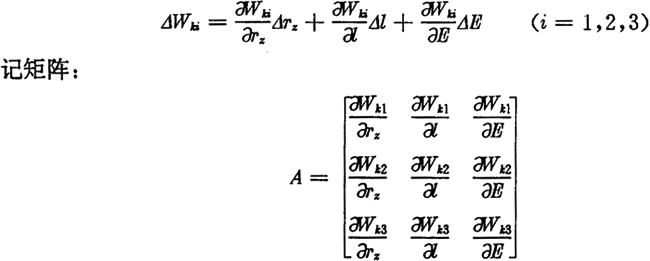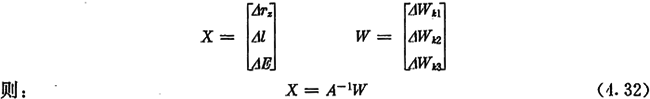c.齿根段的修形
给定齿根修形角φf和径向最大修形量△lf,选择移距增量函数:

同样可以证明,齿根修形曲线与中段修形曲线也是光滑连接的。
4.3.4修形对工作推杆数的影响

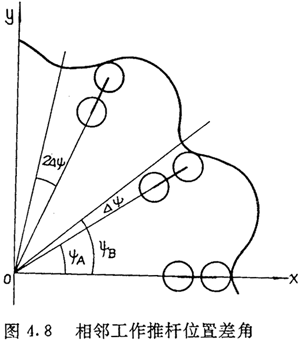

显然,未经修形的齿廓曲线在齿顶邻域和齿根邻域啮合的压力角都很小,因而分段修形后应将顶、根部大致削去相同的区段。即φa、φf仰的分配应根据各自所对应的顶根段曲线弧长相等的原则来进行。一般可近似取φa为φf的2到4倍,而取△la=△lf=esinφa。
[计算实例]:
对于TW-3-16推杆减速器,要求内齿圈齿廓经修形后同时工作的推杆数ng不少于5,按上述方法确定的修形量为:
φa+φf=4.5°
取φa=2φf,则φa=3°,φf=1.5°,△la=0.36mm选择△TZ=0.19mm,将齿廓分段修形后,机器性能得到了明显改善。
4.4内齿圈齿廓的公法线测量及加工精度控制
目前在推杆减速器的大批量生产中,对内齿圈齿廓的加工所采用的还都是范成加工方法,其测量手段长期以来一直没能得到很好的解决。一些生产厂家主要是利用测量齿根至齿圈外圆的厚度及齿顶至齿圈外圆的厚度来确定被加工齿廓的合格与否。这种方法并没有能够完全反应出内齿圈齿廓在加工过程中所产生的误差,它仅毙反应出偏心距的误差。公法线测量法是以预先计算出的公法线理论长度为依据,根据测量的结果,能够判断出加工过程中影响内齿圈齿廓加工精度的各个控制参数所产生的误差,从而对这些参数进行调整,使之达到要求的精度。
4.4.1公法线的长度计算
如图4.9 所示,AB是其中一个齿槽的一侧齿廓,A′B′是跨槽数为K(图中k=4)的一个齿梢的另一侧齿廓,它们是两个性质不同的齿廓。若把AB看成是工作齿廓,则A′B′是非工作齿廓。选择图4.9所示的坐标系,让坐标原点O与内齿圈几何中心重合,y轴与OA重合。设P(x,y)为AB齿廓上的一点,在P点与内齿圈齿廓相接触的外滚子的位置角为φ2,在A′B′上取P点的对应点P′,使∠A′OO2=φ2,P′点与P点是关于∠AOA′的平分线完全对称的,即0P′=OP,a2=a2′,OO1=OO2,图4.9中PO1与P′O2相交在Q点,它们并不共线,因此P′点与P点不具有共同的法线。假设随着P点位置的改变(当然P′点也随着P的改变而改变),使PO1与P′O2在同一条直线上,此时P′与P就有共同的法线,此时:
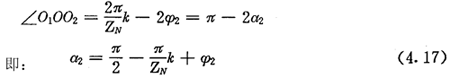
上式就是齿廓AB上与跨槽数为k的齿廓具有公法线的点的条件。当k确定后,若存在公法线,则由(4.17)式并结合基本关系式(2.38)等可解出φ2的值来。
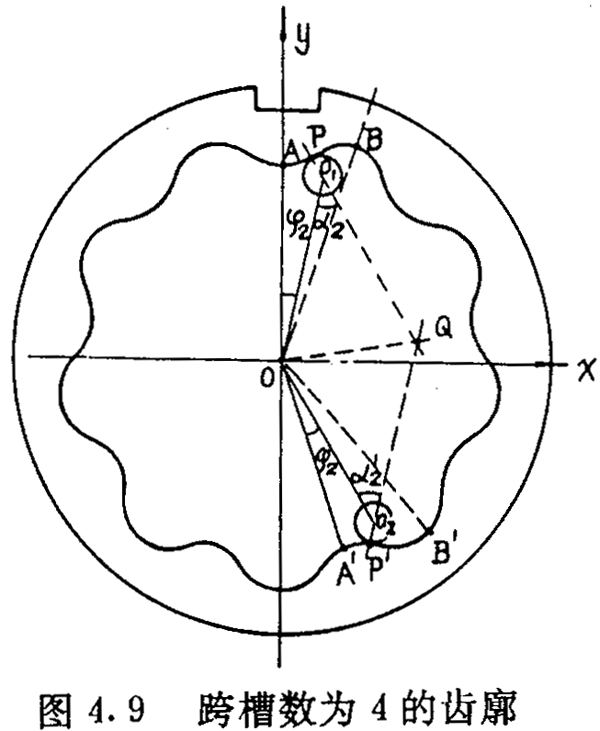
从图4.9可求得公法线长度为:
Wk=2(l1+l)cosa2+2rz (4.18)
式中l1、a2与φ2的关系由基本关系式所确定。显然,两个齿槽的同侧齿廓(同为工作齿廓或非工作齿廓)是不存在公法线的。
4.4.2公法线的数目
由于内齿圈齿廓曲线具有周期性且工作齿廓与非工作齿廓是完全对称的,所以只需讨论一个齿槽的一侧齿廓与其它齿槽的另一侧齿廓所具有的公法线。
令:
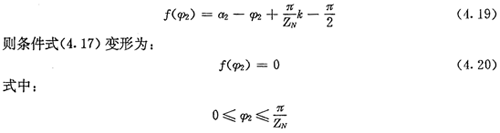
内齿圈的齿数ZN可以是奇数,也可以是偶数(实际产品都是奇数)。为了讨论问题的方便,引用截断取整符号“INT”,当ZN为偶数时, ,当ZN为奇数时,
,当ZN为奇数时, ,由函数式(4.19)可得:
,由函数式(4.19)可得:
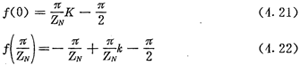
下面就来讲议化跨槽数k取不同数值时,具有的公法线情况:

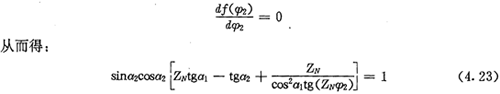





[算例]
对于前面提到的3TWY7.5-12推杆减速器,齿数ZN=11,计算得到k0=4,即当跨槽数k小于等于4时,两齿郭不具有公法线。当跨槽数k=5时,计算得到两条公法线,理论长度分别为:
凸齿公法线 W51=209.632mm,对应于φ2=1.755°
凹齿公法线 W52=215.716mm,对应于φ2=12.485°
当跨槽数k=6时,计算得出只有一条凹齿公法线
W63=230.146mm,对应于φ2=15.205°
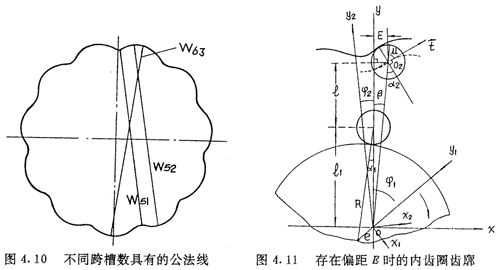
合起来,此推杆减速器的内齿圈齿廓共有三条不同长度的公法线,它们的位置如图4.10所示。
4.4.3刀具轴线有偏距时的内齿廓及公法线
用圆柱形刀具加工内齿圈齿廓时,刀具轴线应在齿圈的半径方向作相对运动,如果它不沿着齿圈半径方向运动,那就有了偏距。在图4.11中,若刀具中心的运动方向平行于y轴,而刀具中心在O2处,那就有了偏距E,现在来分析此时加工出来的齿廓及公法线长度。
同图4.11可得:

利用第二章中推导内外滚子工作角关系的方法可得a2与a1的关系为:
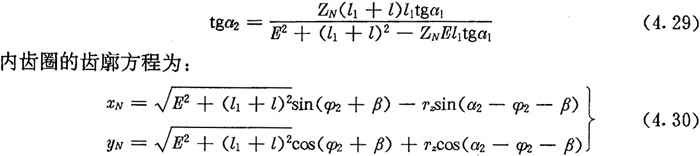
经过分析可知,当存在偏距E时,在跨槽数为k的两齿廓上具有公法线的点的条件仍然可用式(4.17)表示,公法线长度为:
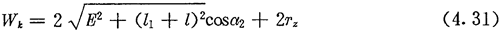
若令(4.30)式和(4.31)式中的E=0,得到的就是无偏距时的内齿圈齿廓理论方程式(2.21)及公法线长度(4.18)式。
4.4.4利用公法线误差分析加工调整参数误差
由齿廓方程式(4.30)可以知道,齿廓形状取决于偏心轴的偏心距e,偏心轴几何中心到固定点长度R,刀具半径Tz,进刀深度l以及刀具轴线偏距E。e和R是夹具结构上的固定尺寸,应该调整得尽量正确,而其误差加△e、△R也是个定值。而△Tz是由于刀具制造误差及加工过程中的磨损引起,△l及△E是由于操作误差引起。因此,△Tz、△l及△E是导致齿形误差的工艺因素。下面来分析它们对公法线长度的影响。
把公法线长度Wk看成是自变量为TZ、l及E的函数,即Wk=Wk(Tz,l,E),由(4.31)式可得:
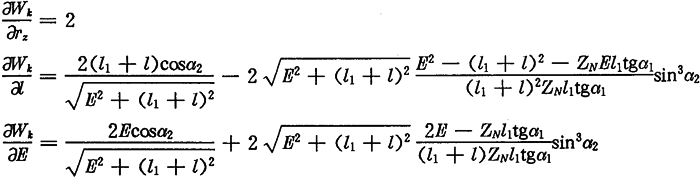
假设用下标i表示公法线序号,用△Wki表示第i条公法线实际测量出的值与理论计算出的值的误差,则可得到公法线长度误差方程为:
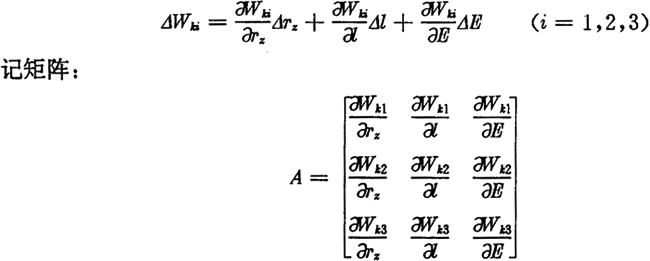
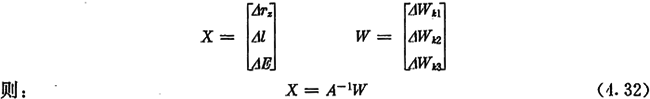
上式中A-1是矩阵A的逆阵,称误差矩阵。当算得相应的偏导数值后,如果测得一个齿槽的一侧齿廓与其它齿廓的三条公法线的误差,代入方程组(4.32)之后,便可求得相应的△Tz、△l和△E。△Tz是经计算得到的刀具半径的误差,△l是进刀深度误差,△E是刀具轴线偏心距的误差,根据计算结果适当调整这些参数就能迅速地提高齿廓精度,使之达到精度要求。
[计算实例]
前面所说的3TWT7.5-12推杆减速器,根据参数可计算得到其误差矩阵A-1为:
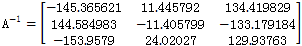
在一个内齿圈齿廓上实际测得三条公法线的长度与理论长度的误差为:
△W51=0.02261mm
△W52=0.03806mm
△W63=0.02106mm
代入式(4.32)可得:
△TZ=0.0202mm,△l=0.032mm,△E=0.1697mm
根据计算结果适当调整这些参数就能迅速提高齿廓精度,使之达到精度要求。
上一页
下一页