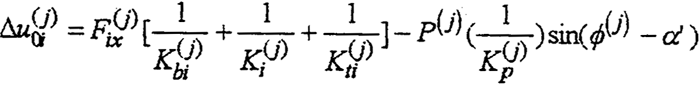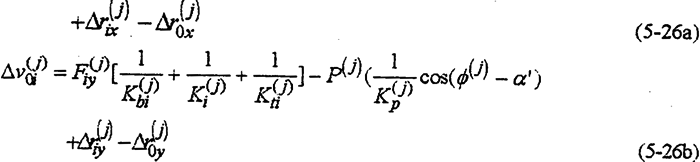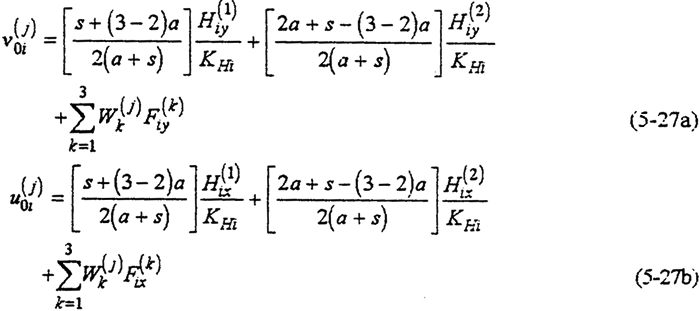式(5-19)中的△u(j)0i,△u(j)0i是啮合接触点p与偏心套中心的距离因机构变形产生的变形增量。它包括齿板啮合接触点与高速轴
孔中心的相对变形量、行星轴承的变形量、偏心套的变形量以及运动副间隙、轮齿齿形误差等。可表示为
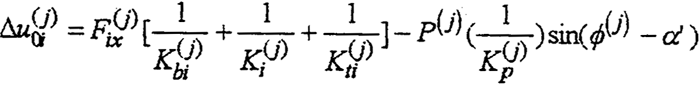
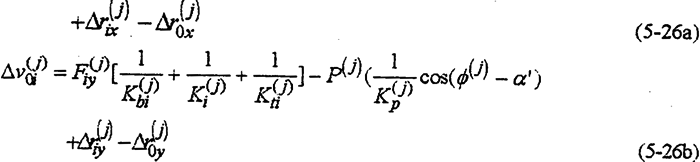
式中
K(j)p是齿圈变形刚度,见表4-2;
r(j)0x,r(j)0y是齿形法向误差在坐标轴方向的分量;
u(j)0i,u(j)0i是高速轴轴心的位移,它是由由箱体轴承变形及轴的弯曲变形引起的,即
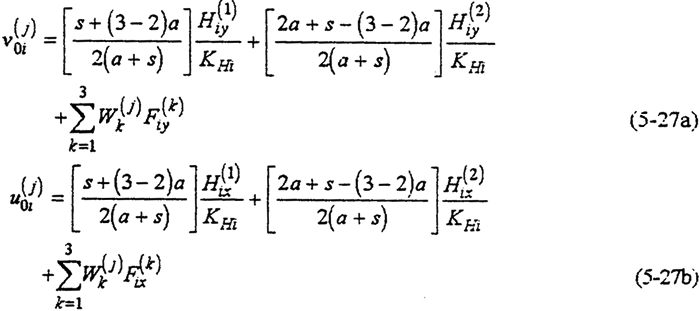
式中W(j)k由(4-63)计算。
表4-2
| φ |
K(108)N/m |
φ |
K(108)N/m |
φ |
K(108)N/m |
| 1.4285 |
2.633 |
121.4285 |
1.592 |
241.4286 |
0.551 |
| 7.1428 |
2.477 |
127.1428 |
1.143 |
247.1428 |
0.676 |
| 12.8571 |
2.280 |
132.8571 |
0.8665 |
252.857 |
0.860 |
| 18.5714 |
2.108 |
138.5714 |
0.6805 |
258.5714 |
1.127 |
| 24.2857 |
2.018 |
144.2857 |
0.5528 |
264.2857 |
1.566 |
| 30.00 |
2.000 |
150.0000 |
0.4625 |
270.0000 |
2.298 |
| 35.7142 |
2.042 |
155.7142 |
0.3980 |
275.7143 |
3.351 |
| 41.4285 |
2.181 |
161.4285 |
0.3512 |
281.4286 |
6.055 |
| 47.1428 |
2.376 |
167.1428 |
0.3168 |
287.1429 |
10.53 |
| 52.8571 |
2.712 |
172.8571 |
0.2926 |
292.8571 |
17.99 |
| 58.5714 |
3.223 |
178.5714 |
0.276 |
298.5714 |
20.41 |
| 64.2857 |
3.994 |
184.2857 |
0.2662 |
304.2857 |
14.656 |
| 69.9999 |
5.407 |
190.0000 |
0.2615 |
310.0000 |
9.91 |
| 75.7142 |
7.808 |
195.7143 |
0.2624 |
315.7143 |
6.526 |
| 81.4285 |
12.62 |
201.4286 |
0.2688 |
321.43 |
4.835 |
| 87.1428 |
18.75 |
207.1428 |
0.27915 |
327.1429 |
3.77 |
| 92.8571 |
19.76 |
212.8571 |
0.2969 |
332.8571 |
3.143 |
| 98.5714 |
12.50 |
218.7714 |
0.322 |
338.5714 |
2.772 |
| 104.2857 |
6.641 |
>224.2857 |
0.358 |
344.2857 |
2.608 |
| 110.0000 |
3.755 |
230.0000 |
0.443 |
350.0000 |
2.565 |
| 115.7142 |
2.356 |
235.714 |
0.466 |
355.77143 |
2.612 |
低速轴轴心位移u(j)00,V(j)00也是由箱体轴承变形及低速轴弯曲变形组成。但由于低速轴的法向尺寸较大、弯曲变形很小,故可忽
略不计,只考虑箱体轴承的变形则有

式(5-27)及式(5-28)中s是两则齿板靠近箱体的距离,a是齿板之间的距离。取箱体轴承的刚度KH0=KHi=1379×105N/mm。偏心套的径向变形△e(j)i以及外齿轮的径向变形△R(j)1均很微小,故一般忽略不计。
高速轴的扭轴变形△β(j)zi由式(4-59)计算。低速轴因径向尺寸比高速轴的远远大,故其变形可忽略不计。
5.4三环减速器的载荷分布
三环减速器的载荷有啮合力、行星轴承载荷以及箱体轴承载荷。其分布情况直接反映出三环减速器的动力学性能。下面分析SHQ40型三环减速器的载荷分布特性。SHQ40的有关参数为
i=20 z1=60 z=63 m=4 e=6.392mm a′=28.10 a=200 T=4000Nm n=1000rmp L1=400mm L2=210mm B=30mm s-55mm d=34mm
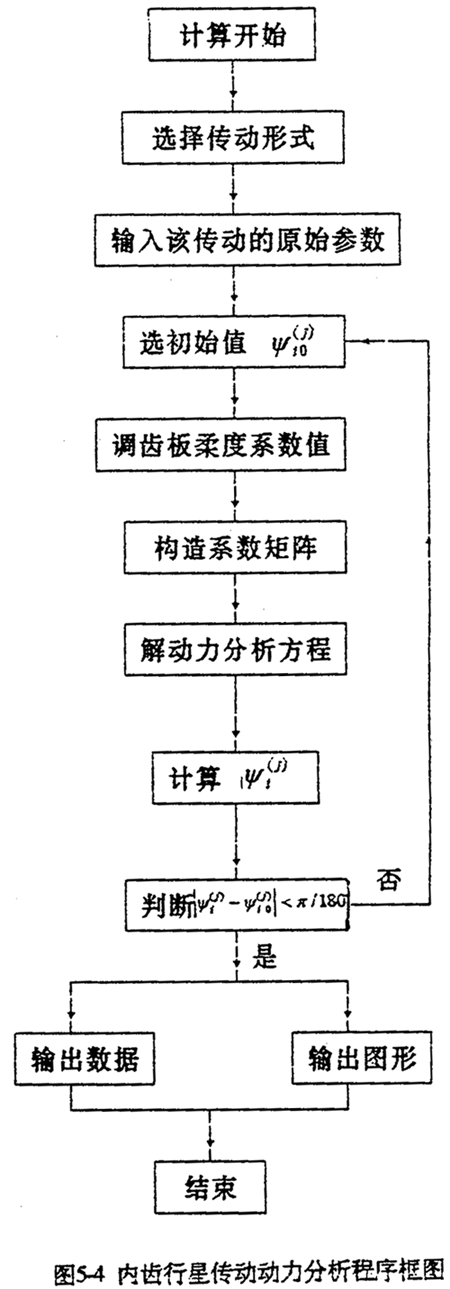
在不计各种误差且机构变形很小时,将以上参数代入三环减速器的非线性动力分析方程式(5-1)~(5-8)、(5-18)、(5-19)、(5-22)~(5-23)等方程,在计算机上求解,就可求得三环减速器各载荷随工况角φ的变化规5-4为计算程图。
5.4.1啮合力分析规律
SHQ40型三环减速器的啮合力随φ的变化规律如图5-5所录。由图可以看出啮合力的以下规律:
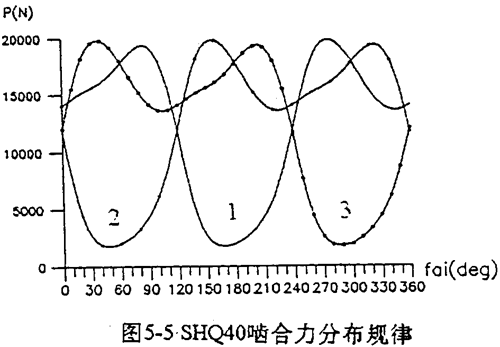
1.三片齿板上对应的啮合图变化规律完全机同,彼此相位差为120°,以360°为击期限变化。
2.无论在什么工况三片齿板的啮合力之和总为常数,但各片齿板的啮合力并不一定相等。即

3.在一个周期内,各齿板的啮合力均各取得两次数值不等的极小值和两次数值相近的极大值。第一片齿板的极值点为

理想情况下,啮合力的极小值在φ=0°、180°产生,极大值在φ=90°、270°产生,造成位置偏离的影响因素主要有轴承刚度,齿板刚度,啮合角以及输入转速、传动比等等。其中轴承刚度的影响极大。在死点的啮合力也产不并一定为零。哈合力可能为负值。为负值时,将阻碍传动的正常转动,产生内齿轮副的干涉现象。并引起减速器冲击振动。因此,按照啮合力过死点时为零的假设分布规律以及啮合力为常数分布规律的模型分析,所得结果都是不可靠的。图5-6是齿板死点位置180°及另一齿板位于超前120°啮合点的单齿啮合图的测试结果。图中每一棒线代表被测齿受啮合力作用一次。比较两图可知,死点位置啮合力总体水平低于120°位置时的啮合力总体水平,与理论分析计算的结果完全吻合。
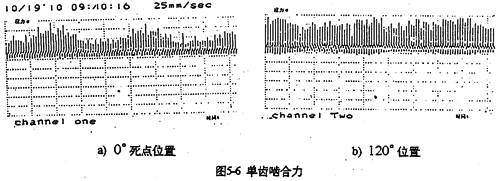
4.将各齿板过死点时的啮合力整理成表,见表5-1所示。
表5-1齿板过死点时的啮合力分布
| 转角φ |
00 |
600 |
1200 |
1800 |
2400 |
3000 |
齿板号 |
第一号 |
第二号 |
第三号 |
第一号 |
第二号 |
第三号 |
死点位置 |
过00死点 |
过1800死点 |
过00死点 |
过1800死点 |
过00死点 |
过1800死点 |
P(1)×104 |
1.4039 |
1.77093 |
1.17171 |
0.20498 |
1.20178 |
1.80810 |
P(2)×104 |
1.17305 |
0.204983 |
1.2009 |
1.80283 |
1.40392 |
1.7759 |
P(3)×104 |
1.20178 |
1.80283 |
1.40614 |
1.77093 |
1.17305 |
0.194746 |
由表看出,各齿板过相同死点位置之不理时的啮合力相等;某片齿板过死点位置时,其它两片齿板超前或者范后干该片啮合120°与水平轴对称。因此,这两片的啮合力相等,从图5-4也反映了这一点,这与实际情况相符合。
5.4.2高速轴行星齿轮减速器中,行星轴承受力大,寿命短,摩擦损耗大,是减速器的薄弱环节。因此,减小轴承载荷,提高行星轴承的寿命,一直是人们力求解决的问题。SHQ40型三环减速器的行星轴承动载荷,提高行星轴承的寿命,一直是们力求解决问题。SHQ40型三环减速器的行星轴承动载荷分布规律,见衅5-7、图5-8、图5-9所示。由图可行出以下结论:
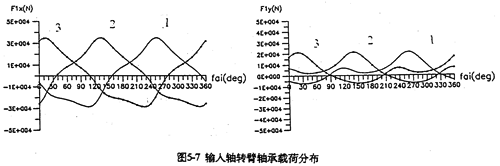
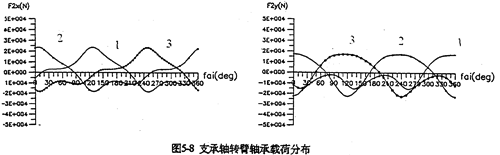
1.三片齿板上对应的行星轴承荷变化情况完全相同,彼此相位差120°,以360°为周期变化。
2.无论是输入轴还是支承轴X方向的行星轴承载荷比y方向的要大,且一周内出现正负两次峰值。这说明行星齿板在水平方向因动载荷产生的振动比垂直方向大。
3.由图5-8可知,支承轴行星轴承在过死点时的y向轴承载荷(切向力)并不为0,说明某相机构在过死点时,是由其它两相机构通过支承从动轴传递扭矩带动该相机构通过死点的。因此,孤立地分析研究一相子机构将偏心套简化为二力杆件建立的模型是不可靠的。
4.输出轴的行星轴承总体载荷比支承轴行星轴承总体载荷大(图5-9),特别是输入轴X方向受力最大。输入轴行星轴承载荷在死点附近取得最小值,在φ=105°、255°取得极大值。极大值产生的位置正好是机构传动角最佳位置附近。在同一时刻,齿板上各输入轴行星轴承的受力状况是不是一样的。当某一齿板接近其死点位置时,轴承载荷较小,而同时另外两片远离死点位置的齿板上输入轴行星轴承载荷要大得多。支承轴的轴承载荷在一个周期内分别出现三次极大值和三次极小的值。由于这个原因使支承轴偏心套的微动磨损比输入轴偏心套的微动磨损更为严重。行星轴承载荷的最大值为
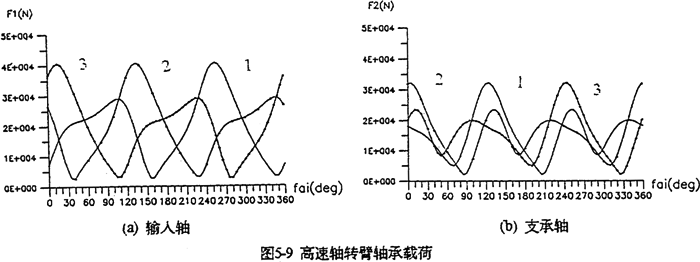
F1max=40662.733713N φ=2550
F2max=32274.64763N φ=1250
根据轴承的寿命计算,三环减速器与K-H-V型少齿差行星减速器相比,K-H-V型的行星轴承当量动载荷约为三环式的1.86倍,而轴承受命,三环式的约为K-H-V型的6.33倍以上。
上一页
下一页