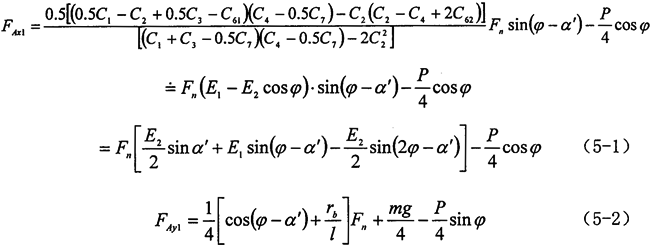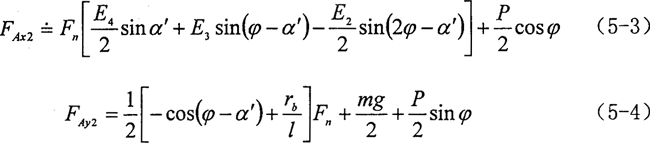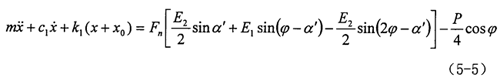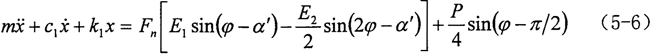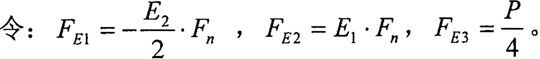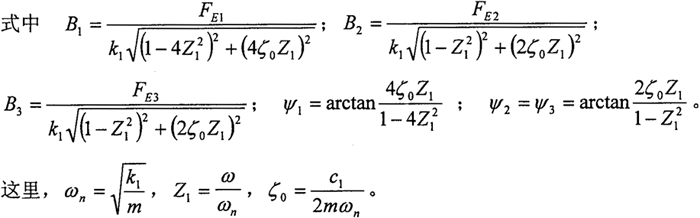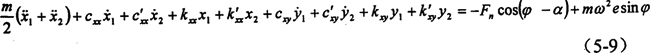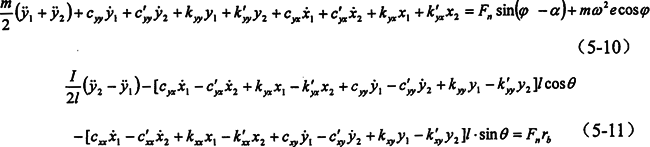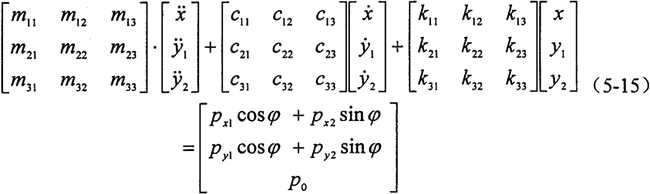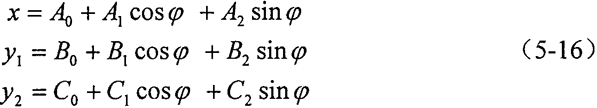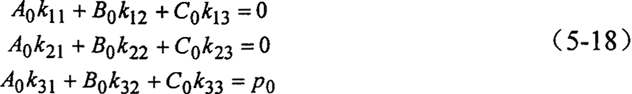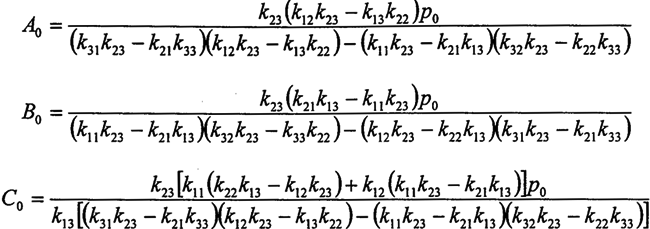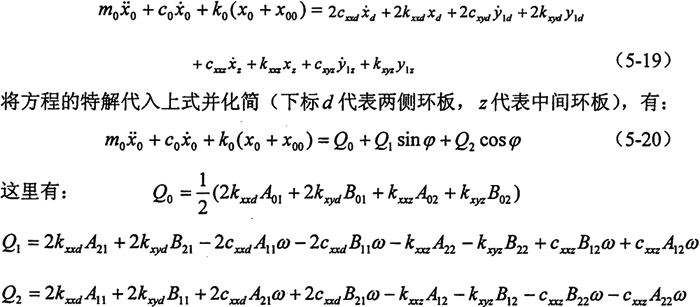第5章 油膜浮动两级三环减速器的振动分析

5.1引言

三环减速器在工作过程中存在较严重的振动，振动的危害很大，影响了这一新型减速装置的推广使用。对三环减速器来说，振动主要是由于环板机构过死点位置时高速轴受到水平方向的双向冲击及垂直向冲击力作用、不平衡惯性力及啮合刚度波动或啮合冲击的的影响。传递功率越大，啮合力也越大，冲击峰越高；转速越高冲击脉宽越小，激振力带宽越宽，这时更容易激发减速器及其附联结构的广泛共振，从而发生强烈振动。文献采用红外热成像技术对三环减速器温升问题进行了测试和分析也证明轴承是主要的发热源，三环减速器的振动和温升均源于输入轴的恶劣承载工况，特别是过大的死点冲击。

笔者设计的新型三环减速器的均载装置就是利用了滑动轴承的动压原理，在三环减速器输入轴偏心套与环板轴承内圈之间插入一个能够自由转动的浮动套筒（浮环），在偏心轴旋转时，在偏心套与浮环之间、浮环与轴承内圈均形成动压油膜，这种结构减小了偏心套与轴承内圈、偏心套与输入轴的刚性接触，提高了偏心套、环板轴承的寿命。当一块环板的转臂轴承所受的载荷增加时，相应的偏位角随之减少，这降低了接触面的温升，更重要的是浮环内、外所形成的油膜的最小油膜位置的点将产生移动，使内啮合放松，啮合力减小，则该环板上的载荷自然就会减少，同时，另外一环板，则使内啮合变紧，啮合力增大，环板上的载荷自然就会增大，从而达到各环板载荷均衡的目的。

本文提出的新型三环减速器以同步带传动作为一级传动实现高速轴的同步输入，克服了高速轴受到水平方向的双向冲击力作用，对整机来说其不平衡惯性力（力矩）为零，同时，均载后各环板单位宽度的啮合力基本相等，使得啮合力峰值下降。同时，两级三环减速器减振的原因还有：

1.采用油膜浮动后，两侧环板理论上同步，理论和实验也证明，新型三环减速器的载荷不均匀系数较现有的环板偏心相位差为120°的减速器的小，因而，降低了冲击力的幅值，使振动减弱。

2.偏心相位差为180°的新型三环减速器增加了一级同步带传动，带的弹性及双轴同步输入使得减速器受力合理，产生的冲击变小，振动减小。

3.采用一级传动后，作为二级传动三环传动的输入转速减小，二级传动中单片环板所产生的惯性力和惯性力矩较原三环减速器的要小的多，环板作用在高速轴上的惯性力自然下降，同时，新型减速器整机的惯性力和惯性力矩为零，使得惯性力（力矩）引起的振动减弱。

本章将对油膜浮动新型两级三环减速器的减振机理和振动问题进行研究。

5.2 油膜浮动两级三环减速器的减振机理

振动将降低三环减速器的承载能力和寿命，同时，还产生噪声，恶化环境，三环减速器的环板机构在过死点时将受到较大的死点冲击，这是三环减速器振动较大的主要原因，各环板的载荷分配不均又加剧了振动。三环减速器有两高速偏心轴和通过转臂轴承安装在高速轴上的三片内齿环板，工作时产生的惯性力和惯性力矩也是引起振动的一个重要因素。振动和发热问题都与啮合力的大小成正比，本文提出的新型油膜浮动均载完全平衡两级三环减速器，其同步带传动能够克服高速轴受到的水平方向的双向冲击力作用，并使得原减速器上作用的周期性的啮合力转变为新型减速器的恒定啮合力，同时，三环传动的转速降低，使得作用在偏心转臂轴承处的惯性力降低，也使得冲击脉宽越大，激振力带宽变窄，这时不容易激发减速器及其附联结构的广泛共振；完全平衡的环板布置方案能够使惯性力（力矩）完全平衡，更重要的是使得啮合力产生的作用到偏心轴支撑轴承的作用力变小；而在偏心轴和转臂轴承之间加装油膜浮动装置，这相当于环板和偏心轴之间采用了弹性连接，既可有效的实现三环减速器的均载，又可减轻三环传动的振动。下面予以讨论。

下面以一块环板为例分析油膜浮动的减振原理。

对于原三环减速器，环板相当于支撑在刚度为K的偏心套上，如图5-1所示，输入端结构如图5-2所示。

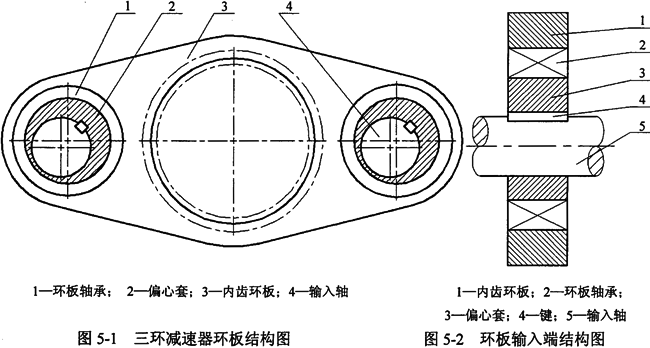
由第二章的内齿环板受力知，作用在转臂轴承处的作用力（以A₁点为例，且将环环示为等效的等截面杆）可表示为：

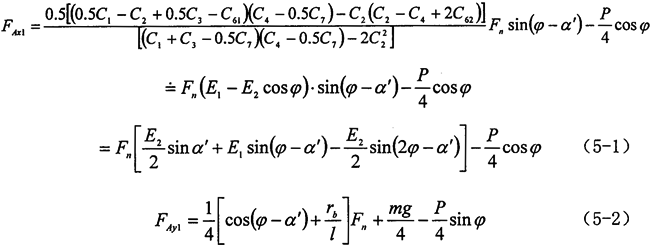
同理，可得到A₂的受力方程，A₃的受力方程与A₁的相同。

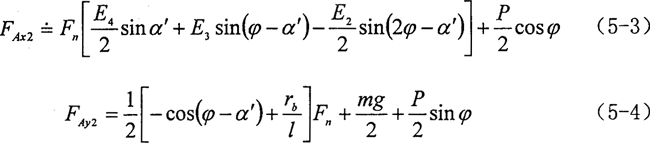
式中的E₁、E₂、E₃和E₄均为与结构有关的常系数。

由上面受力表达式可看出，双轴输入式三环减速器转壁轴承处的水平方向的激振力较垂直方向的激振力要复杂的多，但均为简谐激励函数的和。而对于一般三环减速器，由于啮合力也为复杂的函数，且峰值啮合力为双轴输入时啮合力的两部，同时，由于输入转速度，其惯性力的幅值也较双轴输入式三环减速器大的多。

对于新型三环减速器，分别c和y坐标方向来研究（以A₁点为例），由牛顿定律可列出转臂轴承的运动微分方程。

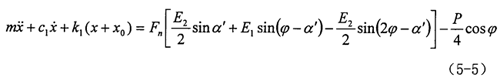
式中 m——转臂轴承质量；c₁——油膜阻尼系数；k₁——油膜刚度。

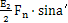是常数项，只对系统地静变形的位置有影响，而不会对系统在静平衡位置近旁振动的规律产生影响，因此，该项产生的自由衰减运动渐渐消失。

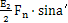=k₁x₀

所以，式（5-5）可用下式表示：

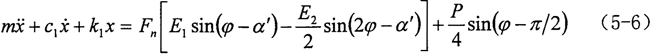
这是复杂周期性激励引起的受迫振动方程。根据叠加原理，线性系统在激振力F（x）作用下的响应，等于其各次谐波单独作用响应的总和。

由振动理论知，单自由度系统在简谐激振力作用下的强迫振动的解由以固有频率ω_n为频率的通解和以ω为频率的特解组成，由于阻尼的存在，以固有频率ω_n为频率的运动将趋于消失，这里只考虑其特解。

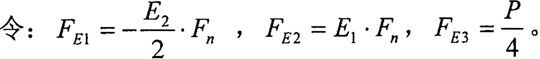
对式（5-6）求解，得系统的位移响应：

x=B₁·sin(2ωt-α′+ψ₁)+B₂·sin(ωt-α′+ψ₂)+B₃·sin(ωt-π/2+ψ₃)               (5-7)

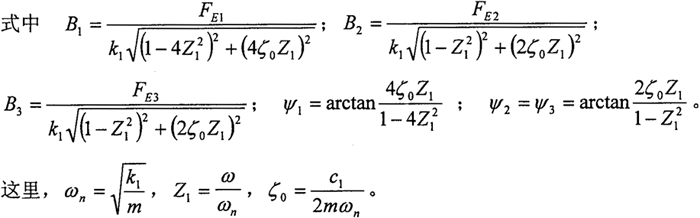
将有关参数代入上式便可获得系统的位移响应曲线。

对系统的位移响应（5-7）式求导，有：

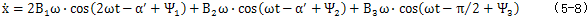
对系统的速度响应（5-8）式求导，有：

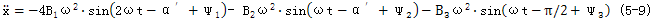
对于与x坐标轴方向相垂直的y方向，也可仿上面过程进行推导，但由于其激振力不含2φ项其结果比x坐标轴方向要简单一些。

实际上，减速器的振动主要表现为偏心轴支撑轴承的振动，其振动的主要激振力便是转臂轴承处的油膜作用力和偏心轴的惯性力和惯性力，偏心轴的惯性力和惯性力矩对支撑的作用力为零，由第二章受力分析知，双轴输入式三环减速器支撑轴承所受的x方向激振力为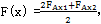：对比（5-1）和（5-3）式可看出，惯性力项抵消，而且F_Ax1、F_Ax3与F_Ax2的作用力方向相反，因而，笔者设计的油膜浮动两级三环减速器较一般的三环减速器在支撑轴承处的振动要小的多。

综上，油膜浮动两级三环减速器的减振机理：

1.完全平衡使得环板和偏心轴的惯性力及惯性力矩对偏心轴和输出轴支撑轴承的激振力为零，消除了惯性力及惯性力矩在偏心轴和输出轴支撑轴承处产生的振动。

2.同步带实现了双偏心曲柄轴同步输入，使得三环减速器的啮合力为定值，且对输出轴支撑轴承的激振力理论上为零，对偏心轴支撑轴承的激振力也减小，啮合力所产生的振动减小。

3.油膜浮动均载使得任一环板的实际的单位宽度上的啮合力的最大值降低，从而减小了啮合产生冲击力的幅值，这样，振动自然也减少。

4.油膜浮动均载时由于祸合的影响以及油膜的吸振功能，也使得减速器的振动减少。

5.一级同步带传动，降低了偏心轴的转速，因而除减小了惯性力和惯性力矩的影响外，还使得激振力带宽变窄，使得激发减速器及其附联结构的广泛共振的可能性减小。

5.3油膜浮动均载的两级三环减速器的振动分析

由第三章的分析知，油膜力是复杂的非周期性函数，考虑到轴径的振幅很小，对油膜力作线性化处理（所得函数仍含有耦合项），由于油膜刚度较转臂轴承和偏心轴的刚度小的多，这里仅考虑油膜的影响，应用牛顿第二定律可列出该环板的运动微分方程（先不考虑环板的标号）。

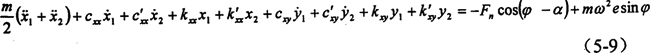
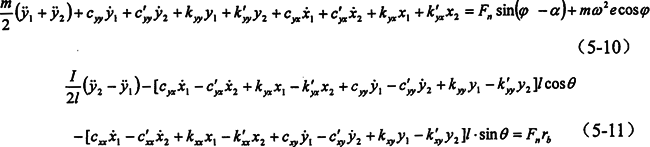
由上面三个公式可看出，即使作了线性化处理，公式中仍然含有耦合项，即k_xy、k_yx、c_xy和c_yx一般不等于零，油膜正是这些特性的影响下具有良好的吸振能力。

由于方程数比未知数少一个，需补充一个方程。根据环板长度不变的条件，

式中 c_xx、c_xy、c_yx、c_yy、c_xx′、c_xy′、c_yx′、c_yy′——环板左、右支撑的油膜阻尼系数；

k_xx、k_xy、k_yx、k_yy、k_xx′、k_xy′、k_yx′、k_yy′——环板左、右支撑的油膜刚度系数。

这些系数可通过实验测定。

（5-13）式可写成：

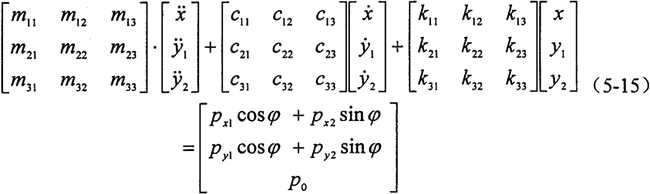
设方程的特解为（不考虑环板的编号）：

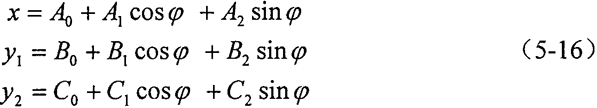
代入方程求解有：

A₁（k₁₁-m₁₁ω²)+A₂c₁₁ω+B₁k₁₂+B₂c₁₂ω+C₁k₁₃+C₂c₁₃ω=p_x1

A₁(-c₁₁ω)+A₂(k₁₁-m₁₁ω²)+B₁(-c₁₂ω)+B₂k₁₂+C₁c₁₃ω+C₂k₁₃=p_x2

A₁k₂₁+A₂c₂₁ω+B₁(k₂₂-m₂₂ω²)+B₂c₂₂ω+C₁(k₂₃-m₂₃ω²)+C₂c₂₃ω=p_y1

A₁(-c₂₁ω)+A₂k₂₁+B₁(-c₂₂ω)+B₂(k₂₂-m₂₂ω²)+C₁(-c₂₃ω)+C₂(k₂₃-m₂₃ω²)=p_y2

A₁k₃₁+A₂c₃₁ω+B₁(k₃₂-m₃₂ω²)+B₂c₃₂ω+C₁(k₃₃-m₃₃ω²)+C₂c₃₃ω=0

A₁(-c₃₁ω)+A₂k₃₂+B₁(-c₃₂ω)+B₂(k₃₂-m₃₂ω²)+C₁(-c₃₃ω)+C₂(k₃₃-m₃₃ω²)=0

写成矩阵形式：

[N]_6×6[A]_6×1=[P_N]_6×1                         (5-17)

式中 [A]=[A₁ A₂ B₁ B₂ C₁ C₂]^T是一个6阶线性代数方程组，其行列式不等于零，根据文献的主元素消去法编写的简单的数值计算程序便可方便的求得。

[A]_6×1=[N]^-1_6×6[P_N]_6×1

特解中的常数项构成的方程组为：

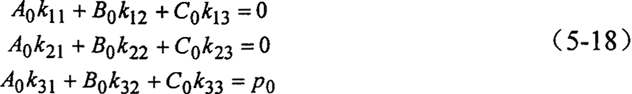
这是一个3阶线性代数方程组，其行列式不等于零，对上式求解有：

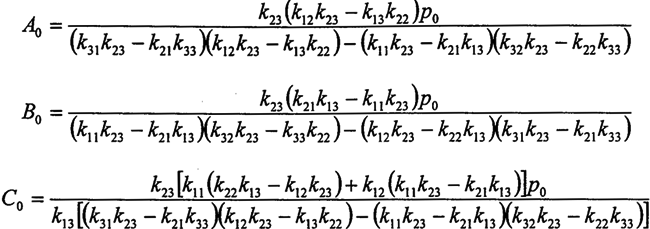
这样，方程的特解便得到，通过油膜作用在任一环板支撑的力的表达式也就确定了。各环板作用在两偏心轴的力上也随之得到。

对新型油膜浮动三环减速器的曲柄轴轴承支撑，可用振动理论进行分析。

下面讨论油膜力对曲柄轴的影响。由于是对称布置，中间环板为单侧环板质量的2倍且成180°相位差，其惯性力（力矩）完全平衡，不计其影响。应用牛顿第二定律可列出曲柄轴的运动微分方程（以左支撑的x轴为例）：

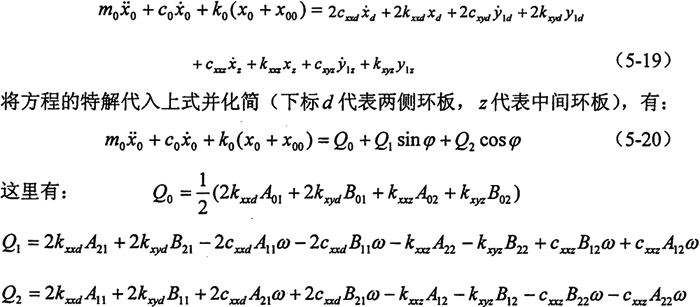
式中 m₀——偏心轴的质量的一半；c₀——左支撑轴承的阻尼；

k₀——左支撑轴承的刚度。

k₀x₀₀=Q₀，此为振动的平衡位置。

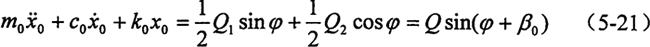
这个方程的瞬态解为：

x₀=H₀e^-αtsin(ω_nt+θ₀)+H₁sin(ωt+β₀-ψ)                              (5-22)

由Q₁和Q₂的表达式可以看出，两侧环板与中间环板通过油膜对高速轴的作用方向相反，互相抵消，即Q₁和Q₂较小，Q也较小；又由于油膜的刚度小于转臂轴承的刚度，Q₀也减小。

(5-22）式表明，环板的振动是以ω_n和ω。为频率的两种振动的组合，其中以ω_n为频率的振动经过一段时间后将消失。

则方程的稳态解为：

x₀=H₁·sin（ωt+β₀-ψ）                          （5-23）

对于与x坐标轴方向相垂直的y方向，也可仿上面过程进行推导，其结果与x坐标轴方向结论一致。另一高速轴也有一致的结论。由于实验条件和时间所限，油膜的动特性系数尚未确定，故本文未给出数值解。但这不影响本文的分析和结论。

在样机参数下，挤压油膜刚度较小。三环减速器油膜浮动主要就是利用流体阻尼，来耗散振动体的振动能量，达到减小振动的目的。

5.4本章小结

本章在三环减速器受力分析和油膜浮动研究的基础上，对油膜浮动均载两级三环减速器的振动性能进行了系统研究。

分析表明：振动产生的主要原因在于高速轴受到的双向冲击、啮合力波动以及惯性力（力矩）的作用，消除或减小这些因素的影响是笔者设计的主要目的。结合新型三环减速器样机的振动分析，对油膜浮动两级三环减速器的减振机理进行了研究，这为设计振动性能较好的三环减速器提供了理论依据。依据振动理论、变形协调条件以及流体动力润滑理论，对油膜浮动两级三环减速器的振动性能进行了研究，推导出了油膜浮动条件下转臂轴承处和曲柄轴支撑轴承处的动态响应方程，揭示了油膜浮动均载装置的减振原因。总的来说，油膜浮动两级三环减速器有着良好的减振性能。

上一页

下一页