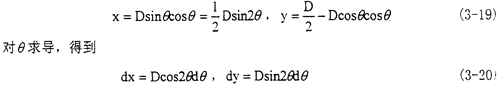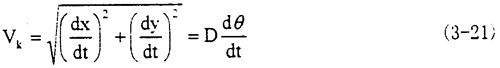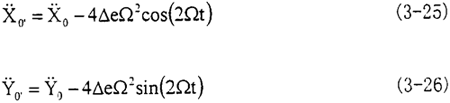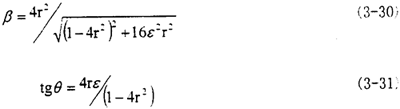3.4 不对中时的运动及动态特性
实际上可以将不对中分为冷态不对中和热态不对中两种情况。其中冷态不对中主要是指在室温下由于安装误差造成的对中不良；热态不对中指联轴器在运行过程中由于温度等因素造成的不对中。其主要原因有：转子各零部件受热不均，使联轴器产生热膨胀变形和扭曲变形；发动机热膨胀时由于表面的摩擦力及导向键磨损引起轴承座倾斜和侧行；由于转子的饶性和重量分配不均匀，转子在安装之后产生原始弯曲，进而影响对中情况。
3.4.1 不对中时的运动分析
（1）当转子轴线存在轴向的位移时（如图3.2），轴向位移只会产生附加的周向应力，而不会影响转子的运动特性。所以这里不进行计算。
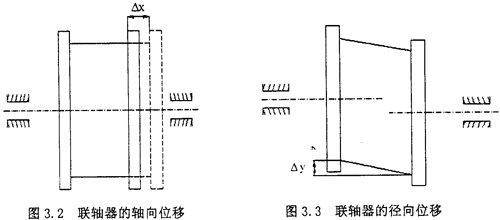
（2）当转子轴线之间存在径向位移时（如图3.3所示），联轴器的中间套齿与半联轴器组成移动副，不能相对转动，但是中间套齿与半联轴器产生相对滑动而作平面圆周运动，即中间套齿的中心是沿着以径向位移△y为直径作圆周运动，如图3.4所示。
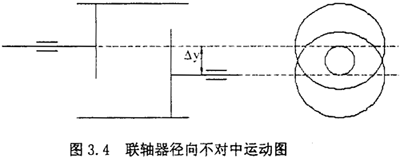
设A为主动转子的轴心投影，B为从动转子的轴心投影，K为中心齿套的轴心，那么有AK丄BK，设AB长度为D，K点的坐标为K（x，y），取θ为自变量，如图3.5所示。则有
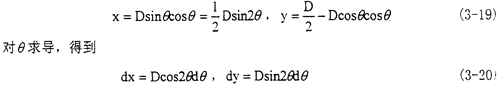
则K的线速度为
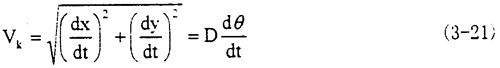
由于中间套齿平面运动的角速度等于转轴的角速度，即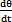
=ω，所以K点绕圆周中心运动的速度为
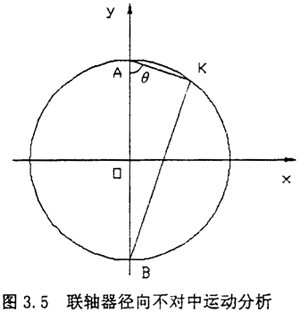
由上式可知，K点的转动为转子转动的角速度的两倍，因此当转子高速运动时，就会产生很大的离心力，激励转子产生径向振动，其振动频率为转子工频的两倍。
（3）当转子轴线之间存在偏角位移时（如图3.6），从动转子的角速度与主动转子角速度是不同的，从动转子的角速度为
式中 ω1，ω2——分别为主动转子和从动转子的角速度
α——从动转子的偏斜角
ф1——主动转子的转角
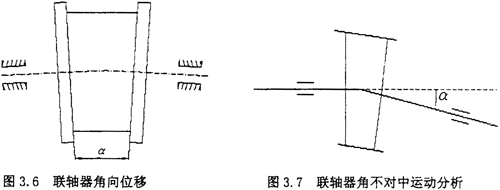
当主动转子的回转角速度为常数时，从动转子的角速度是偏角和主动转子转角的函数。当或ф1=00或1800时，ω2最大，当ф2=900获2700时，ω2最小。其转速比变化曲线如图3.8所示，即有ω1cosa≤ω2≤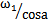
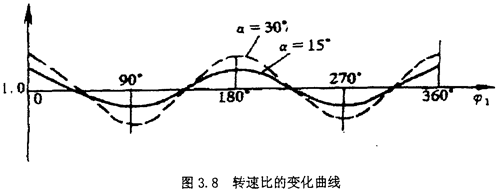
由此可知，当发动机或机组的转子轴线发生偏角位移时，其传动比不仅随转子每转一周变动两次，而且其变动的幅度虽偏角的增加而增大，因而从动转子由于传动比变化所产生的角加速度激励转子而发生振动，其径向振动频率也为转子工频的两倍。
(4）实际旋转机械的转子联轴器处既有平行不对中，又有偏角不对中，即为两种情况的综合，因而转子发生径向振动的频谱特征是两者综合的结果，其径向振动频率为转子工频的两倍。
3.4.2 不对中时的动态特性
由上面的运动分析可知，轴向不对中时对联轴器的运动情况可以忽略。所以动态特性分析也只考虑平行不对中、偏角不对中以及平行偏角不对中三种情况。
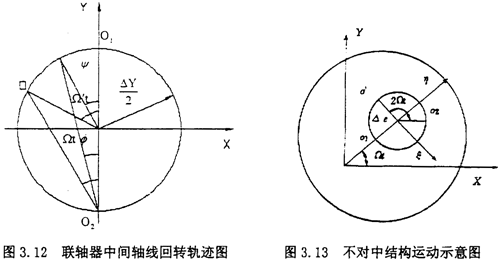
联轴器连接的两转子轴线之间发生不对中故障时具有平行位移或角度位移，在运动传递过程中，联轴器中间齿套的运动必须同时满足两半联轴器的需要，即中间齿套轴线作平面运动，且轴心线的回转运动频率与转子的运行频率不一致。当产生平行不对中、偏角不对中和平行偏角不对中三种情况时，联轴器中间齿套的轴线回转轨迹分别为图下图所示的圆柱体、双锥体和半双锥体。在这些图中，O1，O2为两半联轴器的轴心，O，O′为联轴器中间套齿的静态和动态回转中心，△y，△α分别为转子系统的平行和偏角不对中量。
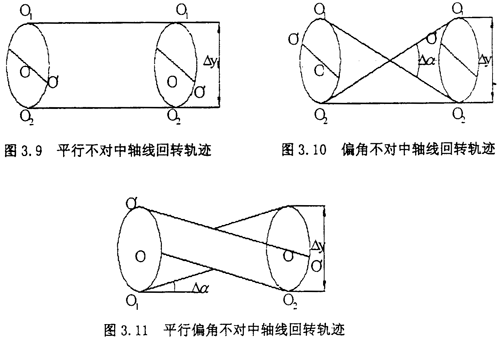
对于上面图中所示的三种情况，任意回转轮廓的截面图为一周，如图3.12所示，O′的运动轨迹可以描述为
X=△Esin（Ω′t-Ψ） （3-24）
式中 Ω——转子的回转角频率
△E——当量不对中量，△E=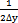
（平行不对中时）；
△E=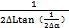
（偏角不对中时）
Ψ——初始相位角，Ψ=2ф（平行不对中时）；
Ψ=2ф（偏角不对中时左端）；Ψ=2ф-
（偏角不对中时右端）
中间套齿对转子系统施加的激振力为
Fx=4M△EΩ2sin（Ωt-ф），Fy=4M△EΩ2cos2（Ωt-ф） （3-24）
工作状态下联轴器的动态特性如图3.13所示，两半联轴器的中心为O1和O2，联轴器外壳的动态中心为O′，当系统以Ω转动时，外壳重心的加速度在
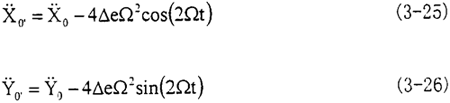
其中△e=OO′为系统当量不对中量，在转轴的弹性力的作用下，由质心运动定理：m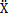
0=-kX，m
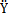0-kY，考虑到外阻力的作用
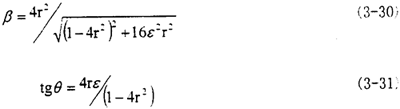
现在对结果进行讨论：
(1）当r趋近于O时，动力放大系数M趋近于O；θ趋近于O，这表明，系统在转速较低时，其向应振幅较小，且有较小的相位角。
(2）当r=1/2时，系统发生共振，系统具有振幅最大值，该值的大小只与阻尼系数有关，与此同时，相位角为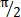
。
(3）当r趋近于∞时，动力放大系数M趋近去1，这表明，系统在转速较高时，其向应振幅趋于稳定。振幅并不随激振力的迅速增加而加大，与此同时，相位角θ趋近于π，并逐渐保持稳定。
3.5 本章小结
本章通过引入联轴器的刚度和阻尼，计算了弹性联轴器在周期性载荷与冲击载荷下的动力特性。在第四节中着重分析了平行不对中，偏角不对中以及平行偏角不对中的运动与动力特性。
从各种不对中的运动学和动力学分析可以得出如下结论：
(1）激励力幅与不对中量成正比，随不对中量的增加，激励力幅则线性加大
(2）在不对中情况下，中间圆环的轴芯线相对于联轴器的轴心线产生相对运动，其中，平行不对中的回转轮廓为一圆柱体，偏角不对中时为一双锥体，平行偏角不对中时为半双锥体。回转体的范围由不对中量决定。
(3）联轴器处于工作状态时，无论是哪一种不对中形式，系统的响应在转速达到临界转速的一半时发生共振，振幅具有最大值。同时，相位角为。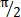
(4）系统在转速大于临界转速后，随转速的增加，其响应振幅趋于稳定，并不随激励力的迅速增加而增大。
上一页
下一页
