第4章 不对中状态的理论分析
4.1 以材料力学为基础的受扭分析
联轴器正常工作情况下，只受到一个旋转的扭矩。因此首先来研究圆环受扭转时的应力，这要综合研究几何、物理和静力等三方面的关系。
4.1.1 变形几何关系
为了观察圆轴的扭转变形，与薄璧圆筒受扭一样，在圆周表面上作圆周线和纵向线，在扭转力偶矩m作用下，得到与薄璧圆筒受扭时相似的现象。即：各圆周线绕轴线相对地旋转了一个角度，但大小，形状和相邻圆周线的距离不变，在校变形的情况下，纵向线仍然近似地是一条直线。只是倾斜了一个微小的角度，变形前表面上的方格，变形后错动成菱形。
根据观察到的现象，做下述基本假设：圆周扭转变形前原为平面的横截面，变形后仍保持平面，形状和大小不变，半径仍保持为直线；且相邻两截面间的距离不变。这就是圆周扭转的平面假设。按照这一假设，扭转变形中，圆轴的横截面就像刚性平面一样，绕轴线旋转了个角度。以平面假设为基础到处的应力和变形计算公式，符合试验结果，且与弹性力学一致。
在图4.1中，ф表示圆周两端截面的相对转角，称为扭转角。扭转角用弧度来度量。用相邻的横截面p-p和q-q从轴中取出长为dx的微段。剪应变
y=P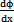
（4-1）
式中dф／dx是转角φ沿x轴的变化率。对一个给定的截面来说，它是常量。公式表明，横截面上任一点的剪应变与该点到圆心的距离p成正比。
4.1.2 物理关系
以
P表示横截面上距圆心为ρ出的剪应力，由剪切胡克定律知道
P=G·y （4-2）
将式（5-1）代入上式则可以得到
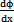P= G·P （4-3）
这表明，横截面上任一点的剪应力ρ与该点到原新的距离ρ成正比。因为Yρ发生于垂直于半径的平面内，所以Yρ也与半径垂直。如果注意到剪应力互等定理，则在纵向截面和横截面上，沿半径剪应力的分布如图4.2所示
因为公式中的 dф／dx尚未求出，所以仍不能用它计算剪应力，这就要用静力关系来解决。
4.1.3 静力关系
于圆轴横截面内，按极坐标取微分面积dA，求出内力系对圆心的力矩就是截面上的扭矩即：
Ip称为横截面对圆心点的极惯性矩。由公式可以算出横截面上距圆心为ρ的任一点的剪应力为：
在圆截面边缘上，ρ为最大值R，得到最大剪应力为：
引用记号Wt=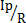
，Wt为抗扭截面系数，便可以改写公式为τmox=
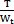，导出的公式中引进了截面极惯性矩和抗扭截面系数，在空心轴的情况下有
其中D和d分别为空心圆截面的外径和内径，R为外半径，α=d/D
最后建立圆轴扭转的强度条件，根据轴的受力情况或扭矩图，求出最大扭矩Tmax。对于等截面杆，按照公式算出最大剪应力τmax不超过许用应力[τ]，
4.2 以弹塑性力学为基础的受扭分析
在材料力学中已知圆轴扭转时的变形规律。随着扭矩MT的增加，剪应力也不断增大。由于圆轴最外层剪应力最大，因而最外层首先进入塑性状态，此时的扭矩就是圆轴的弹性极限扭矩
MT=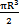
（τθz）max （4-11）
（1）当最外层开始屈服时，此时最外层剪应力应达到剪切屈服应力τy，即（τθz）max=τy，如图4.4（a），于是有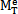
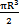=τy。
若选用Mises屈服准则，则有
若选用Tresca屈服准则，则有
（2）当圆轴整个截面都进入塑性状态，如图4.4（c），此时的扭矩就是圆轴的塑性极限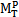
，即
若选用Mises屈服准则，则
若选用Tresca屈服准则，则
（3）当扭矩MT处于弹性与塑性极限扭矩之间时，即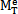<MT<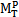时，则圆轴外层处于塑性状态，内层处于弹性状态，弹性区与塑性区的分界面半径为rP,此时扭矩
此时剪应力在截面上沿半径R的分布情况见如图4.4（b）所示。
若先Mises屈服准则，则有
若选用Tresca屈服准则，则有
随着扭矩的增加，塑性区由圆轴的外层向轴的中心逐渐扩大，直至整个截面全部进入塑性状态。当轴的整个截面全部进入塑性状态后，圆轴将进入无约束的塑性变形，此时的圆轴将完全丧失承载能力。
弹性与塑性极限扭矩之比为：
4.3 轴向不对中时的联轴器的工作状态
在像胶右端面圆环上取单元体，且在分析过程中时取关键的四个象限点的位置作为研究对象，分别为90°，180°，270°，360°位置为研究对象。后面的径向不对中、角向不对中以及综合不对中也采用相同的4个位置进行分析。
轴向不对中时，由于轴向的偏移，橡胶圆环左端面受到附加的向左拉应力，右端面则受到附加的向右的拉应力，并且在旋转过程中，拉应力σax的大小和方向的大小和方向都不会随着圆环的旋转角度改变而改变；由橡胶圆环旋转扭矩产生的剪应力τrot方向始终与其线速度方向相反，而线速度方向在旋转一周的过程中不断的变化。轴向不对中时的应力情况应该是σox与τrot的叠加，所以其受力情况比较复杂。
根据实际情况计算出工作时的剪应力：GK2型内燃机车启动发电机ZQF-38TH,115V,38KW,1170～358Or/min；GK2型内燃机机用柴油机型号为MTU16V396TC14，持续功率为1378KW，旋转角速度为18O0rad/min。柴油机冷区液温度为40℃时最小启动转矩包括加速余量约8OON.m，曲轴扭矩约75ON.m
根据联轴器破坏时的橡胶圆环的裂纹方向和角度，可以知道裂纹有一个400的斜角，也就是说引起破坏的应力平面具有一定的角度。首先假设破坏仅仅是源于轴向不对中应起的，下面对具体的位置进行讨论。
（1）轴向不对中90°位置：当圆环上的单元体旋转到最上方时，也就是90°位置时，单元体的应力如下图所示。
此时的受力情况其实属于二向应力状态，利用解析法可知
最大主应力平面如图4.9所示。
上一页
下一页
