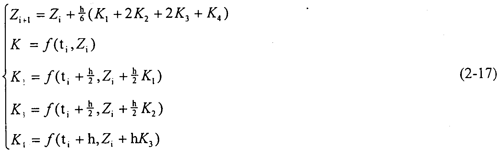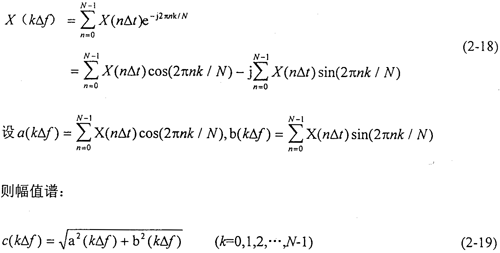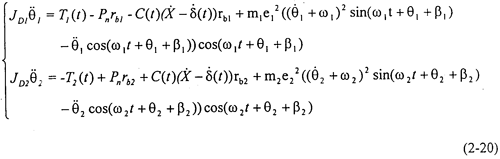2.3.1 方程数值解法
采用经典的四阶Runge-Kutta法或四阶的Runge-Kutta-Gill法求方程组的数值解,即可求得齿轮的扭转振动时程响应。为了保证求解收敛,求解过程中应采用变步长迭代。其计算公式如下:
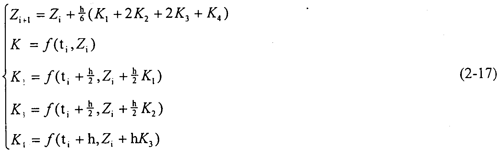
1.迭代初始值的选取:
有三种方式:
(1)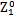 =
= =
=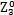 =
=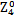 =0,即
=0,即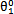 =
=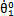 =
=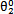 =
=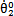 =0
=0
这种取值方法对求瞬态应较为有利,但计算时间较长时也可求得稳态响应;
(2)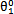 和
和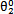 的值根据额定扭矩下求得齿轮扭转角,
的值根据额定扭矩下求得齿轮扭转角,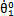 和
和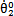 =0的值取额定旋转角速度,迭代时间很长才能求得稳态响应;
=0的值取额定旋转角速度,迭代时间很长才能求得稳态响应;
(3)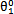 和
和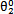 的值根据额定扭矩下求得齿轮扭转角,
的值根据额定扭矩下求得齿轮扭转角,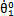 和
和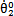 =0,这种方法可在较短的时间内求得稳态响应。
=0,这种方法可在较短的时间内求得稳态响应。
2.幅值谱计算
在求得了齿轮的时程响应后,经过FFT变换可求得齿轮相对振动的幅值谱。幅值谱计算公式:
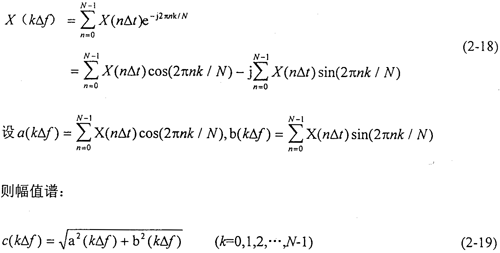
3.数值算例
以直齿圆柱齿轮为例(斜齿圆柱齿轮应把齿数Z换成当量齿数ZV),计算齿轮齿侧间隙变化对齿轮振动故障频率成份的影响以及齿轮工作载荷及转速的对齿轮振动故障频率成份的影响。取零初始条件计算。
4.齿轮具体参数如下:
模数 m=3mm
齿数 Z1=23,Z2=45
分度圆半径 r1=34.5mm,r2=67.5mm
基圆半径 rb1=32.4mm,rb2=63.4mm
扭矩 T1=63.47Nm,T2=124.57Nm
重合度 ε=1.677
齿宽 b=20mm
啮合刚度谐波项: K0=5.6157×108N/m,K1=1.8107×108N/m,K2=0.9558×108 N/m,
K3=0.0691×108 N/m
齿轮当量质量 m1=0.293kg, m2=1.216kg
阻尼系数 C=3275
齿轮转动惯量 JD1=0.000307945kgm2,JD2=0.004888484kgm2
电动机转速 n=960rpm
齿侧间隙 0~0.3mm
2.3.2 考虑齿轮齿侧间隙的振动频谱特征
轴承对箱体动态激励力和齿轮相对振动位移X=(rb1tgθ1-rb2tgθ2)有相对振动速度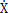 (=rb1sce2θ1
(=rb1sce2θ1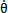 1- rb2sec2θ2
1- rb2sec2θ2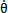 2)有关,文中只列出
2)有关,文中只列出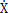 的计算结果,图2-3~图2-13为各种工况的齿轮故障振动分析,其中包括齿轮轮齿相对振动速度时程响应图、齿轮轮齿相对振动速度幅值谱图和相平面图。
的计算结果,图2-3~图2-13为各种工况的齿轮故障振动分析,其中包括齿轮轮齿相对振动速度时程响应图、齿轮轮齿相对振动速度幅值谱图和相平面图。
(l)齿轮工作转速一定时,齿侧间隙的变化对齿轮故障振动频率的影响:
图2-3是工况为:齿轮啮合频率为5888Hz、齿侧间隙b=0齿轮故障振动分析,其中(a)图为齿轮轮齿相对振动速度时程响应图,(b)图为齿轮轮齿相对振动速度幅值谱图。从图上可看出,当齿侧间隙为0时,此时振动故障频率为齿轮啮合频率fmeh。的1、2、3倍。相平面图也稳定于一个椭园极限环(见(c)图)。
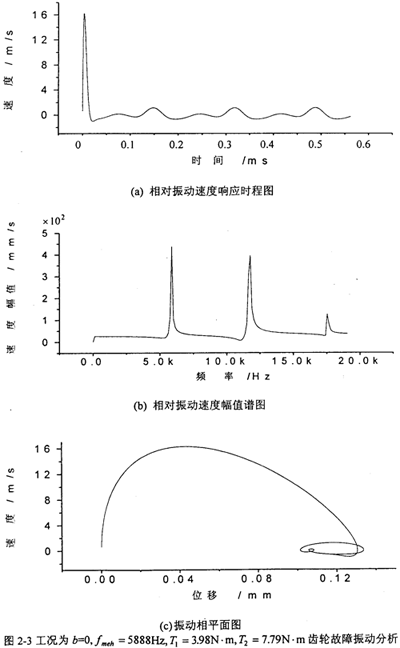
图2-4是工况为:齿轮啮合频率为5888Hz、但齿侧间隙b=0.1mm=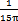 Sn。(齿厚)齿轮故障振动分析,其中(a)图为齿轮轮齿相对振动速度时程响应图,(b)图为齿轮轮齿相对振动速度幅值谱图。从图上可看出,当齿侧间隙增加到O.lmm时,此时振动故障频率仍为齿轮啮合频率fmeh的1、2、3倍。相平面图也稳定于一个封闭曲线(见(c)图)。
Sn。(齿厚)齿轮故障振动分析,其中(a)图为齿轮轮齿相对振动速度时程响应图,(b)图为齿轮轮齿相对振动速度幅值谱图。从图上可看出,当齿侧间隙增加到O.lmm时,此时振动故障频率仍为齿轮啮合频率fmeh的1、2、3倍。相平面图也稳定于一个封闭曲线(见(c)图)。
图2-5是工况为:齿轮啮合频率仍为5888Hz、但齿侧间隙增加到b=0.15mm=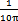 Sn (齿厚)齿轮故障振动分析,其中(a)图为齿轮轮齿相对振动速度时程响应图,(b)图为齿轮轮齿相对振动速度幅值谱图。从图上可看出,当齿侧间隙继续增加到0.15mm时,齿轮轮齿相对振动速度波形有较大的变化,此时振动故障频率成份发生了改变,振动故障频率为齿轮啮合频率fmeh的1/3、2/3、3/3、…倍。极限环经过反复振荡后也稳定于一个封闭曲线(见(c)图)。
Sn (齿厚)齿轮故障振动分析,其中(a)图为齿轮轮齿相对振动速度时程响应图,(b)图为齿轮轮齿相对振动速度幅值谱图。从图上可看出,当齿侧间隙继续增加到0.15mm时,齿轮轮齿相对振动速度波形有较大的变化,此时振动故障频率成份发生了改变,振动故障频率为齿轮啮合频率fmeh的1/3、2/3、3/3、…倍。极限环经过反复振荡后也稳定于一个封闭曲线(见(c)图)。
图2-6对应工况为:齿轮啮合频率仍为5888Hz、但齿侧间隙增加到b=0.20mm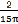 Sn(齿厚)齿轮故障振动分析,其中(a)图为齿轮轮齿相对振动速度时程响应图,(b)图为齿轮轮齿相对振动速度幅值谱图。从图上可看出,当齿侧间隙为0.20mm时,齿轮轮齿相对振动速度波形也有较大的变化,振动速度幅值较前面增加了,此时振动故障频率成份较复杂,振动故障频率为齿轮啮合频率fmeh的1/6、2/6、3/6、…倍。相平面图趋向于一混沌状态边缘(见(c)图)。
Sn(齿厚)齿轮故障振动分析,其中(a)图为齿轮轮齿相对振动速度时程响应图,(b)图为齿轮轮齿相对振动速度幅值谱图。从图上可看出,当齿侧间隙为0.20mm时,齿轮轮齿相对振动速度波形也有较大的变化,振动速度幅值较前面增加了,此时振动故障频率成份较复杂,振动故障频率为齿轮啮合频率fmeh的1/6、2/6、3/6、…倍。相平面图趋向于一混沌状态边缘(见(c)图)。
图2-7是当齿轮啮合频率仍为5888Hz、但齿侧间隙增加到b=0.25mm=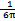 Sn(齿厚)时,齿轮轮齿相对振动速度时程响应图((a)图)和齿轮轮齿相对振动速度幅值谱图((b)图)。从(b)图上可看出,当齿侧间隙增加到0.25mm时,此时振动故障频率成份又发生了改变,振动故障频率为齿轮啮合频率fmeh的l/12、2/12、3/12、…倍。
Sn(齿厚)时,齿轮轮齿相对振动速度时程响应图((a)图)和齿轮轮齿相对振动速度幅值谱图((b)图)。从(b)图上可看出,当齿侧间隙增加到0.25mm时,此时振动故障频率成份又发生了改变,振动故障频率为齿轮啮合频率fmeh的l/12、2/12、3/12、…倍。
图2-8中,(a)图和(b)图分别是当齿轮啮合频率仍为5888Hz、但齿侧间隙增加到b=0.3Omm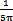 Sn(齿厚)时,齿轮轮齿相对振动速度时程响应图和齿轮轮齿相对振动速度幅值谱图。从(b)图上可看出,当齿侧间隙为0.30mm时,此时振动故障频率成份也发生了改变,振动故障频率为齿轮啮合频率fmeh的1/5、2/5、3/5、…倍。
Sn(齿厚)时,齿轮轮齿相对振动速度时程响应图和齿轮轮齿相对振动速度幅值谱图。从(b)图上可看出,当齿侧间隙为0.30mm时,此时振动故障频率成份也发生了改变,振动故障频率为齿轮啮合频率fmeh的1/5、2/5、3/5、…倍。
总之,齿侧间隙的变化对齿轮故障振动频率有很大的影响。
(2)工作转速对齿轮振动故障频率的影响(此时设齿侧间隙b=0.2mm):
图2-9是当齿轮啮合频率为1300Hz、齿侧间隙b=0.2mm时,齿轮轮齿相对振动速度时程响应图((a)图)和齿轮轮齿相对振动速度幅值谱图((b)图)。从(b)图上可看出,当齿侧间隙为0.2mm时,此时振动故障频率为齿轮啮合频率fmeh的1、2、3倍,分数谐波不明显。
图2-10中,(a)图和(b)图分别是当齿轮啮合频率增加到4000Hz、齿侧间隙增加到b=0.2mm时齿轮轮齿相对振动速度时程响应图和齿轮轮齿相对振动速度幅值谱图。从(b)图上可看出,此时振动故障频率仍为齿轮啮合频率fmeh的1、2、3倍,分数谐波也不明显,但2fmeh的幅值比1fmeh的大。
图2-11中,(a)图和(b)图分别是当齿轮啮合频率为5000Hz、齿侧间隙b=0.2mm时齿轮轮齿相对振动速度时程响应图和齿轮轮齿相对振动速度幅值谱图。从(b)图上可看出,此时振动故障频率发生了改变,振动故障频率为齿轮啮合频率fmeh的1/13、2/13、3/13倍,明显出现分数谐波。
(3)工作载荷幅值的变化对齿轮振动故障频率的影响:
图2-4(b)是轻载时(小的齿侧间隙)齿轮轮齿相对振动速度幅值谱图。从图上可看出,此时振动故障频率为齿轮啮合频率fmeh的1、2、3倍,无分数谐波成份出现。
图2-12是中载、齿侧间隙增大时齿轮轮齿相对振动速度幅值谱图。从图上可看出,此时振动故障频率为齿轮啮合频率fmeh的1/6、2/6、3/6、…倍,分数谐波成份明显。
图2-13是更大的载荷(齿侧间隙保持不变)时齿轮轮齿相对振动速度幅值谱图。从图上可看出,此时振动故障频率为齿轮啮合频率fmeh的l/4、2/4、3/4、…倍,分数谐波成份非常明显。可看出非线性时变系统与线性时变系统和线性系统的齿轮振动故障频率有很大的不同。
2.4 考虑齿轮偏心的振动频谱特征
当只考虑齿轮扭转振动而不考虑齿轮及轴的横向振动时,以往研究都没有考虑到齿轮偏心质量对齿轮扭转振动的影响,实际上这个影响是存在的。不考虑齿侧间隙时,Pn
取(2-2)式,代入式(2-13)可得单级齿轮系统带偏心质量的振动微分方程:
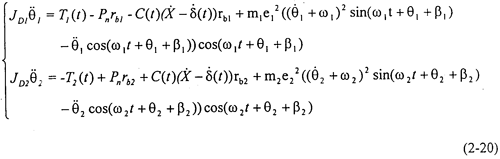
由于θ,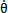 ,
,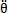 前面的系数和时变刚度K(t)及θ,
前面的系数和时变刚度K(t)及θ,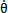 ,有关,不是常数,故方程组(2-14)也是一个非线性时变方程组。
,有关,不是常数,故方程组(2-14)也是一个非线性时变方程组。
采用变步长R-K方法解方程组(2-20),得到齿轮相对振动位移、速度时程响应,如对这时域信号进行FFT变换,就可得到幅值谱。图2-14(a)、2-14(b)分别是考虑齿轮偏心与不考虑齿轮偏心的齿轮振动位移、速度比较图。从图上可看出,考虑齿轮偏心与不考虑齿轮偏心在齿轮振动位移、速度的幅值上是有差别的,前者比后者在最大幅值处大5%左右;两者在振动位移、速度的相位上无差别。图2-15(a)、图2-15(b)是齿轮轮齿相对振动速度时程响应图和齿轮轮齿相对振动速度幅值谱图。从图上可看出,此时振动故障频率发生了改变,振动故障频率除了齿轮啮合频率fmeh的1、2、3倍外,还有齿轮所在轴的轴频。
根据前面的分析结果,我们可认为在分析齿轮的扭转振动故障频率时,由于齿轮轮齿的动力藕合,必须考虑齿轮的偏心质量的影响。
上一页
下一页