(4)振动故障分析
根据第1、2节故障频率计算公式,各轴承的振动故障频率见下表:
表4-l轴承的振动故障频率 (频率单位:Hz)
| 轴承型号 |
故障类型 |
内圈
剥落 |
外圈
剥落 |
钢球
剥落 |
内滚道
不圆 |
保持架不平衡 |
外圈有点蚀 |
内圈有点蚀 |
| 故障频率 |
| f1 |
f0 |
fb |
f,2f,3f,… |
fci |
f0,2 f0,… |
f,2f,… |
23152
(Ⅰ、Ⅳ轴) |
243.3 |
187.9 |
146.5 |
19.2,39.2,58.8,78.4,… |
11.1 |
187.9,375,8,
563.7,… |
243.3,486.6,
729.9,973.2,… |
24148
(Ⅰ、Ⅳ轴) |
231.5 |
180.1 |
153.4 |
19.2,39.2,58.8,78.4,… |
11.0 |
180.1,360.2,
540,3,… |
231.5,463.0,
694.5,926.0,… |
24056
(Ⅱ、Ⅲ轴) |
304.9 |
249.5 |
243.6 |
25.2,50.4,75.6, 100.8,… |
13.9 |
249.5,499,
748.4,… |
304.9,609.8,
914.7,… |
24148
(Ⅱ、Ⅲ轴) |
312.8 |
241.6 |
197.2 |
25.2,50.4,75.6, 100.8,… |
14.2 |
241.6.483.2,
724.8,966,4,… |
312.8,625.6,
938.4,… |
齿轮故障振动频率计算如下:
fz1.2=Z1f=45×19.6=882Hz;fz3.4=Z3f=882 Hz
(5)振动故障分析
在谱图4-3上,五个最大振动速度谱峰所对应的频率分别是:245Hz,97OHz,990Hz,4OHz,485Hz。对照表1,245Hz,485Hz,970Hz分别和I、IV轴上的23152轴承内圈点蚀故障频率243.3Hz,486,6Hz,973.2Hz接近,也和II、III轴上的24148轴承外圈点蚀故障频率241.6Hz,483.2Hz,966.4Hz接近。另外,99OHz是97OHz和I、Ⅳ工V轴轴频19.6Hz的调制。因此可以说明I、IV轴上的23152轴承内圈可能发生了点蚀。谱图4-3上的4OHz对应两倍I、IV轴轴频(=39.2Hz),说明减速机输入轴和电动机转子有些不对中。
在谱图4-4上,五个最大振动速度谱峰所对应的频率分别是:970Hz,240Hz,99OHz,485Hz,95OHz。其中970Hz的振动速度为0.8llmm/s,已超过一级报警值0.65mm/s。对照表4-l,240Hz,485Hz,970Hz分别和I、IV轴上的23152轴承内圈点蚀故障频率243.3Hz,486.6Hz,973.2Hz接近,也和II、III轴上的24148轴承外圈点蚀故障频率241.6Hz,483.2Hz,966.4Hz接近。另外,950Hz和99OHz对应97OHz和I、IV轴一倍轴频19.6Hz的调制。因此可以说明I、IV轴上的23152轴承内圈可能发生了点蚀。
在谱图4-5上,五个最大振动速度谱峰所对应的频率分别是:235Hz, 935Hz,955Hz,117OHz,895Hz。对照表4-1,235Hz,935Hz,1170Hz分别和I、IV轴上的23152轴承内圈点蚀故障频率233.4Hz,933.5Hz,1175Hz接近。另外,955Hz和895Hz分别对应935Hz和I、IV轴一倍轴频19.6Hz和两倍轴频39.2Hz的调制。因此可以说明I、IV轴上的23152轴承内圈发生了点蚀。
在谱图4-6上五个最大振动速度谱峰所对应的频率分别是:235Hz,700Hz,935Hz,117OHz,720Hz。对照表4-l,235Hz,70OHZ,935Hz,117OHz分别对应I、IV轴上的23152轴承内圈点蚀故障频率。另外,72OHz对应700Hz和I、IV轴一倍轴频18.8Hz的调制。因此可以说明I、IV轴上的23152轴承内圈发生了点蚀。
在谱图4-7上,振动速度非常明显的谱峰只有一条,所对应的频率是:235Hz。对照表4-l,它和I、IV轴上的23152轴承内圈点蚀故障频率233.4Hz接近,也和II、III轴上的24148轴承外圈点蚀故障频率231.7Hz非常接近。
在谱图4-8上,振动速度非常明显的谱峰也只有一条,所对应的频率是:235Hz。对照表4-1,它和I、IV轴上的23152轴承内圈点蚀故障频率233.4Hz接近,也和II、III轴上的24148轴承外圈点蚀故障频率231.7Hz非常接近。
(6)结论
综合以上分析,该减速机主要故障发生在I、IV轴上的23152轴承内圈上,也可能发生在Ⅱ、III轴上的24148轴承外圈上,故障类型为点蚀。振动速度虽然超过了一级报警值0.56mm/s,但离二级报警值较远。由于该机组未到大修时间,中间不允许停机检修,故要定期监测该减速机机组,密切注视该减速机机组运行情况。
4.3 基于双时基技术的减速机箱盖振动模态试验
实验模态分析是了解复杂结构动态特性的一个重要工具,为评价设备的动态设计水平并为设备故障诊断排除非故障频率提供了科学的依据。模态试验中,用装有力传感器的手锤进行的冲击激励由于具有设备简单、施力方便、测试速度快等优点,因而在现场模态试验中获得了较广泛的应用。但由于这种方法受冲击产生的脉冲宽度窄以及激励和响应信号采用的等时基采样使得冲击激励的频域细化倍数不能太高,影响了传递函数频率分辨率和导纳精度,因而模态参数的识别精度也就低(对有密集模态的结构尤其严重)。激励和响应如采用两种不同时基采样(即双时基采样)技术即可解决冲击激励法传递函数频率分辨率和精度的矛盾,提高了工程结构的模态分析质量。本文以某减速机箱体上盖的模态分析为例,介绍了变时基技术在冲击激励法模态分析中的应用。
4.3.1 双时基传递函数技术
当用脉冲激励对大型工程结构进行传递函数分析时,一方面,大型工程结构(如汽车、减速机箱体等)固有频率低,需要低频采样(即大的采样时基)才能保证较高的分辨率精度;另一方面,由于脉冲力的作用时间非常短,如要采准信号,采样时间间隔△t必须非常小,即需要很高的采样频率。对于响应和激励采用相同时基、相同窗长的传递函数分析方法是无法克服以上两方面的矛盾。为了解决脉冲力激励系统低频结构传递函数的分辩率和精度的矛盾,本文采用一种不同时基采样为基础的传递函数变窗长细化分析方法,简单介绍如下:
设脉冲激励x(t)和响应信号y(t)分别采用小时基△t1和大时基△t2采样,关系如下:
△t2=m△tl (4-13)
式中m为细化倍数。
通过以上的采样处理,可以得到较多的脉冲信号,从而保证力谱幅值和相位的精度。采样后得到T1、T2两个窗长。
T1=N△t1、T2= N△t2、T2=m*T1 (4-14)
上式中N为采样点数
分析时,可以根据需要的导纳精度和频率分辨率,改变时基和窗长,从而定出细化倍数m,得到一个“双时基、双窗长”的离散时间序列。对这个离散的时间序列进行FFT变换,并采用巧妙的软件技术,可使传递函数H(n △f)的分辨率提高m倍.
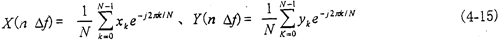
H(n △f)=Y(n △f)/X(n △f) (4-16)
式中△f=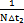 。
。
4.3.2 减速机箱盖模态实验
(l)支撑方案的确定
通常采用橡皮绳将减速机箱盖悬吊起来,虽然可使减速机箱盖获得近似自由支撑状态,但不易得到减速机箱盖全部的模态,另外,试验费用也较高。本实验采用减速机箱体箱盖停放在地面,由木块支撑。
(2)试验频段的选择和采样频率的确定
试验频段的选择应综合考虑减速机箱盖在实际条件下可能的激振频率范围和有限元计算要求。在本实验中,选取0-5OOHz为试验频段。响应采样频率为125OHz。根据经验,力通道采样频率为1OkHz。此时变时基细化倍数为10000/1250=8。传递函数的频率分辨率则为△f=1250/1024=1.22Hz,符合模态分析精度的要求。
(3)激振锤的选择
激振锤的选择包括激振锤大小的选择和激励点数的选择。激振锤的大小选择应充分考虑激励能否提供足够的能量,把所需要频段内的模态全部激发出来。激励点数有单点激励和多点激励两种,它的选择应考虑比较激振锤激振方便和传感器安装方便。由于减速机箱体只有2T重,高度也不大,且我们感兴趣的频段为O-500Hz,故我们用5kg的DFC-2型高性能聚能力锤进行单点激励,传感器采用多点移步拾振。
(4)测点布置的安排
测点布置包括测点位置、测点数量和测量方向的选择。测点的布置既要能够明确反映箱盖所有的模态又要保证我们所关心的结构点(如传感器布置点、外力作用点、重要的响应点、部件或结构的联接点)都在所选的测点之中。
根据以上要求,我们在结构上选取了71个测点,图4-9为测点布置图。
(5)测试系统和模态分析软件
测试系统见图4-10。
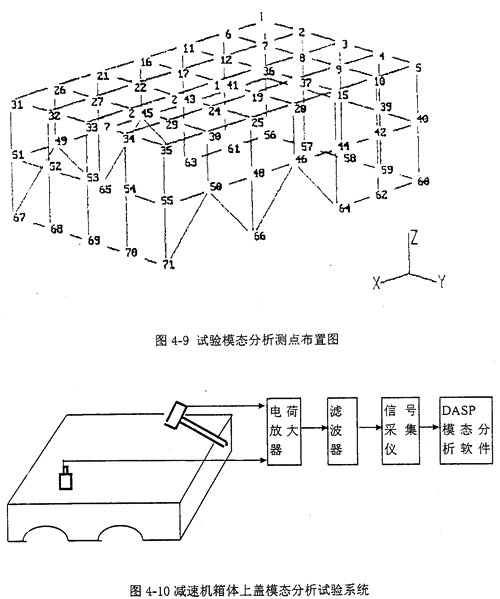
(6)减速机箱体上盖模态试验结果
减速机箱体上盖振动模态可分为减速机箱体上盖侧滚(刚体模态)、减速机箱体上盖整体振动、减速机箱体上盖弯曲和减速机箱体上盖顶盖局部振动。
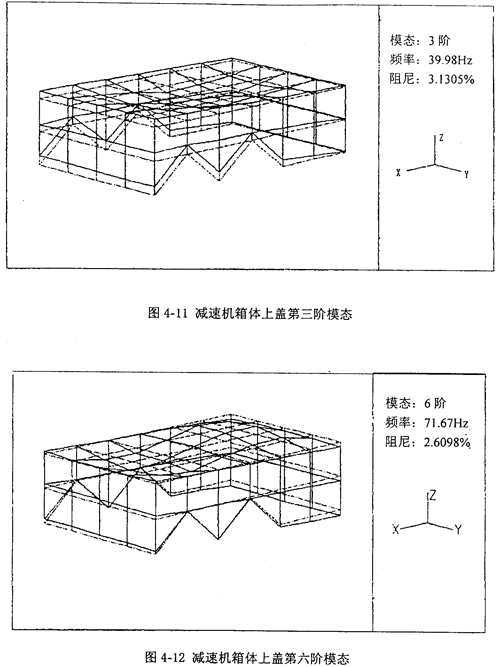
振动模态参数如下表4-2。上盖第三、六弹性模态的对应振型见图4-11和图4-12所示。
表4-2 振动模态参数
| 振型形式 |
模态参数 |
| 频率(Hz) |
阻尼(%) |
| 刚体模态(侧滚) |
21.09 |
3.365 |
| 顶部局部振动 |
26.58,96.07,122.97,319.17 |
1.755,1.529,1.667,0.305 |
| 顶部弯曲振动 |
39.98,50.61,55.49,71.67,
419.87,474.76 |
3.131,1.874,1.928,2.609,0.854,0.372 |
| 整体振动 |
192.62,202.97,223.92,239.42,2
49.48,443.66 |
1.023,2.136,0.622,0.626,0.803,0.603 |
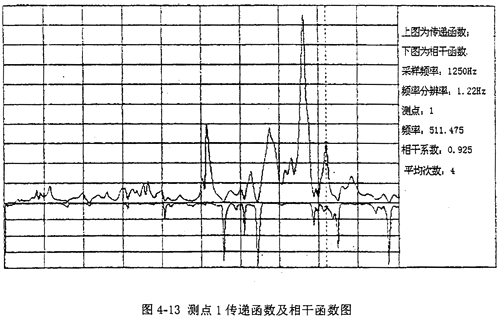
图4-13是测点1垂直方向的传递函数及相干函数图,其它点的传递函数图由于篇幅关系省略。
(6)用模态参数对减速机传动系统的故障诊断提供帮助
这次减速机箱体模态分析试验共做出了17个模态,从振型动画图和振型数据看出,减速机箱体上盖顶部振动稍大一些,因此在布置振动监测传感器时,传感器不能放在减速机箱体上盖顶部。振动模态参数可以帮助从监测信号中区分出那些是传动元件的振动故障频率,哪些是减速机箱体的振动固有频率,从而为减速机传动系统的故障诊断提供帮助。显然,在运行中箱体(包括箱盖)出现的固有频率与由于试验条件情况不同而有差别,这点是要注意的。
4.4 小结
l 分析研究减速机传动元件的故障振动频率,尤其是调心滚子轴承的故障振动频率,对减速机传动系统的故障诊断是至关重要的。
2 基于变时基技术为基础的冲击激励模态分析方法设备简单、频率分辨率高、成本低、测试快是进行减速机箱体动态分析的有效手段,也能对减速机箱体的动态设计水平进行准确的评价。
3 减速机箱体模态分析的结果可为今后故障诊断区别剔除信号中可能出现的减速机箱体固有振动的成分。
上一页
下一页



