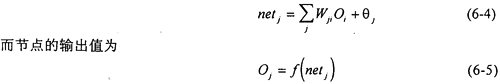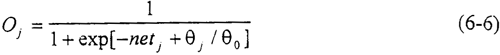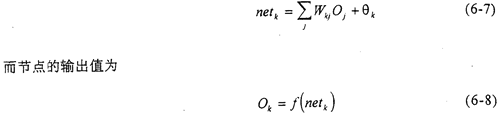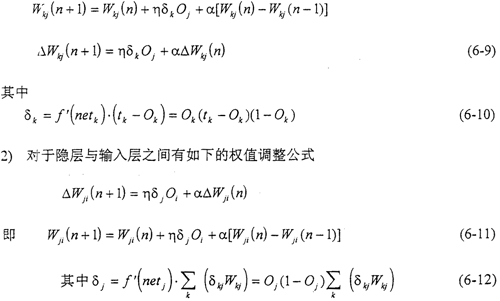第6章 基于神经网络的设备故障智能诊断方法及故障振动趋势分析研究
当前,故障诊断技术发展的一个首要问题就是诊断的智能化。这种智能化主要体现在诊断过程中故障论域专家经验的干预,即在对故障信号进行分析处理及识别的基础上,还需结合故障论域中浅、深知识进行基于知识的诊断推理。这包括两方面的内容:第一,智能型的信号处理技术;第二,智能型的故障识别方法。
故障诊断最终可归结为模式识别这一类问题。从这个基本思想出发,作为诊断分类依据的许多诊断方法被提出,如函数分析法、统计模型分析法、专家系统法、按信息准则的近类分类法、分形几何法和模糊数学综合判别法等等。虽然这些方法已广泛应用于各种故障诊断实例,且取得良好效果,然而一般说来,这些分类方法仅仅是表达了诊断过程某个环节所用的科学理论与工具,并不能反映诊断过程的本质。
复杂机械设备(包括齿轮减速机)的故障与症状之间的关系一般来说是复杂的,难于用一个简单的关系式来表示,有时还具有不确定性,要借助于经验知识和统计来表达。故它的故障诊断用传统的诊断方法是不能取得较好的效果。
人工神经网络(简称神经网络)是近年来掀起热潮的研究领域,它以全新的与传统不同的信息表达和处理方式,对人工智能和故障诊断研究产生了巨大的吸引力。
神经网络是试图模拟人的神经系统而建立起来的自适应非线性动力学系统,网络的拓扑结构和结点的处理功能决定其最大的特点表现为可学习(训练)性和计算巨量并行性及能表达和处理复杂信息关系。神经网络的研究工作可追根溯源四十多年前McCulloch和Pitts及Hebb的工作,其后多种模型和算法已被提出,并得到了广泛深入的研究并应用到设备的故障诊断上。目前在故障诊断中应用最广泛的算法是BP算法。
本章研究了常用的基于BP算法的神经网络对机械设备的诊断。本章根据故障诊断经验知识和现场故障排除统计及齿轮减速机故障振动机理的研究对已有的齿轮减速机故障训练样本进行了完善,并用基于改进的MBP算法的神经网络对实际的齿轮减速机故障进行了诊断研究。
故障振动趋势分析研究是本章要研究的另一个问题。趋势分析是故障诊断中的一个重要环节,其主要任务是对设备的故障发展趋势或劣化趋势作出估计和预测。通过趋势分析,可对设备进行事故预防和无破坏性监测,充分发挥设备的工作潜力,合理安排生产。
根据采集的故障振动数据序列是平稳时间序列还是非平稳时间序列,振动故障趋势分析可分别采用AR(M)模型和GM(1,1)及AR(M)组合模型,也可采用预报精度较高的神经网络组合预报模型。
6.1 基干BP算法的设备故障智能诊断方法
BP算法即是误差反传训练算法,它是一种有导师的训练算法,它在给定输出目标的情况下,按其实际输出与目标值之差的平方和为目标函数,通过调节权值使目标函数达到最小值。多层感知器前馈BP网络模型如图6-1所示。
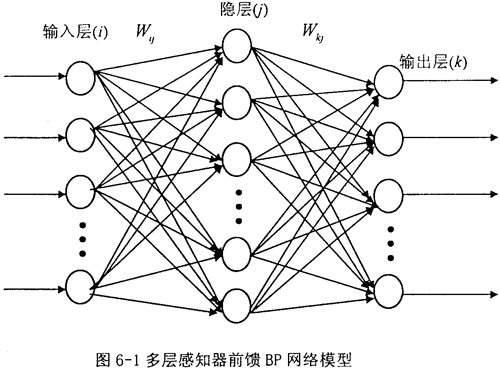
前馈网络的训练学习是一种监督学习,而监督学习的范例要求每一个输入模式矢量与表示所期望的输出模式矢量必须配对。一般说来,网络输出值{OPK}与期望的输出值{tPK}是不相等的。对每一个输入模式的模式样本,其平方误差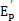 为:
为:

式中,p=1~N,N为输入模式模式样本总数。而对于所有的学习样本,网络均方程差:

对于图6-1所示的网络,其训练学习的过程包括:1)网络内部的前向计算;2)误差的反向传播。其主要目的就是通过逐步调整网络的内部连接权值,使网络的均方误差达到我们的要求。网络内部的连接权值的调整,都是采用推广的δ规则来完成的。
6.1.1 网络内部的前向计算过程:
1)网络输入模式的各分量作为第i层(输入层)节点的输入。这一层节点的输出完全等于它的输入值。即:
Oi=Ii (6-3)
2)网络第j层(即隐层)节点的输入值为
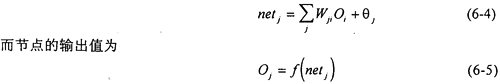
其中Wji为隐层的节点j与输入层的节点i之间的连接权值,θj为隐层节点j的阀值,而f为节点的激励函数,可采取如下单调递增的激励函数:
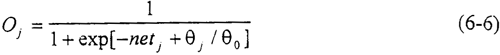
其中θ0的作用是改变激励函数的形状。
3)网络第k层(即输出层)节点的输入值为
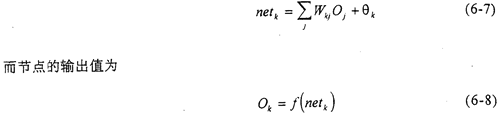
其中Wkj输出层节点k与隐层的节点j之间的连接权值,θk为隐层节点k的阈值。
6.1.2 误差的反向传播过程
1)设n为迭代次数,对于输出层与隐层之间有如下的权值调整公式
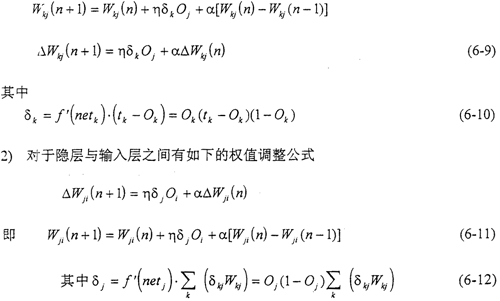
α为惯性因子,用于调整网络学习的收敛速度,适当的α值会有利于抑制振荡,α为惯性因子,用于调整网络学习的收敛速度,适当的α值会有利于抑制振荡,η为学习步长,即权值增益因子。一般它们的取值范围为:0<α<1,0<η<1。
6.1.3 算例1
在大型旋转机械中,转子不平衡、转子不对中、油膜涡动、油膜振荡、喘振、旋转失速等是比较常见的几种故障。这里采用了幅值谱中七个频段上的幅值作为网络的输入样本模式对这几种常见故障进行分类。
在诊断之前,先建立故障的标准归一化模式样本,见表6-1(表中f为轴的转动频率)。将这些样本用于网络训练,然后,将这些训练好的样本应用于某大型机组中,不断地积累该机组的各种故障模式样本,再加到训练样本中,通过训练学习可以得到该机组的故障识别神经网络,从而在该机组的实际故障诊断中获得较高的识别精度。表6-2为标准训练样本的训练结果,表6-3为待识别的故障样本,表6-4为待识别的故障样本的识别结果。本算例网络规模为:输入层节点数为:7个;一个隐层节点数为:10个;输出层节点数为6个;误差精度为10-5;网络迭代次数为12000次。
表6-l 标准训练样本
故障
样本 |
0.01~0.40f |
0.41~0.50f |
0.51~0.99f |
lf |
2f |
3f~sf |
5f |
理想
输出 |
| 不平衡 |
0.0000 |
0.0000 |
0.0000 |
1.0000 |
0.0056 |
0.0055 |
0.0000 |
100000 |
| 不对中 |
0.0000 |
0.0000 |
0.0000 |
0.8000 |
1.0000 |
0.0200 |
0.0000 |
010000 |
油膜
涡动 |
0.0000 |
0.6534 |
0.0000 |
1.0000 |
0.0100 |
0.0084 |
0.0000 |
001000 |
油膜
振荡 |
0.0000 |
0.9543 |
0.0000 |
1.0000 |
0.0100 |
0.0081 |
0.0000 |
000100 |
| 喘振 |
0.8546 |
0.0000 |
0.0000 |
1.0000 |
0.1262 |
0.1045 |
0.1105 |
000010 |
旋转
失速 |
0.9032 |
0.0000 |
0.7056 |
1.0000 |
0.2854 |
0.1539 |
0.1135 |
000001 |
表6-2 标准训练样本的训练结果
| 故障样本 |
不平衡 |
不对中 |
油膜涡动 |
油膜振荡 |
喘振 |
旋转失速 |
| 不平衡 |
0.9487 |
0.0058 |
0.0123 |
0.0000 |
0.0065 |
0.0006 |
| 不对中 |
0.0054 |
O.9489 |
0.0000 |
0.0000 |
0.0015 |
0.0036 |
| 油膜涡动 |
0.0006 |
0.0007 |
0.9399 |
0.0131 |
O.0031 |
0.0005 |
| 油膜振荡 |
0.0000 |
0.0012 |
0.0209 |
0.9468 |
0.0014 |
0.0012 |
| 喘 振 |
0.0067 |
0.0036 |
0.0019 |
0.0000 |
0.9480 |
0.0068 |
| 旋转失速 |
0.0009 |
0.0031 |
0.0002 |
0.0000 |
0.0073 |
0.9489 |
表6-3 待识别的故障样本
| 故障样本 |
0.01~0.4Of |
0.41~O.50f |
0.51~0.99f |
1f |
2f |
3f~5f |
5f |
实际输出 |
| 待识别 |
0.0000 |
0.0000 |
0.0000 |
0.8510 |
1.0000 |
0.0250 |
0.0000 |
未知 |
| 待识别 |
0.6501 |
0.0000 |
0.0000 |
1.0000 |
O.0000 |
0.1254 |
0.1159 |
未知 |
| 待识别 |
0.0000 |
0.6820 |
0.0000 |
1.0000 |
0.0120 |
O.0086 |
0.0000 |
未知 |
表6-4 待识别的故障样本的识别结果
| |
不平衡 |
不对中 |
油膜涡动 |
油膜振荡 |
喘振 |
旋转失速 |
| 故障1 |
0.0083 |
0.9413 |
0.0000 |
0.0000 |
0.0015 |
0.0033 |
| 故障2 |
0.0716 |
0.0020 |
0.0046 |
0.0000 |
0.7752 |
0.0035 |
| 故障3 |
0.0003 |
0.0007 |
O.9049 |
0.0266 |
0.0029 |
0.0005 |
BP训练算法已成功地应用于广泛的问题,但是它训练过程存在着不确定性。比如,对于一些复杂的问题,它可能要训练几天以至几周的时间,甚至根本不能训练。冗长的训练时间,可能是由不适当的调节阶距引起的,也就是与选取的训练步长太小有关。完全不能训练,则一般由两种原因引起的:一是网络的麻痹现象,另一是局部最小。
针对BP训练算法存在的问题,人们提出了许多改进算法,针对训练速度问题,人们提出了回归算法、样本添加法、双BP算法等改进算法;针对网络完全不能训练问题,人们提出了改进误差函数和统计训练算法等改进算法。
上一页
下一页