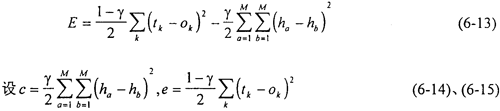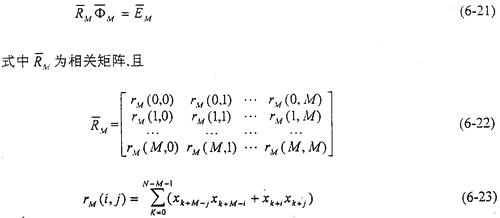6.2 基于MBP算法的设备故障智能诊断方法
普通BP训练算法在它的训练过程存在着不确定性除了上节提出的一些因素外,还有一个重要的原因,就是它的误差函数不尽合理。它的误差函数决定了靠近网络输出端的权在训练一开始调整较大,而远离输出端的权在训练过程中调整始终较小,从而把网络训练速度降低,甚至把网络引入训练不收敛的地步。本节针对这种情况,采用一种新误差函数,保证不管远离还是靠近网络输出端的权在训练时同步调整,提高了网络训练速度和网络收敛性,基于新的误差函数的算法称为MBP算法。算法如下:
误差函数:
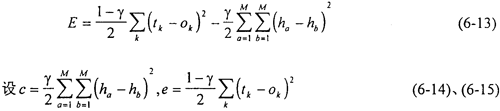
式中γ为隐层与输入层权值参与因子,ha和hb分别为隐层的输出。
6.2.1 误差的反向传播过程
1)对于输出层与隐层之间有如下的权值调整公式

式中α和η的解释同上节。对于小型网络,γ可取较大的值,一般为0.004~0.016,对于大的网格,γ应取较小的值,一般为0.00001~0.00022。
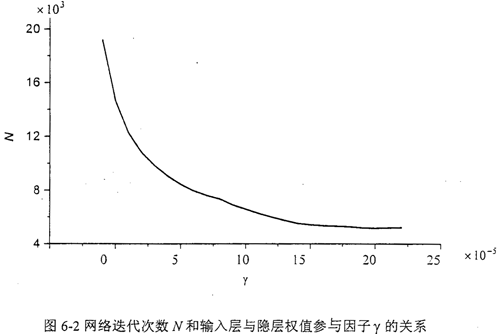
以表6-1标准训练样本为例,采用MBP法,网络有较好的收敛性,训练速度有较大的提高,见图6-2。图中,当γ=0时,MBP法即为普通的BP算法。
6.2.2 算例
由于减速机故障样式的多样性,故它的故障标准模式样本的建立是比较困难的,需进行大量的试验研究和实际设备故障诊断的总结和归纳。表6-5是在参考其它学者研究成果的基础上,总结设备具体工作情况得出的减速机的故障标准模式样本,表6-6为减速机标准训练样本的训练结果(网络规模为:输入层节点数为:9个;一个隐层节点数为:40个;输出层节点数为9个;误差精度为10-5,网络迭代次数为5217次)。图6-3为某一有故障的轧钢减速机的时域信号,图6-4为频域信号。对图6-4的频域信号进行归一化处理,可得待识别的故障样本,用训练好的网络对该样本进行识别。表6-7为该减速机故障样本的识别结果。fa一轴频,f0一轴承外圈故障特征频率,fi一轴承内圈故障特征频率,fb一轴承滚动体故障特征频率,fmeh一齿轮啮合频率。
表6-5 减速机的故障标准模式样本
| 故障类型 |
故障特征频率及重要度 |
理想
输出 |
| fa |
2fa |
3~4fa |
f0
2f0 |
f1
2f1 |
fb
2fb |
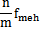 |
fmeh |
2.3
fmeh |
| 轴 |
轴不平衡或弯曲 |
1.000 |
0.50 |
0.050 |
0.000 |
0.000 |
0.000 |
0.000 |
0.050 |
0.050 |
10000000
0 |
| 轴线不对中 |
0.800 |
1.000 |
0.080 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
01000000
0 |
| 轴生裂纹 |
1.000 |
0.800 |
0.600 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
00100000
0 |
轴
承 |
外滚道损伤类 |
0.000 |
0.000 |
0.000 |
1.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
00010000
0 |
| 内滚道损伤类 |
0.000 |
0.000 |
0.000 |
0.000 |
1.000 |
0.000 |
0.000 |
0.000 |
0.000 |
00001000
0 |
| 滚动体损伤类 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
1.000 |
0.000 |
0.000 |
0.000 |
00000100
0 |
齿
轮 |
全面点蚀或完全磨损 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
1.000 |
0.400 |
0.400 |
00000010
0 |
| 局部齿面损伤 |
0.400 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.600 |
0.600 |
00000001
0 |
| 两齿轮轴不平行 |
0.700 |
0.400 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.600 |
0.600 |
00000000
1 |
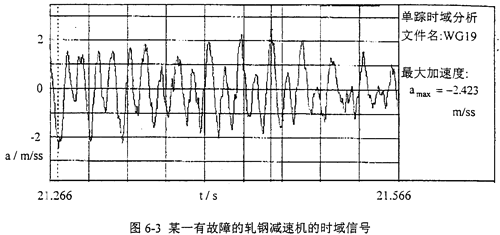
表6-6 标准训练样本的训练结果
故障
样本 |
轴不平衡或弯曲 |
轴线不对中 |
轴生
裂纹 |
外滚道损伤类 |
外滚道损伤类 |
滚动体损伤类 |
全面点蚀或完全磨损 |
局部齿面损伤 |
两齿轮轴不平行 |
轴不平衡
或弯曲 |
0.9906 |
0.0000 |
0.0070 |
0.0024 |
0.0028 |
0.0031 |
0.0012 |
0.0026 |
0.0000 |
轴线
不对中 |
0.0003 |
0.9904 |
0.0085 |
0.0004 |
0.0031 |
0.0010 |
0.0013 |
0.0005 |
0.0008 |
| 轴生裂纹 |
0.0071 |
0.0081 |
0.9894 |
0.0042 |
0.0004 |
0.0014 |
0.0006 |
0.0000 |
0.0000 |
外滚道
损伤类 |
0.0015 |
0.0002 |
0.0008 |
0.9926 |
0.0034 |
0.0036 |
0.0028 |
0.0025 |
0.0000 |
外滚道
损伤类 |
0.0029 |
0.0035 |
0.0000 |
0.0031 |
0.9930 |
0.0036 |
0.0030 |
0.0018 |
0.0000 |
滚动体
损伤类 |
0.0022 |
0.0006 |
0.0000 |
0.0026 |
0.0030 |
0.9933 |
0.0027 |
0.0022 |
0.0000 |
| 全面点蚀或完全磨损 |
0.0007 |
0.0008 |
0.0000 |
0.0026 |
0.0032 |
0.0026 |
0.9929 |
0.0033 |
0.0000 |
局部齿
面损伤 |
0.0056 |
0.0000 |
0.0000 |
0.0039 |
0.0025 |
0.0023 |
0.0042> |
0.9886 |
0.0133 |
两齿轮轴
不平行 |
0.0002 |
0.0048 |
0.0001 |
0.0007 |
0.0004 |
0.0007 |
0.0034 |
0.0105 |
0.9845 |
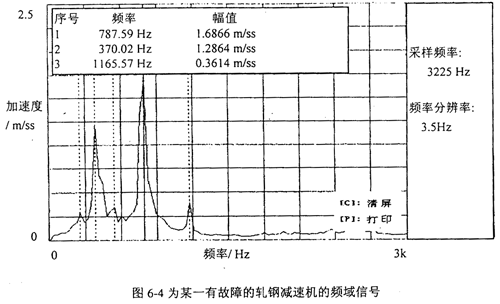
表6-7 该减速机故障样本的识别结果
故障
类型 |
轴不平衡
或弯曲 |
轴线不
对中 |
轴生
裂纹 |
外滚道
损伤 |
内滚道
损伤 |
滚动体
损伤 |
齿面点蚀或
完全磨损 |
局部齿
面损伤 |
齿轮轴
不平行 |
故障
程度 |
0.017 |
0.002 |
0.000 |
0.002 |
0.017 |
0.003 |
0.987 |
0.000 |
0.000 |
表6-7 识别结果与实际诊断结果一致
6.3 基于AR(M)模型的平稳时序故障振动趋势分析
通过对所记录的故障振动数据序列的均值μx和方差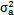 的检验,可判别出该振动数据序列是平稳时间序列还是非平稳时间序列,从而为故障振动趋势分析研究的建模提供了准备。对平稳时间充列可采用较简单的AR(M)模型建模和振动故障趋势分析;对非平稳时间序列可采用较实用的GM(1,1)模型及AR(M)组合模型建模和振动故障趋势分析,也可采用预报精度较高的神经网络组合预报模型,此内容见6.5节和6.6节。
的检验,可判别出该振动数据序列是平稳时间序列还是非平稳时间序列,从而为故障振动趋势分析研究的建模提供了准备。对平稳时间充列可采用较简单的AR(M)模型建模和振动故障趋势分析;对非平稳时间序列可采用较实用的GM(1,1)模型及AR(M)组合模型建模和振动故障趋势分析,也可采用预报精度较高的神经网络组合预报模型,此内容见6.5节和6.6节。
6.3.1 AR(M)模型的建模
模型的建模包括以下过程:
1)数据的采集;
2)数据的预处理:包括提取趋势项、零化处理及标准化处理;
3)AR(M)模型的参数估计
对于AR(M)模型,时间序列xt可表示为:
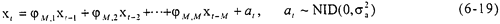
所谓参数估计,是指根据经检验和预处理后的时序按某一方法估计出式(6-19)中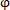 M,1,
M,1,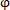 M,2,
M,2,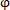 M,3,…,
M,3,…,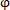 M,M和
M,M和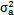 这M+1个参数。AR(M)模型的参数估计方法有许多种,较易用计算机编程实现的方法是Marple参数递推估计法。
这M+1个参数。AR(M)模型的参数估计方法有许多种,较易用计算机编程实现的方法是Marple参数递推估计法。
正推、反推预报误差的平方和总能量εM:

Marple方法是利用最小二乘法使正推、反推预报误差的平方和总能量εM最小来估计AR(M)模型的参数的。使εM对所有的自回归参数的导数等于零,可得到下列方程:
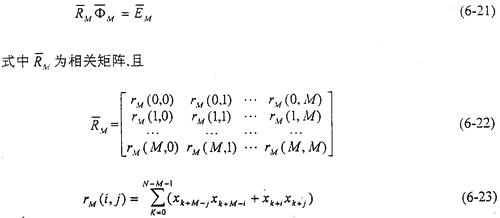
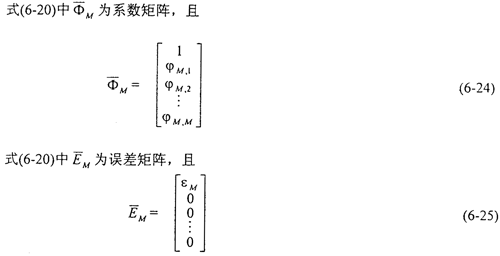
根据自相关矩阵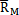 的特点,可将
的特点,可将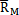 相关矩阵(6-22)式表示为Toeplity矩阵和Hankel矩阵相乘,使求解AR(M)模型参数
相关矩阵(6-22)式表示为Toeplity矩阵和Hankel矩阵相乘,使求解AR(M)模型参数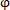 M,j(j=1,2,…,M)的计算工作量为NM+O(M2)次运算。其中N为输入数据长度,M为AR模型的阶数,O(M2)为最高次数为2的代数式。
M,j(j=1,2,…,M)的计算工作量为NM+O(M2)次运算。其中N为输入数据长度,M为AR模型的阶数,O(M2)为最高次数为2的代数式。
上一页
下一页