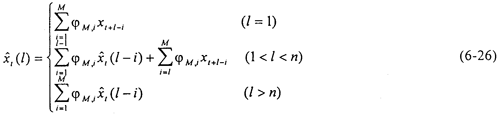6.3.2  平稳时序故障振动趋势分析

根据最佳预测原理，可推出AR（M）模型的最佳趋势分析算式为：

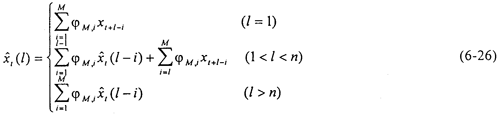
AR（M）模型的最佳趋势分析模型的递推计算不涉及{a_t}，从而就不必使用时序的全部数据，而只用到x_t，x_t-1，…，x_t+1-n这n个数据，计算量少。

6.3.3  算例

本节对在某车床上采集的振动信号用AR（M）模型进行预测，表6-8为测试数据值，预测结果见图6-5（图中，a-振动加速度，t-时间），与实测结果相比，AR（M）模型预测误差最大点为6.22%，最小点为0.34%，基本符合预测要求。

表6-8  某车床振动信号测试数据（时间单位：min；振动值单位：mv）

时间	振动	时间	振动	时间	振动	时间	振动	时间	振动	时间	振动	时间	振动	时间	振动	时间	振动
1	122	14	143	27	124	40	126	53	129	66	125	79	126	92	111	105	138
2	135	15	123	28	122	41	118	54	125	67	119	80	139	93	131	106	131
3	122	16	112	29	127	42	154	55	121	68	121	81	129	94	129	107	121
4	116	17	125	30	127	43	109	56	126	69	117	82	121	95	117	108	128
5	134	18	135	31	113	44	138	57	129	70	127	83	134	96	133	109	122
6	127	19	127	32	133	45	120	58	132	71	135	84	115	97	121	110	127

7	114	20	131	33	118	46	124	59	129	72	111	85	125	98	131	111	131
8	127	21	120	34	134	47	120	60	121	73	124	86	127	99	127	112	123
9	119	22	127	35	130	48	131	61	123	74	140	87	125	100	113	113	119
10	120	23	131	36	127	49	113	62	131	75	122	88	125	101	126	114	134
11	136	24	114	37	117	50	139	63	131	76	113	89	129	102	136
12	122	25	123	38	138	51	120	64	123	77	142	90	124	103	124
13	121	26	130	39	123	52	115	65	131	78	118	91	122	104	147

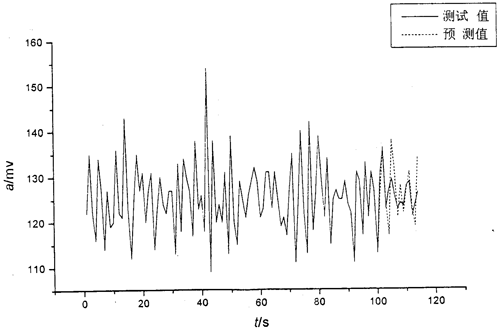
图6-5AR（M）模型振动预测

6.4  基于GM（1，1）模型的非平稳时序故障振动趋势分析

6.4.1  GM（1，1）模型

GM（1，1）模型是最简单的灰色模型，称为一阶灰色模型。根据灰色系统理论，对时间序{x_t}（t=1，2，…，N）进行一次累积生成处理，

可得到一个生成序列{x_t⁽¹⁾}（t=1，2，…，N），对此生成序列建立如下的一阶微分方程：

上式成为GM（1，1），其中a,u为模型参数，根据微分方程理论，GM（1，1）的解为：

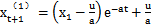                          （6-29）

6.4.2  GM（1，1）建模

（1）对监测时序{x_t}（t=1，2，…，N），按式（6-27）进行一次预处理，得到一个生成序列{x_t⁽¹⁾}（t=1，2，…，N）。

（2）构造数据矩阵，

6.4.3  建模特点

通过对时间序列的预处理，可使{x_t}中所包含的确定性信息因相互叠加而得到加强，同时随机性成分在预处理时相互抵消一部分而不为减弱，从而便于从{x_t}序列中提取指数趋势项，为故障趋势分析打下基础。

6.4.4  非平稳时序故障振动趋势分析

对（6-30）式求导或做累减还原处理，可得原始时间序列{x_t}的预测公式：

x_t+1=（-ax₁+u）e^-at                          （6-33）

因此非平稳时序中指数趋势项的预测公式（l步）为：

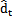（l）=（-ax₁+u）exp[-a（t+l-1）]                  （6-34）

对{x_t}中乘下的残差序列{ε_t}（是一个稳态序列）建立AR（M）模型，并按（6-26）式进行l步预测。故非平稳时序振动故障趋势分析公式为：

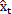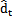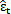（l）=（l）+（l）                      （6-35）

6.4.5  算例

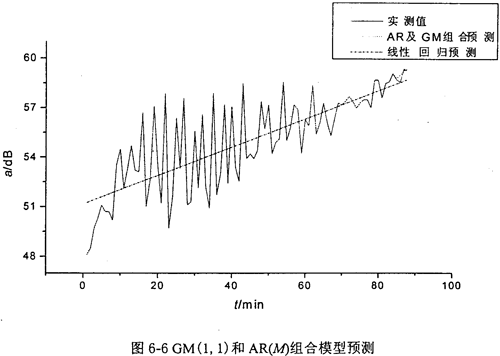
表6-9是在某轴承座上测得的振动加速度信号，经检验该时间序列为一个非平稳序列，现用GM（1，1）和AR（M）组合模型预测第85至第88个数据点，预测结果见图6-6。预测误差最大点为1.7%，最小点为0.33%。图6-6中还画出了有线性回归模型预报的结果，预报误差最大达2.23%。

表6-9  某轴承座振动加速度信号（时间单位：min，振动值单位dB）

时间	振动值	时间	振动值	时间	振动值	时间	振动值	时间	振动值	时间	振动值	时间	振动值	时间	振动值
1	48.2	12	53.3	23	49.7	34	50.9	45	54.2	56	55.8	67	55.3	78	57.0
2	48.5	13	54.7	24	51.6	35	57.9	46	53.9	57	57.2	68	56.3	79	58.7
3	49.7	14	53.2	25	56.4	36	51.7	47	54.4	58	56.9	69	57.3	80	58.7
4	50.3	15	53.1	26	53.3	37	53.0	48	57.4	59	54.2	70	57.2	81	57.6
5	51.1	16	56.7	27	57.6	38	57.2	49	55.7	60	56.3	71	57.4	82	58.5
6	50.7	17	51.0	28	51.1	39	52.4	50	57.2	61	55.9	72	57.7	83	58.6
7	50.7	18	52.6	29	51.3	40	57.1	51	54.2	62	58.4	73	57.4	84	59.1
8	50.2	19	57.1	30	55.6	41	53.4	52	54.9	63	55.4	74	57.0	85	58.7
9	53.5	20	53.5	31	52.1	42	52.5	53	55.1	64	56.1	75	57.3	86	58.6
10	54.5	21	51.2	32	56.6	43	58.5	54	58.7	65	57.3	76	57.5	87	59.4
11	52.1	22	57.9	33	52.2	44	53.9	55	55.0	66	56.1	77	57.5	88	59.2

 

 

 

 

 

 

 

6.5  基于神经网络的故障振动组合预报模型

传统的组合预报模型由于存在一是对模型结构作了限定，二是受参数优化准则形式制约等缺点，使得其适用性受到限制，而神经网络模型由于不需要建立反映系统物理规律的数学模型和其极强的非线性映射能力，使得它能更好地解决实际复杂问题，如振动预报问题。图6-7是神经网络和其它模型组合起来的预报模型。

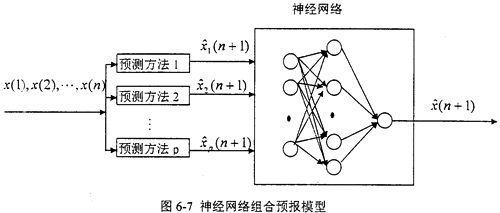
图6-7中，神经网络的输入为p种预测方法（包括AR、ARMA、回归、灰色和直接神经预测等模型）的输出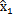(n+1)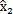，(n+l),…，(n+1)，输出为最终预报值（n+1）。

6.5.1  模型特点

神经网络组合预报模型可提高参与组合的传统时间序列预报方法的预报精度。同传统的非线性组合预报模型相比，神经网络组合预报模型在提高预报精度的同时不需对模型结构作限制。把这种技术应用于振动故障诊断和趋势预报，对提高系统的故障早期发现能力，避免关键设备发生突发事故有着极其重要的意义。

6.5.2  算例

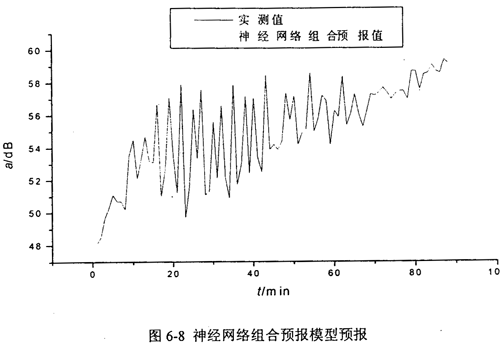
对表6-9提供的数据采用神经网络组合预报模型预报预测第81至第88个数据点。先对表6-9提供的第1至第80个数据点采用AR-GM(1,l）模型和线性回归模型建模，然后用这两个模型对未来8个数据点预测。网络的输入采用AR-GM(1,1）模型和线性回归预报结果，网络经过训练后，网络的预报值见图6-8（网络规模为：输入层节点数为：2个；一个隐层节点数为：10个；输出层节点数为1个；误差精度为10-5；网络迭代次数为1256次）。与AR-GM(1,1）模型和传统的线性回归预报结果相比较，神经网络组合预报模型预报值与实测值之间的误差仅为0.16%，预报精度最高。

6.6  小结

本章以神经网络技术为工具，从模式识别的角度较为详细地讨论了该技术在大型旋转机械故障诊断中的应用。本章还研究了改进的BP算法对网络训练速度的影响，结果表明该方法可提高网络训练速度70%。此外，利用改进的MBP算法训练的网络对实际的大型减速机故障进行诊断，可得到与实际情况诊断较为一致的结论。

本章通过用自回归AR（M）模型对所采集的设备振动平稳信号进行振动故障趋势分析，或用灰色GM(l,l）及自回归AR（M）组合模型对所采集的设备振动非平稳信号进行振动故障趋势分析，并把趋势预测结果与实测值相比，发现趋势预测误差较小。研究结果也标明，当采用神经网络组合预报模型作为预测模型时，预报精度还可提高。

上一页

下一页