第2章 等角速万向联轴器理论
2.1 引言
等角速万向联轴器机构的发明及应用开辟了万向联轴器的开发和应用的崭新时代,它也是万向联轴器等角速运动的基础和灵魂。对它的创新意味着有可能发明出新型的等角速万向联轴器,研究意义重大,万向联轴器机构等角速传动的理论研究因此也成为该领域一个重要的研究课题。
实现等角速传动,可以有多种形式。可以用高副机构也可以用低副机构,可以在两轴间用多个构件也可以用单一构件,可以用连杆也可以用滚子或其它形状的构件。正是由于这些不同的型式,通过型演化就会产生更多的、千变万化的等角速机构。这也是等角速理论复杂的原因所在。
本章从等角速回转连杆机构入手,以实际的几种典型等角速产品为例,对不同的等角速理论进行理论推导,分析和综合,给出了它们不同的适用范围,为新型等角速联轴器机构的发现提供必要的理论基础。
2.2 等角速回转连杆机构探讨
在等角速万向联轴器中,大部分都属于连杆机构.最古老的双联十字轴万向联轴器机构就是球面四连杆机构。从大量的不同的机构综合中,有可能得出多种实用的等角速连杆机构,所以研究等角速理论,以连杆机构的型式和尺度关系为对象,进行新的等角速理论的探索,在一定的意义上是可行的。在机构学上,构件同构件间的连接称为副,其不同的形式和代号如图2-1所示:
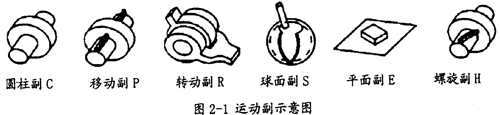
2.2.1 等角速回转连杆机构
等角速回转连杆机构可用于任意位置轴间的等角速传动,如相交轴、交错轴(interlaced shaft)、平行轴。与齿轮机构相比,它一般具有构件简单、容易制造、传动精度高、耐磨损等优点。现已被广泛应用于汽车、轧钢机等设备的双联十字轴万向联轴器、十字滑块联轴器等机构就是其代表。
等角速回转连杆机构大多为空间机构,解析较繁难,其尺度约束关系式较复杂。对它的研究,只能从某些方向着手,目前我国有的学者利用基本的回转机构等角速理论为出发点,利用机构学中型演化和运动链叠加等方法得出了多种具有等角速特性的机构。其理论和方法如下:
基础理论:
若一个机构在运转时其位形始终具有以轴交角(输人轴和输出轴之间的夹角)的角平分面为镜面的对称性,则该机构将具有等角速性。显然,运动副与构件均对称于上述镜面且含有中间副的单自由度镜面机构是这类机构的基本型式,其运动特征是,中间运动副始终在镜面内作平面运动。这一理论直观地阐明了一般相交轴、交错轴等角速连杆机构的基本型式。
镜面机构的中间运动副应始终作镜面内的平面运动,可假想构成中间运动副的两构件分别与镜面构成假想平面副而形成了两个对称于镜面的假想机构。称此假想机构为“假想半联轴器机构”。
采用的方法:
对于上述的单自由度镜面机构,引人“假想半联轴器机构”的概念来阐明一般相交轴、交错轴等角速传动连杆机构的构成型式,从而将通常十分繁难的等角速多杆空间机构尺度关系的研究,简化为“假想半联轴器”联轴器机构曲柄条件的研究。应用静力平衡法进行求解,即得出它们的曲柄存在的条件,也就得到了此机构等角速回转的尺度约束关系式。
通过上述的方法,可以得到相交轴、交错轴形式的多种等角速连杆机构。在图2-2中列出了其中的一部分,它们都是相交轴传动的形式,当然全都是镜面机构。在这些机构中有的已被应用在等角速联轴器上,如球铰柱塞式万向联轴器就是以RPSPR机构为基础。在图2-3中列出了其中的一种较重要的交错轴形式的等角速连杆机构。
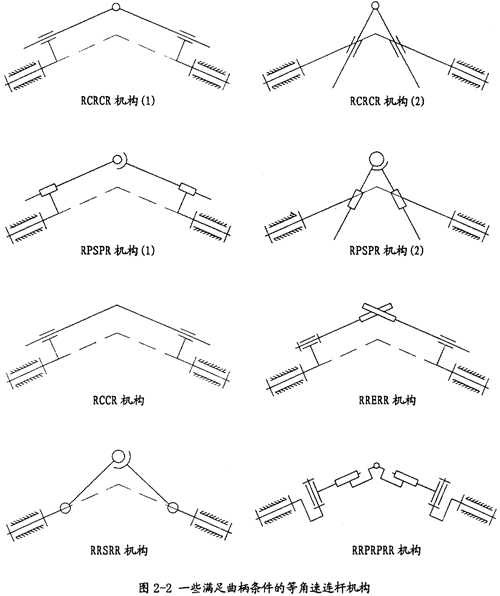
在图2-3所示的RCRCR镜面交错轴等角速连杆机构中,要保证这种机构存在双曲柄,必须满足许多条件,图中所示的红色尺寸值d相等只是其中的一个,从这一约束关系,就可以看出,在等角速机构中要实现机构的等角速性能,不但需要满足机械中各构件自身的形状尺寸,而且也要满足构件间的相互空间位置关系。鉴于图2-3中所示的空间位置表达不清晰,特绘制了它的装配模型图和机构的各零件模型图,分别如图2-4、图2-5所示。
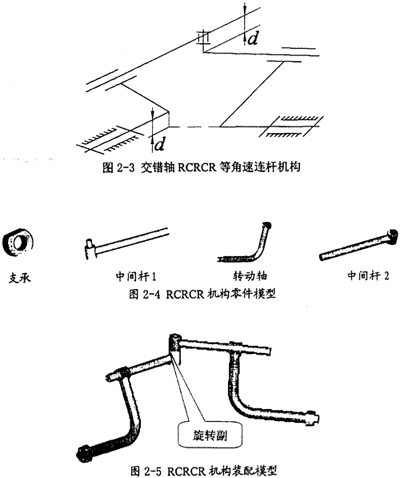
利用图2-5中的机构形式,将其在空间中进行扩展,即可得到一种非常有价值的等角速万向联轴器——RCRCR交错轴等角速万向联轴器。在图2-6示意了此种联轴器的组成零件模型,在图2-7中示意了此种联轴器的装配模型,其中左右两图分别是从不同的视角得到的视图。这种联轴器在功能上能实现空间交错轴传动,它的主要特点是:低副结构,耐磨损性好;构件形状简单,便于制造;允许被联接的两交错轴的偏移角变动范围大,甚至可作直角交错传动(不考虑构件间干涉时)。

2.2.2 等角速连杆机构的验证
上述的理论是在镜面机构(据现有的理论是等角速度机构)的基础上,解出曲柄条件,得到机构等角速运动的尺宽约束关系式。为了验证这一方法的可行性,特制作了如正气RPSPR平面相交轴模型(如图2-8所示),这个模型的结构左右未完全对称(两个移动副到球面副的距离不同)。
2.2.2.1 仿真模型的建立
在图2-8所示模型的基础上,通过在各构件间加上运动副,在运动副上施加运动驱动,即可得到此机构的运动仿真模型(如图2-9所示)。在此模型的建立过程中严格保证各构件的共面,其运动副的形式同图2-2中的RPSPR机构均相同。这样在此模型中有4个构件(不含机架)、有2个旋转副、有2个移动副、有l个球面副、模型有l个自由度,再加上l个运动驱动即可得到完整的仿真模型。不过此模型并不满足镜面机构的条件。
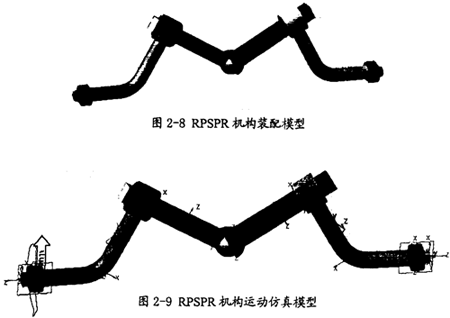
2.2.2.2 仿真结果分析
对模型进行运动仿真分析,并输出此模型的输入和输出角速度的测量曲线(如图2-10所示)。
在此仿真中共输出了此模型运动两周的曲线,这证明此模型中双曲柄肯定存在,按前面的理论,如果机构是镜面机构,在输入转速恒定的情况下,则输出转速就是恒定的,在图2-10中,在输入转速恒定为90°/s时,其输出转速是周期变化的。后来经模型修改,将原模型改为完全对称结构,满足镜面机构的条件,重新进行仿真,得出的结果是输入转速同输出转速完全相等。这从正反两面说明了前面理论的正确性,同时也说明要想得到等角速传动并不是一件简单的事。不过本次证明只是对一种形式机构而言,有关其它的机构形式,还需要进一步的探索。
上一页
下一页





