2.2.3 等角速回转连杆机构结论
由上面的分析可知，对于非镜面对称的RPSPR机构，不可能具有等角速回转的特性。
所有的机构中，连杆机构仅占一部分，镜面机构又仅占连杆机构的一部分，即使我们证明了上述理论的正确性，所研究的内容也仅占整个机构的很小的一部分，这方面的理论还很不完善，需要进一步地研究。
2.3 等角速万向联轴器的理论及产品
关于等角速万向联轴器到目前已形成了三种理论，和大量的相关产品。
已创建的等角速联轴器的等角速传动理论如下：
双十字轴万向联轴器实现等角速传动的理论；
传力点位于两轴交角平分面内的等角速传动理论（定心式理论）；
瞬时滑动——转动轴理论（非定心式理论）。
2.3.1 双联十字轴等角速传动理论及其产品
2.3.1.1 双联十字轴等角速传动理论
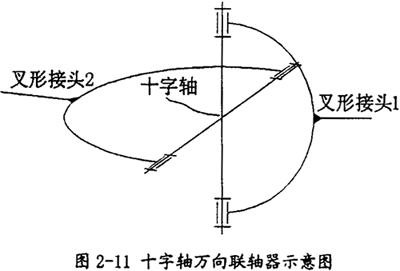
十字轴万向联轴器的基本结构如图2-11所示，它是由两个在轴上的叉形接头1、2和一个十字轴组成，因为叉形接头和十字轴是铰接的，因此允许被联接两轴有较大的角偏斜，但两轴不在同一轴线上时，主动轴等速运动，从动轴将在某一范围内作周期的变速运动，即两轴不同步。
单联万向联轴器的运动关系：
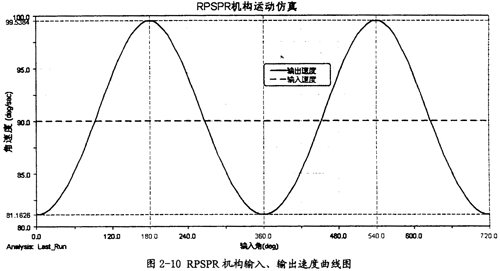
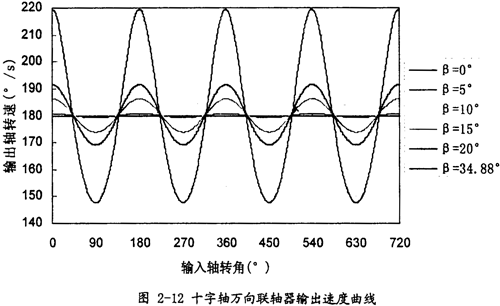
十字轴万向联轴器的机构实际上是球面四连杆机构，它的空间运动关系早已解析出。当输入、输出两轴线的夹角为β输入轴转角фi转速ωi，输出轴转角фo，转速ωo，则它们的位移关系式为：tgфi=tgф0cosβ，速度关系式为：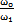
=
，曲线图如图2-12（此图的目的主要是为了后面的验证所示。
双联十字轴万向联轴器等角速传动原理：
现假设有两个十字轴万向联轴器，按图2-13或图2-14联接在一起，主动轴同从动轴与中间轴之间的夹角分别为αl、α2，当主动轴转过ф1角，中间轴转过ф0角，从动轴转过ф2角，则由上面的位移关系，有如下式子：
对第一个万向联轴器有：tgф0=tgф1cosα1
对第二个万向联轴器有：tgф0=tgф2cosα2
于是可得：tg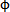
1cosa1 =tg2cosa2，若要等角速，即：2=1则有：α1= α2
这样就得到了双联十字轴万向联轴器等角速传动时的两种空间布置形式，也就是图2-13和图2-14所示的两种方式。
将双联十字轴万向联轴器的这两种布置形式，用文字描述如下：
当两个十字轴万向联轴器配合使用，则有可能实现等速传动，只需满足如下条件：
传动轴、主动轴和从动轴三轴应在同一平面内：
传动轴两端叉形接头的叉口应位于同一平面内；
传动轴与主、从动轴之间的轴间角应相等。
这也是双联十字轴万向联轴器等角速传动的原理。从这一理论可知，它是面向于一种具体的联轴器上的理论，只是针对十字轴万向联轴器，因而适用范围较窄。
在这样的理论指导下，人们制作了图2-15所示的双联十字轴等角速万向联轴器。它的关键结构就是中间的轭机构，它保证了两轴同轭（相当于中间轴）的夹角始终相等，从而实现等角速传动。
2.3.1.2 双联十字轴等角速传动理论的产品
2.3.1.2.1 环叉式万向联轴器
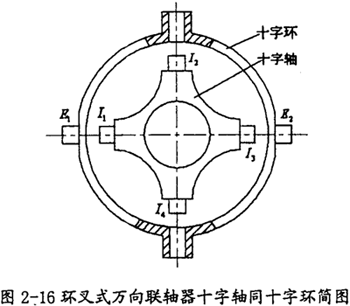
在双联十字轴等角速万向联轴器理论的指导下，人们将中间的传动轴缩短为零，而将两十字轴相应变为十字轴和十字环的结构（如图2-16所示），于是就产生了环叉式等角速万向联轴器。其结构原理简图如图2-17所示。
在这样的理论指导下，人们制作了图2-15所示的双联十字轴等角速万向联轴器。它的关键结构就是中间的轭机构，它保证了两轴同轭（相当于中间轴）的夹角始终相等，从而实现等角速传动。
环叉式万向联轴器的结构原理：
环叉式万向联轴器是在双联式万向联轴器的基础上发展而成的。取消中间轴，使其两端的十字轴在几何上重合为一个平面，从而保证了理论上的等速传动。为避免两十字轴重叠时，轴实体发生干涉，将其中一个十字轴实体改为虚体——变形为一个中空的圆环，称为“十字环”。十字环上开有两对中心线互相垂直的销孔和短销轴，实质上构成虚体十字轴，同样起十字轴作用，使虚体和实体两个十字轴在几何上能重叠为一个平面。由于万向联轴器具有“环”和“叉”的结构特征，“环叉式万向联轴器”由此得名。
当环叉式万向联轴器传递转矩时，转矩由叉轴l（主动叉）传到十字轴，再传到十字环及叉轴2（从动叉）。此机构虽具备动力传递功能，但要满足其匀速运动特性，尚须增加一套分度装置，为此将球笼式万向联轴器的杠杆式分度机构移置到环叉式万向联轴器上来，这就达到了万向联轴器传力点的运动平面是主、从动轴的角平分面的等速传动条件。
环叉式万向联轴器的特点：
a.静态传动等速性近似球笼式万向联轴器；
b.最大工作夹角、最大转角差均达到了球笼式万向联轴器的水平；
c.负荷能力、使用寿命、加工精度等同于传统的双联十字轴万向联轴器，同时具有十字轴万向联轴器的其它优点，如：加工制造容易、成本低廉、价格便宜等等；
d.结构紧凑，能满足前轮驱动轿车结构布置的要求，具有广阔的应用前景。
上一页
下一页
