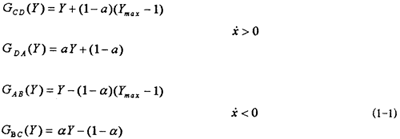第一章 绪 论
1-1 问题的提出
为了适应船舶防振抗冲降噪的要求,拟在主机和推进轴系之间使用一种新型的大挠度高弹性联轴器。
这种新型联轴器以钢丝绳作为弹性元件,恢复力包括钢丝绳间的摩擦、滑移、挤压力等,具有变刚度,变阻尼的迟滞非线性特性,本构关系非常复杂,表现出与变形历史有关的迟滞非线性。它能承受大变形,具有缓冲的能力,当变形足够大时。钢丝绳各股之间发生摩擦,因而具有干摩擦阻尼,能保证在较宽的频带内吸振,而在小变形时,钢丝绳各股之间不发生滑移,这时具有高刚度和高稳定性,由这种弹性构件制成的联轴器不仅能补偿三维大偏移,而且集隔振器,缓冲器和吸振器功能于一身,具有改善推进轴系振动的作用。
这种联轴器内部机理复杂,在开发和应用前,有必要对以下重要问题进行研究:
1.钢丝绳联轴器动刚度和阻尼与振动参数的关系,联轴器恢复力与动刚度和阻尼的关系。
2.含有钢丝绳联轴器的轴系稳态响应计算方法以及联轴器对轴系振动特性的影响。
本文将以这些问题作为基本研究内容,建立一套实用的分析、计算、试验方法,并研制相应的计算机软件。
1-2 综述
一、概述
对非线性元件变刚度和变阻尼特性这一现象,在二次大战前后就已经注意到并进行了一系列研究。早在30年代,Den Hartog对干摩擦阻尼单自由度系统稳态响应进行了研究,他指出对共振,仅在激励力较窄的幅度范围内能用干摩擦控制振幅,如激励力小于摩擦力则不发生滑动,如果激励力大于4/π倍摩擦力,则又控制不了共振。因而多年来人们一直认为用纯干摩擦控制共振的成效不大。但是干摩擦是存在于结构结点和两接触面的一个固有特性,结构在振动时90%的能量耗散集中于结点及接触面上,因此利用结点摩擦耗能减振是减振研究和应用的一个重要方面,许多研究成果已写进了专著,50年代初就曾利用汽轮机叶片根部摩擦滑动控制叶片共振。由于干摩擦机理的复杂性,利用干摩擦阻尼减振的应用不多。70年代中期前,一些非线性抑振的研究主要偏重于理论分析,非线性元件结构形式也较为复杂,非线性抑振技术主要用于一些特殊场合,例如Miodlin分析了非线性刚度对缓冲效果的影响,指出了硬化刚度的缓冲器受冲击时储能小,因而缓冲的效果不如线性缓冲器。Roberson从理论上证明刚度软化的非线性吸振器具有比线性吸振器更宽的工作频带,这些研究结论为发展非线性抑振器提供了重要理论依据。
进入七十年代中后期以来,非线性振动的研究和实际应用方才大为发展,研制了干摩擦隔振器用于高层建筑的隔振。近年来发展了弹塑性耗能器、摩擦闸、限位器、铅芯橡胶减振器等非线性振动控制元件与技术。在抗震结构中,利用干摩擦阻尼耗能原理制成的非线性弹性元件已广泛应用。近年来,利用滑动隔振结构配以浮升限制器来控制振动响应也取得较大成果。
七十年代末,八十年代初发展起来的钢丝绳隔振器是利用钢丝绳股之间的干摩擦提供阻尼的一种非线性隔振器,它能够承受大变形,吸收大的冲击能量,又具有高阻尼,能在较宽频带内隔振,此外还具有耐高低温、抗油污、耐腐蚀等优点,现已广泛地应用于航空、航天、船舶、交通运输、结构和建筑物等领域。
由于弹塑性耗能器、摩擦闸、钢丝绳隔振器这类隔减振器材均具有非线性迟滞特性,本构关系十分复杂,因此在研制过程中不得不借助试验反复修改设计,为了有效地预估动态响应,改进抑振效果,迫切需要一套简便,切实可行的方法来取代传统的经验和试凑设计。这就导致了非线性迟滞特性系统建模问题和系统辩识问题。
二.非线性迟滞系统的建模
对于非线性迟滞系统的建模,到目前为止,最具代表性的数学模型有三种:它们是双线性恢复力模型;一阶非线性微分方程模型和迹法模型。
1.双线性模型
双线性模型是非线性迟滞系统模型中最简单的一种,而且也是最为久远的模型,对于它的初始机理研究最早可追溯到三十年代的Deo Hartog,他在研究干摩擦时提出了干磨擦的理想模型,他认为在一个具有干摩擦面的单自由度系统中,干摩擦力随相对滑移位移的关系可用一矩形来表示,如图1-1所示。当该系统受到外力激励发生运动时,干摩擦力总是与运动速度反向而且阻碍运动,进而耗损系统的能量,从时域的角度看,干摩擦力的波形为矩形波,Den Hartog还按能量耗散相等原理,把理想干摩擦等效成粘性阻尼。实际上干摩擦交界面,在外力小于摩擦力时,两边就有变形,随着外力的增加,此变形随之增大,这是因为交界面两边的物质有一定的弹性。即使两边有较大的滑移时,交界面上的干摩擦力仍然不是常数,而是随振幅的增大而缓慢上升的。Earlestes等人对此作了描述,认为一旦交界面有了滑移,干摩擦的线性力不是常数(4Ffπ),而是与相对位移X有关,从Ff变到4Ff/π,表达式为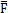 = Ff+δXm,式中δ为一常数,由实验确定,在等效线性力相位上,仍认为等效摩擦力总是与相对速度差180°。
= Ff+δXm,式中δ为一常数,由实验确定,在等效线性力相位上,仍认为等效摩擦力总是与相对速度差180°。
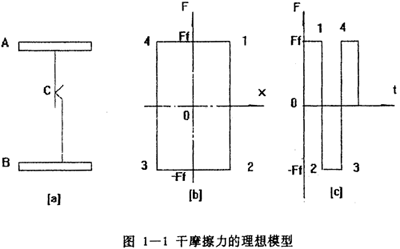
在对迟滞系统的研究中,用双线性模型可以近似描述迟滞回线,双线性模型如图1-2(a)所示,双线性恢复力模型可以由两个线性刚度Ka和Kb以及临界滑移力Fy来描述。
对图1-2(a)所示的双线性迟滞回线进行分解可得图1-2中的(b),(c)两个图形,即双线性恢复力可分解为线性弹性恢复力和迟滞阻尼力两部分。由迟滞部分的(c)图可以看到作用于AC间的外力小于摩擦力Ff时,AB间干摩擦接触面之间无相对滑移,而只有线性弹性变形(沿oa),此时系统呈线性特性,当在外力作用下,BC间弹性力达到干摩擦力Ff时,AB间的接触面开始产生相对滑移,直至速度为零并改变方向(沿al)。当外力改变方向后,BC间的弹性力由Ff逐渐减少至零,再线性增至-Ff(沿12),这时AB间的接触面再次滑移,直至速度为零并改变方向(沿23)。如此周而复始就形成了迟滞回线。对于双线性恢复力模型,需要辩识的参数有三个,即ka,kb和临界滑移力Fy。
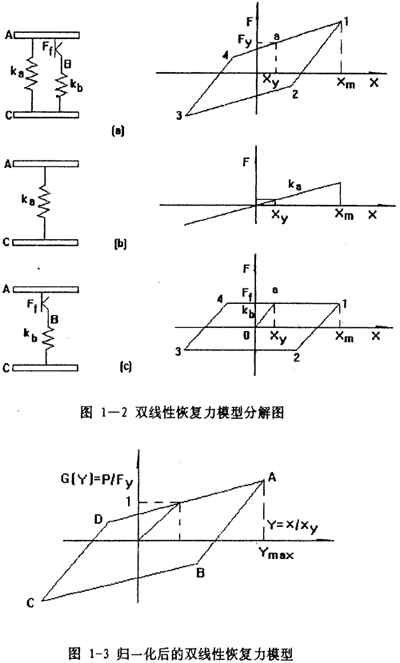
双线性恢复力模型也可以用无量纲参数α=Kb/Kα,β=F/Fy来描述,式中F为激励力,在这种情况下,迟滞回线如图1-3所示。归一化后的双线性回线,方程由式(1-1)表示。
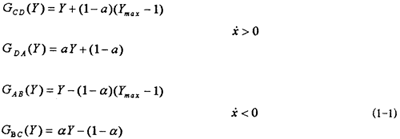
2.一阶非线性微分方程模型
Jenning,Iwan,和Bouc分别提出了平滑变化的迟滞模型。其中Bouc提出的模型为:
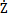 =A
=A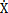 -a|
-a|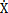 |Z-β
|Z-β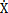 |Z| (1-2)
|Z| (1-2)
式中Z为迟滞恢复力,X为位移,A,α,β分别为参数,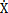 为速度。这是一个迟滞恢复力为一阶微分方程的模型。
为速度。这是一个迟滞恢复力为一阶微分方程的模型。
Wen等人先后对这个微分方程进行了发展和推广,发展后的微分方程形式为:

由此方程描述的迟滞回线形状和大小由A,α,β等三个参数控制,而曲线的光滑程度由n控制,因此通过调节这些参数的数值,可以得到大小和形状各异的迟滞曲线。为了使这些迟滞模型也能包含双线性模型,Yar和Hammond对上述方程进行了修改:
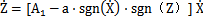 (1-5)
(1-5)
式中A1=A-β,为了全面包含双线性迟滞系统,进一步修改为:
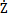 ={A-a·sgn(
={A-a·sgn(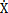 )·sgn[Z-β·sgn(
)·sgn[Z-β·sgn(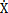 )]}
)]}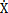 (1-6)
(1-6)
由以上各种形式的一阶微分方程可知,迟滞恢复力Z与位移x的关系很不直观,各参数的物理意义不明确,各表达式反映不出迟滞恢复力与弹性恢复力和阻尼力之间的明确关系。这类模型多用于迟滞系统的随机响应分析中。近年来,有人利用这种模型来研究机床切削颤振,合理地分析和解释了以往颤振理论无法解释的现象。
上一页
下一页