3.迹法模型
Badrakan提出迹法模型，并在1987年用迹法模型研究了在双线性迟滞恢复力作用下系统的特性，得到了具有双线性迟滞恢复力的系统在高斯分布稳态白噪声激励作用下系统的响应特性，迹法中迟滞恢复力可以表示为：
f（y，
）=g（y）+h（y）·sgn（） (1-7)
式中f（y，）恢复力是位移和速度符号的函数，g（y）为迟滞回线上下边f+和f-的平均值函数：
g（y）=（f++f-）/2 （1-8）
而h（y）是
h（y）=（f+-f-）/2 （1-9）
于是有
f+= g（y）+ h（y）
f-=g（y）- h（y） （1-10）
由h（y）·sgn（）定义的回线由一个椭圆来近似，该椭圆的面积和幅度与回线相等，表示一个等效的粘性阻尼，由此可知，在迹法中迟滞回线用两项来等效，一项是回线的迹线，另一项是等效的粘性阻尼。Badrakan后来又进一步提出迟滞回线的迹线可用一条多项式曲线来近似。基于平均和等效原理的迹法是一种建立小位移迟滞系统数学模型的实用方法。近年KO等人用迹法对钢丝绳振动隔离器受剪切时的迟滞特性进行了实验研究，将弹性恢复力用三个阶次的非线性弹簧刚度与位移的五次方函数关系表示：
F1= F1（x，A）=K1（A）x+K2（A）x3+K3（A）x5 （1-11）
阻尼力用等效粘性阻尼表示：
F2=F2（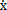
，A，ω）=C（A，ω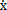） （1-12）
在进行K1（A），K2（A)，K3（A）的参数辩识时，用直接拟合平均初始刚度的所有值而获得K1（A）与振幅A的关系式；用两个特殊值F1（x，A）|x=A和dF1／dx|x=A联立方程求解来获得K2（A)，K3（A）与振幅A的关系式。由此方法得到的数学模型简单、明了，各参数的物理意义明确，较好地反映研究对象的内部机理。但是，由于实际的迟滞系统结构各不相同，内部机理也各异，当系统的非线性表现得更为强烈，须用更高阶非线性弹簧刚度来描述时，方法就不行了，因为它只能用特殊关系来获得K2（A)，K3（A）与振幅的关系式，而不能获得更高阶的刚度。
除了以上三种典型的迟滞力模型外，描述力和位移迟滞关系的模型还有Dayideokov模型，描述迟滞回线两个分支的表达式为:
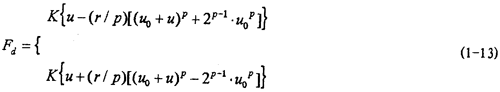
式中u0为位移幅值，r，P为参数，u为位移，Fd为恢复力。Pisareoko、Vinogradov等人用这一模型研究非线性迟滞特性系统的振动。另外还有Ramberg-Osgood模型,Menegotto-Pinto模型和三折线模型等。
综上所述可知，描述非线性迟滞特性的数学模型都是针对某些迟滞系统提出的，它们各有不同的应用场合，并且有各自不同的优缺点。对于双线性模型来说，它形式简单需辩识的参数少，物理意义清楚，但它将系统处理成两个线性刚度系数，无法描述强非线性高阶刚度系数的影响，对阻尼仅处理为干摩擦阻尼，也不足以描述阻尼的复杂情况一阶微分方程模型可以描述大小不同，形状各异的迟滞回线，但它各参数的物理意义不明确，表达式以导数或微分形式出现不利于各参数的辩识，而且恢复力中的弹性力和阻尼力表现形式不显现。迹法模型以及在此基础上KO等建立的模型，物理意义明确，表达式简单明了，但前者只能描述迟滞恢复力与位移和速度的关系，而不能全面揭示迟滞恢复力与各振动参数的关系，后者由于辩识高次非线性弹簧刚度的能力限制，使它的应用范围受到了制约。由此可见，目前尚无一种十分理想的模型可以用来准确地描述非线性迟滞系统的动力特性。因此，在研究钢丝绳联轴器非线性迟滞特性时，汲取前人研究成果中的合理部分，建立一个能较好的描述联轴器非线性迟滞动力特性的数学模型将是本文研究工作之一。
三.非线性迟滞系统的参数辨识
数学模型建立以后，下一步工作就是辨识数学模型中的未知参数。已有的研究大多是关于线性系统的，关于非线性迟滞特性系统的参数辨识工作做得不多。只是最近几年来方才有些发展。由于非线性迟滞系统问题的双值性和非线性，成为非线性系统参数辨识的前沿课题。
1.非线性迟滞系统参数的可辨识性问题
非线性迟滞系统参数辨识的研究工作发展的如此缓慢的主要原因之一是系统恢复力是一个位移的双值非线性函数。在参数辨识过程中首先遇到的问题是非线性迟滞系统数学模型中的参数是否是可辨识的，因为大多数参数辨识技术基础的假设是回归函数的解析性，然而，对于非线性迟滞系统来说，回归函数是双值和非解析的，这就导致了非线性迟滞系统是否是可辨识的问题。
Grewal等人通过考察非线性系统对应的一个线性化局部系统能识性来研究非线性系统的可辨识性。
Aodronikou等人以单自由度的双线性迟滞模型为例，研究了迟滞系统的可辨识性问题。他们根据文献的提法，分为两个步骤：第一步用等效的单值非线性系统代替实际的双值双线性系统；第二步研究等效后单值非线性系统的能识性，并考察了两个系统能识性的关系。该文献指出，假定两个系统都受到足够小的激励，两个系统以相同幅值和频率谐振，则原始非线性迟滞系统是可辨识的。
研究非线性迟滞系统可辨识性问题的文献极少，这方面的工作有待进一步研究，以期从数学上解决非线性迟滞系统是否是可辨识的问题。
2.非线性迟滞系统参数辨识
尽管问题还没有从数学上解决，但是，由于实际工作的需要，还是在非线性迟滞系统的参数辨识方面作了一些研究。
Kohr曾提出一种非线性参数辨识方法，后来Hoborock和Kohr在此基础上，把方程误差技术与优化方法中的最陡下降判断算法应用于未知参数的辨识，但是这种方法只能用于识别一个非线性未知参数项的系统。Sprague和Kohr进一步采用分段连续函数展开的技术成功地辨识了许多工程上非线性单值函数的参数。Seitoglu和Klein在文献的基础上，提出了用于辨识一类非线性函数（其中包括有多值和记忆（即迟滞）特性的函数）的技术。这种方法要求非线性迟滞系统能表示为一系列常微分方程，并且限于分段连续的非线性时不变，集中参数方程。
Distefano和Rath把最小二乘法应用于双线性恢复力迟滞模型，有三个未知参数，作为一个优化滤波问题求解。文献指出，对不同的力函数和不同的初始条件同时辨识三个参数的尝试是不成功的。
Andronikou,Bekey和Masri在文献的基础上应用自适应随机搜索算法来识别具有三个未知参数的双线性恢复力非线性迟滞系统，输人为正弦激励，这种方法要求激励输人信号是简谐的并且有足够大的幅值，但这种方法的收敛速度较慢。
胡海岩和李岳蜂用双折线模型（即双线性模型的特殊情况，如图1-2(c)所示模型）来近似描述非线性减振器的迟滞恢复力，在大变形前提下构造了单值支的解析展开，把非线性参数辨识简化成展开系数及无迟滞恢复力模型参数的线性估计，在此基础上建立了两种参数辨识方法，这样在正弦激励下通过一次试验即可获得建模所需的全部物理参数。
最近，陈乃立和童忠钫提出了一种将双折线非线性迟滞系统的参数进行分离识别的方法，将迟滞振动系统的非线性恢复力分离成迟滞恢复力、仅与位移有关的非迟滞恢复力和仅与速度有关的非迟滞恢复力等三部分来分别加以识别，它计算量小，具有较好的坑噪声能力。
Lo,Yar和Hammon提出了用最小二乘优化方法来拟合测量数据，采用的迟滞恢复力模型是一阶徽分方程，他们用数字仿真进行未知参数的估计，结果表明是可行的，但是这种算法未能估计出全部未知参数。
Yar和Hammond就一阶微分方程迟滞恢复力模型的参数估计提出了一种二阶段迭代最小二乘算法，仿真过程和结果表明这种算法在某些情况下不收敛。文献没有明确给出可容许的噪声指标。
Yar和Hammond根据Fokker Plank Kolmogrov方程和高斯牛顿迭代法提出了一种估计微分方程模型未知参数的方法，克服了时域法对差分方程近似的不足，并可防止在模数转换过程中引进误差．他们把这种方法应用于Duffing方程和迟滞系统的参数识别。
提出了由能量积分来分批识别非线性系统参数的新方法，把系统力学模型分为耗能元件和保守元件，利用保守元件不耗能，由此建立仅含耗能元件参数的线性识别方程，以此为基础再利用能量积分建立仅含保守元件参数的线性识别方程。仿真试验表明，此方法简便有效。
综上所述，参数辨识首先要求对非线性迟滞系统特性有一定了解，然后建立系统的数学模型，辨识的目的在于按照选定的估计准则和算法确定出数学模型中表示系统特性的未知参数值。目前，常采用的估计准则有最小二乘原理、极大似然原理、贝叶斯估计原理等，用得最多的是最小二乘原理。所用算法多为各种优化算法，并用数值仿真来检验辨识方法的优劣。
四.非线性迟滞系统的非参数辨识
当对非线性振动系统了解不充分，辨识目标尚不能具体到物理参数时，可以在函数空间里按照一定的误差准则来寻找最佳逼近系统特性的函数。这就是非参数辨识法．这类方法对于一般单值非线性问题效果较好，但对于多值非线性迟滞问题效果结果往往不能令人满意。这是因为对于多值问题，虽然可设恢复力关于相应状态单值光滑，但客观存在的多值性常常使得待逼近的曲面极不光滑，导致偏离实际的估计。另外，这类方法得不到研究者所关心的物理参数。不过，在无法建立系统的数学模型的情况下，非参数辨识方法不失为一种可行的方法。
关于非线性系统的非参数辨识方法的研究近年来很活跃，但是决大多数不能用于非线性迟滞系统。Masrl等人采用chebyshev正交多项式函数族来逼近任意未知非线性恢复力，据称这种方法适用于非线性迟滞恢复力。
近来，提出将迟滞恢复力分离成有记忆恢复力和无记忆恢复力，而无记忆恢复力又分别分离成与速度有关的部分和与位移有关的部分，然后用正交的函数项级数分别去逼近无记忆恢复力的两部分。这是应用非参数识别方法来达到参数识别目的的有益尝试。
五.非线性系统的稳态动力响应分析方法
非线性系统的稳态动力响应分析方法在近几年得到了广泛的研究。一种由Lau等人提出的多简谐频域法，增量谐波平衡法IHB(the incremental harmonicbo1aoce)，已经被成功和广泛地应用于非线性动力系统和有关问题的稳态响应分析。该方法是Newton-Raphson增量法与谐波平衡法的结合，这种方法能很好地处理受到任意周期激励的强非线性系统。
另一种由Ferriet发展起来的GNR法（Galerkin/Newtoa-Raphson）也适用于多谐振的频域解法技术。GRN法和IHB法本质上是等效的。在IHB法中，首先用Newton-Raphson方法来形成一个线性化的增量方程系统，然后用Galerkin方法来获得增量方程的解。在GNR法中，第一步执行Ga1erkin方法以形成一组非线性代数方程组，然后用Newton-Raphson解法来联立求解这组非线性代数方程。这两种基本上等效的方法具有他们各自的特点，因此可以根据实际情况选用。
Liug等人在获得较高阶简谐项时，为了减少计算量，发展了一种快速Ga1erkin方法（FG法），这种方法可以使得IHB法和GNR法的执行更为有效。即在Galerkin方法中引进了快速Fourier变换（FFT）。
近年，Caoron等人提出了一种用于非线性系统稳态响应分析的频率／时间域交替方法（AFT)(alternating frequency/time)。此法在频率域内提供迭代执行程序，但是在每次迭代处，为了计算某些不能在频域解析表达的非线性项的值，它需要从频率域转换到时间域然后再转换回频域。这种方法表明，频率域和时间域之间的信息交换对于分析某些只在频率域内分析很难得到稳态响应的非线性系统是必不可少的。
最近，wong等人用GLM法（Galerkin-Levenberg-Marguardt）对一个基础由钢丝绳隔振器将其与地面隔离的框架结构进行了稳态响应的计算分析和研究。此方法在处理过程中，首先将含有钢丝绳隔振器非线性迟滞恢复力的微分方程用Galerk加方法变换成一组非线性代数方程，然后用LM法迭代计算系统多谐解的各系数，由此求得系统的稳态响应。由于隔振器非线性迟滞恢复力的复杂性，在计算稳态响应的过程中，也采用了类似于AFT法的处理方法，将位移幅值中介变量的频率域信息借助于频率／时间域交替变换来获得。结果表明，这种方法对于计算含有非线性迟滞特性隔离装置的框架结构的稳态响应是有效的。
对于计算转子-轴承系统动力学方法的研究，自七十年代以来，已经有相当大的发展，例如传递矩阵法、有限元法和子结构模态综合法等已得到很大的发展并广泛地应用于原动机一转子一轴承一基础系统的动力分析，然而，在转子-轴承系统动力分析中考虑弹性联轴器影响的研究工作做得很少。在轴系中考虑弹性联轴器对系统动力影响的研究工作的难点在于，一是建立较为精确的弹性联轴器模型有困难，特别是当弹性联轴器的动力特性呈非线性特征时尤其如此，二是计算方法的问题，特别是轴系中考虑弹性联轴器的非线性特性时，计算更是困难。
本文拟在建立起钢丝绳联轴器数学模型的基础上，研究含有这种联轴器的轴系系统，发展一种能计算这种轴系稳态响应的分析计算方法，由此考察钢丝绳联轴器动力特性对轴系响应的影响。将这一方面的研究工作向前推进一步。
1-3 本文研究工作简介
本文以大挠度钢丝绳联轴器以及含有这种联轴器的轴系为研究对象，在分析和借鉴前人研究非线性迟滞动力系统建模理论和系统辨识方法的基础上，根据本领域最新研究发展的新动向，来研究钢丝绳联轴器自身的动力特性以及含有该联轴器轴系的振动特性。试图通过理论分析和试验研究，为开发和应用钢丝绳联轴器于船舶推进轴系，建立一套比较完整的分析，计算和试验方法。
主要工作概括如下：
1.在广泛查阅国内外有关文献的基础上，较全面地掌握了该领域的发展动态，为探讨大挠度钢丝绳联轴器及其轴系的动力特性莫定了基础；
2.探索了大挠度钢丝绳联轴器的动态试验方法，提出了一种激励大位移振动的新方法，克服了传统激振方法不能同时使频率、振幅和激励力达到一定的要求的困难，为研究大挠度钢丝绳联轴器的动力特性解决了大位移振动试验的难题；
3.提出了用于具有非线性迟滞特性联轴器动力特性研究的拟合分解法，以此为基础构造了大挠度钢丝绳联轴器物理参数辨识方法，并研制了相应的软件，解决了大挠度钢丝绳联轴器的建模问题；
4.对一类在方程中刚度和阻尼与振幅有关的强非线性自治系统，提出了求解其稳态响应的近似解析法---频闪-谐波平衡法，由此可以求出系统产生主共振解和次谐共振解的条件，为防止共振提供了理论依据，数字仿真结果证实了理论的正确性；
5.提出了一种用于含钢丝绳联轴器轴系稳态响应计算的组合算法并研制了软件；试验结果支持了组合算法的正确性；
6.对钢丝绳联轴器的研究前景做了展望。
上一页
下一页
