3 共轭曲面的数字化方法实现与计算
3.1 引言
两个相互运动且保持相切接触的曲面互为共轭曲面。共轭曲面解问题是在已知一个由解析方程式表达或一系列离散数字坐标值表达的曲面和已知两个曲面的共轭运动的前提下,求解另一个曲面的问题,在机械设计和机械加工中有着广泛的用途,诸如工具曲面,轧钢辊面以及齿轮齿面设计、凸轮轮廓设计、机构的运动分析与综合、加工仿真等众多领域。基于MATLAB的数学化共轭曲面求解及仿真研究,旨在充分利用MATLAB强大硬捷的数学运算和图形显示功能[84-92],将共轭曲面求解中复杂的推导和计算过程由MATLAB编程实现,并增强计算机对于各种已知曲面(包括解析曲面和数字化曲面)和各种曲面共轭运动的适应能力,以减轻工程人员的负担,并增强计算的精度。
3.2 基于MATLAB的数字化共轭曲面求解实现
3.2.1 求解数字模型
用MATLAB解决数字共轭曲面求解问题,首先要处理已知曲面的数据,把已知曲面变换为适合MATLAB计算的矩阵形式。已知曲面如果由解析表达式表示,则就把解析式离散化为曲面坐标值矩阵;如果由不规则离散坐标值表达,则应把不规则离散坐标值重构为规则坐标值矩阵。
用一维数组与单个点的运动轨迹对应,用二维数组与曲面对应,用三维数组与曲面族对应,使得共轭曲面求解中所用到的各个要素,都由适合MATLAB计算的形式来表达。
共轭曲面求解的关键是求曲面上一点的法矢N和点的运动轨迹的切矢v12,基于MATLAB的数字化共轭曲面求解也是围绕这两个关键量展开。
根据以上论述的曲面共轭条件和MATLAB的运算特点,构造如下的共轭曲面求解数学模型:

式(3-1)中第一式表示曲面Σ1由坐标系S1变换到坐标系S2所形成的曲面族,Xmatrix,Ymatrix,Zmatrix分别表示曲面族中各点在x,y,z坐标方向上的坐标值;第二式中的,NXt,NYt,NZt表示曲面Σ1在点(u,v)对应于t的相对法矢分量,DXt,DYt,DZt表示点(u,v)运动轨迹对应于t的相对切矢分量。
3.2.2 求解模型算法
(1)对规则化后的坐标值进行坐标变换,求出已知曲面Σ1在坐标系S2中对应于序列t的位置坐标和曲面各点的法矢,分别得到对应于曲面族坐标值的三个三维数组Xmatrix,Ymatrix,Zmatrix和对应于曲面族中曲面法向量的三个三维数组NXmatrix,NYmatrix,NZmatrix。三维数组的各维分别对应不同的u,v,t;
(2)给定uj值;
(3)给定vk值;
(4)分别将三维数组Xmatrix,Ymatrix,Zmatrix沿点(uj,vk)运动方向进行一维抽取,得到三个一维数组Xt,Yt,Zt,它们表示点(uj,vk)对应序列t的坐标值,也即点(uj,vk)的离散运动轨迹。将Xt,Yt,Zt分别对应于序列t进行三次样条曲线插值,然后分别求导,得到三个一维数组DXt,DYt,DZt,它们表示点(uj,vk)的运动轨迹对应于序列t的相对切矢分量;
(5)分别将三维数组NXmatrix,NYmatrix,NZmatrix沿点(uj,vk)运动方向进行一维抽取,得到三个一维数组:NXt,NYt,NZt,它们表示曲面Σ1在点(uj,vk)对应于序列t的相对法矢分量;
(6)取ψ(uj,vk,t)=NXt·DXt+NYt·DYt+NZt·DZt,那么ψ(uj,vk,t)是一维数组,它表示点(uj,vk)对应序列t的ψ(u,v,t)的值,然后利用tt=spline(ψ,t,0)实现优化的功能,得到ψ(uj,vk,t)=0时t的值tt;
(7)利用计算分段多项式的方法求出点(uj,vk)对应于tt的坐标值Xtt,Ytt,Ztt,然后将它们分别赋给数组元素Xcon(uj,vk),Ycon(uj,vk),Zcon(uj,vk);
(8)vk←vk+△v,转至(3),直到v方向计算完毕;
(9)uj←uj+△u,转至(2),直到u方向计算完毕。
如果点(uj,vk)在整个t的运动过程中都没有使ψ(uj,vk,t)=0,则可判断此点没有参与共轭,在共轭曲面的求解中剔除该点;如果有超过一次的使ψ(uj,vk,t)=0,则可判断此点在整个运动过程中多次参与了共轭,这种已知点和所求共轭点“一对多”的映射会导致程序判断的紊乱,对于这种情况,可利用使t自动分段和递归调用共轭求解函数的方法来处理,直至在每一个t的分段中(uj,vk)参与共轭的次数不超过一次。
通过上述计算,最后得到三个二维数组Xcon(u,v),Ycon(u,v),Zcon(u,v),这就是共轭曲面求解的结果,它们表示与曲面Σ1相共轭的数字曲面Σ2的坐标值。在此基础上,调用MATLAB的绘图命令可以显示出共轭曲面的图形。
3.2.3 算法实现
根据上述求解模型与算法,编制出基于MATLAB共轭曲面求解流程图如图3-1所示。

在图3-1中,输入的运动和相对位置参数:
t——两曲面作共轭运动时的运动参数;
ω1,ω2——已知曲面Σ1和共轭曲面Σ2的自转角速度(1/s);
v——Σ1在Σ2轴线方向的运动速度(cm/s);
d——z1轴与z2轴的距离(cm);
θ——z1轴与z2轴的交角(°)。
3.3 数字化共轭曲面求解实例计算
3.3.1 任意曲面的共轭求解
已知一数字化曲面(如图3-2所示),曲面上有21×11个规则网格节点,这些网格节点坐标值的X矩阵、Y矩阵、Z矩阵分别如表3-1、表3-2、表3-3所示。
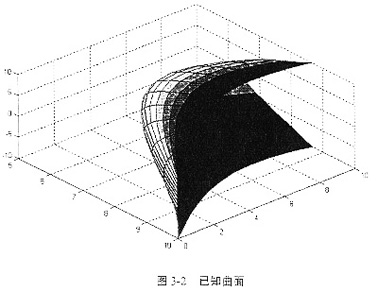
表3-1 已知曲面节点坐标值X矩阵
| |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
| 1 |
10.0000 |
9.6358 |
9.2931 |
8.9914 |
8.7461 |
8.5675 |
8.4600 |
8.4224 |
8.4482 |
8.5271 |
8.6466 |
| 2 |
10.0000 |
9.5596 |
9.1452 |
8.7803 |
8.4837 |
8.2677 |
8.1378 |
8.0923 |
8.1234 |
8.2189 |
8.3635 |
| 3 |
10.0000 |
9.4780 |
8.9868 |
8.5543 |
8.2027 |
7.9467 |
7.7927 |
7.7388 |
7.7757 |
7.8889 |
8.0602 |
| 4 |
10.0000 |
9.3935 |
8.8228 |
8.3203 |
7.9118 |
7.6144 |
7.4355 |
7.3728 |
7.4157 |
7.5472 |
7.7463 |
| 5 |
10.0000 |
9.3093 |
8.6594 |
8.0871 |
7.6219 |
7.2832 |
7.0795 |
7.0081 |
7.0570 |
7.2067 |
7.4334 |
| 6 |
10.0000 |
9.2289 |
8.5035 |
7.8647 |
7.3454 |
6.9673 |
6.7399 |
6.6602 |
6.7148 |
6.8819 |
7.1350 |
| 7 |
10.0000 |
9.1563 |
8.3625 |
7.6636 |
7.0954 |
6.6817 |
6.4329 |
6.3457 |
6.4054 |
6.5883 |
6.8651 |
| 8 |
10.0000 |
9.0952 |
8.2438 |
7.4942 |
6.8848 |
6.4411 |
6.1742 |
6.0807 |
6.1447 |
6.3409 |
6.6378 |
| 9 |
10.0000 |
9.0488 |
8.1538 |
7.3657 |
6.7251 |
6.2587 |
5.9781 |
5.8798 |
5.9471 |
6.1533 |
6.4655 |
| 10 |
10.0000 |
9.0198 |
8.0975 |
7.2855 |
6.6253 |
6.1447 |
5.8556 |
5.7543 |
5.8236 |
6.0361 |
6.3578 |
| 11 |
10.0000 |
9.0100 |
8.0784 |
7.2582 |
6.5914 |
6.1060 |
5.8139 |
5.7116 |
5.7817 |
5.9963 |
6.3212 |
| 12 |
10.0000 |
9.0198 |
8.0975 |
7.2855 |
6.6253 |
6.1447 |
5.8556 |
5.7543 |
5.8236 |
6.0361 |
6.3578 |
| 13 |
10.0000 |
9.0488 |
8.1538 |
7.3657 |
6.7251 |
6.2587 |
5.9781 |
5.8798 |
5.9471 |
6.1533 |
6.4655 |
| 14 |
10.0000 |
9.0952 |
8.2438 |
7.4942 |
6.8848 |
6.4411 |
6.1742 |
6.0807 |
6.1447 |
6.3409 |
6.6378 |
| 15 |
10.0000 |
9.1563 |
8.3625 |
7.6636 |
7.0954 |
6.6817 |
6.4329 |
6.3457 |
6.4054 |
6.5883 |
6.8651 |
| 16 |
10.0000 |
9.2289 |
8.5035 |
7.8647 |
7.3454 |
6.9673 |
6.7399 |
6.6602 |
6.7148 |
6.8819 |
7.1350 |
| 17 |
10.0000 |
9.3093 |
8.6594 |
8.0871 |
7.6219 |
7.2832 |
7.0795 |
7.0081 |
7.0570 |
7.2067 |
7.4334 |
| 18 |
10.0000 |
9.3935 |
8.8228 |
8.3203 |
7.9118 |
7.6144 |
7.4355 |
7.3728 |
7.4157 |
7.5472 |
7.7463 |
| 19 |
10.0000 |
9.4780 |
8.9868 |
8.5543 |
8.2027 |
7.9467 |
7.7927 |
7.7388 |
7.7757 |
7.8889 |
8.0602 |
| 20 |
10.0000 |
9.5596 |
9.1452 |
8.7803 |
8.4837 |
8.2677 |
8.1378 |
8.0923 |
8.1234 |
8.2189 |
8.3635 |
| 21 |
10.0000 |
9.6358 |
9.2931 |
8.9914 |
8.7461 |
8.5675 |
8.4600 |
8.4224 |
8.4482 |
8.5271 |
8.6466 |
表3-2 已知曲面节点坐标值Y矩阵
| |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
| 1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 2 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 3 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 4 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 5 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 6 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 7 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 8 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 9 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 10 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 11 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 12 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 13 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 14 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 15 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 16 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 17 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 18 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 19 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 20 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 21 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
表3-3 已知曲面节点坐标值Z矩阵
| |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
| 1 |
-10 |
-10 |
-10 |
-10 |
-10 |
-10 |
-10 |
-10 |
-10 |
-10 |
-10 |
| 2 |
-9 |
-9 |
-9 |
-9 |
-9 |
-9 |
-9 |
-9 |
-9 |
-9 |
-9 |
| 3 |
-8 |
-8 |
-8 |
-8 |
-8 |
-8 |
-8 |
-8 |
-8 |
-8 |
-8 |
| 4 |
-7 |
-7 |
-7 |
-7 |
-7 |
-7 |
-7 |
-7 |
-7 |
-7 |
-7 |
| 5 |
-6 |
-6 |
-6 |
-6 |
-6 |
-6 |
-6 |
-6 |
-6 |
-6 |
-6 |
| 6 |
-5 |
-5 |
-5 |
-5 |
-5 |
-5 |
-5 |
-5 |
-5 |
-5 |
-5 |
| 7 |
-4 |
-4 |
-4 |
-4 |
-4 |
-4 |
-4 |
-4 |
-4 |
-4 |
-4 |
| 8 |
-3 |
-3 |
-3 |
-3 |
-3 |
-3 |
-3 |
-3 |
-3 |
-3 |
-3 |
| 9 |
-2 |
-2 |
-2 |
-2 |
-2 |
-2 |
-2 |
-2 |
-2 |
-2 |
-2 |
| 10 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
| 11 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 12 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 13 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
| 14 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
| 15 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
| 16 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
| 17 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
| 18 |
7 |
7 |
7 |
7 |
7 |
7 |
7 |
7 |
7 |
7 |
7 |
| 19 |
8 |
8 |
8 |
8 |
8 |
8 |
8 |
8 |
8 |
8 |
8 |
| 20 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
| 21 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
设已知曲面相对于共轭曲面作螺旋运动,t=-π/4:π/20:π/4,ω1=1,ω2=2,v=20,d=20;θ=0。将已知曲面数据和两曲面运动参数输入已编制好的数字化共轭曲面求解程序进行计算,在AMD/K6-233计算机上耗时160s,得到与已知曲面节点对应的共轭曲面各点的坐标值。共轭曲面节点坐标值X矩阵、Y矩阵、Z矩阵分别如表3-4、表3-5、表3-6所示:
表3-4 共轭曲面节点坐标值X矩阵
| |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
| 1 |
7.5009 |
7.3143 |
7.2786 |
7.4834 |
7.8412 |
8.2381 |
8.5695 |
8.7763 |
8.8579 |
8.8579 |
8.7970 |
| 2 |
6.5019 |
6.3129 |
6.3162 |
6.6326 |
7.1478 |
7.7076 |
8.1663 |
8.4408 |
8.5334 |
8.5098 |
8.4057 |
| 3 |
5.3395 |
5.1628 |
5.2208 |
5.6694 |
6.3685 |
7.1204 |
7.7292 |
8.0808 |
8.1815 |
8.1258 |
7.9690 |
| 4 |
4.0790 |
3.9356 |
4.0659 |
4.6614 |
5.5603 |
6.5199 |
7.2873 |
7.7120 |
7.8074 |
7.7052 |
7.4848 |
| 5 |
2.8030 |
2.7145 |
2.9318 |
3.6803 |
4.7815 |
5.9493 |
6.8691 |
7.3509 |
7.4204 |
7.2555 |
6.9620 |
| 6 |
1.5957 |
1.5812 |
1.8974 |
2.7974 |
4.0916 |
5.4523 |
6.5022 |
7.0129 |
7.0302 |
6.7862 |
6.4144 |
| 7 |
0.5308 |
0.6048 |
1.0282 |
2.0738 |
3.5421 |
5.0667 |
6.2096 |
6.7103 |
6.6463 |
6.3101 |
5.8599 |
| 8 |
-0.3379 |
-0.1642 |
0.3712 |
1.5532 |
3.1707 |
4.8189 |
6.0057 |
6.4516 |
6.2789 |
5.8428 |
5.3200 |
| 9 |
-0.9770 |
-0.6949 |
-0.0455 |
1.2614 |
2.9979 |
4.7214 |
5.8955 |
6.2413 |
5.9390 |
5.4028 |
4.8188 |
| 10 |
-1.3672 |
-0.9715 |
-0.2092 |
1.2073 |
3.0279 |
4.7720 |
5.8750 |
6.0817 |
5.6391 |
5.0111 |
4.3812 |
| 11 |
-1.4982 |
-0.9893 |
-0.1192 |
1.3865 |
3.2502 |
4.9566 |
5.9336 |
5.9740 |
5.3938 |
4.6895 |
4.0313 |
| 12 |
-1.3672 |
-0.7504 |
0.2158 |
1.7830 |
3.6419 |
5.2513 |
6.0574 |
5.9210 |
5.2188 |
4.4595 |
3.7911 |
| 13 |
-0.9770 |
-0.2637 |
0.7787 |
2.3707 |
4.1707 |
5.6272 |
6.2324 |
5.9265 |
5.1296 |
4.3402 |
3.6787 |
| 14 |
-0.3379 |
0.4537 |
1.5428 |
3.1137 |
4.7972 |
6.0534 |
6.4463 |
5.9954 |
5.1390 |
4.3456 |
3.7067 |
| 15 |
0.5308 |
1.3732 |
2.4702 |
3.9667 |
5.4780 |
6.5014 |
6.6903 |
6.1315 |
5.2547 |
4.4828 |
3.8802 |
| 16 |
1.5957 |
2.4509 |
3.5106 |
4.8773 |
6.1699 |
6.9472 |
6.9578 |
6.3355 |
5.4770 |
4.7499 |
4.1957 |
| 17 |
2.8030 |
3.6274 |
4.6025 |
5.7898 |
6.8343 |
7.3732 |
7.2440 |
6.6030 |
5.7973 |
5.1348 |
4.6392 |
| 18 |
4.0790 |
4.8304 |
5.6782 |
6.6517 |
7.4412 |
7.7685 |
7.5436 |
6.9240 |
6.1982 |
5.6155 |
5.1865 |
| 19 |
5.3395 |
5.9827 |
6.6738 |
7.4209 |
7.9716 |
8.1275 |
7.8506 |
7.2835 |
6.6555 |
6.1619 |
5.8043 |
| 20 |
6.5019 |
7.0152 |
7.5397 |
8.0713 |
8.4182 |
8.4489 |
8.1573 |
7.6632 |
7.1413 |
6.7396 |
6.4544 |
| 21 |
7.5009 |
7.8840 |
8.2534 |
8.5994 |
8.7858 |
8.7319 |
8.4496 |
8.0343 |
7.6150 |
7.3009 |
7.0848 |
表3-5 共轭曲面节点坐标值Y矩阵
| |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
| 1 |
7.6367 |
7.9193 |
8.0283 |
7.7898 |
7.2266 |
6.3984 |
5.4098 |
4.3939 |
3.4763 |
2.7454 |
2.1232 |
| 2 |
8.8499 |
9.0778 |
9.1245 |
8.7953 |
8.0960 |
7.0790 |
5.8626 |
4.6124 |
3.4894 |
2.6030 |
1.8602 |
| 3 |
9.9609 |
10.1330 |
10.1245 |
9.7238 |
8.9105 |
7.7192 |
6.2783 |
4.7912 |
3.4623 |
2.4255 |
1.5729 |
| 4 |
10.9092 |
11.0248 |
10.9674 |
10.5132 |
9.6077 |
8.2588 |
6.6015 |
4.8826 |
3.3578 |
2.1874 |
1.2473 |
| 5 |
11.6627 |
11.7261 |
11.6285 |
11.1379 |
10.1604 |
8.6713 |
6.8098 |
4.8719 |
3.1708 |
1.8927 |
0.8946 |
| 6 |
12.2197 |
12.2392 |
12.1095 |
11.5938 |
10.5574 |
8.9413 |
6.8891 |
4.7513 |
2.9026 |
1.5498 |
0.5279 |
| 7 |
12.6023 |
12.5878 |
12.4319 |
11.8941 |
10.8016 |
9.0638 |
6.8333 |
4.5207 |
2.5604 |
1.1708 |
0.1603 |
| 8 |
12.8460 |
12.8058 |
12.6259 |
12.0602 |
10.9037 |
9.0417 |
6.6449 |
4.1878 |
2.1576 |
0.7702 |
-0.1966 |
| 9 |
12.9886 |
12.9275 |
12.7207 |
12.1141 |
10.8769 |
8.8831 |
6.3335 |
3.7678 |
1.7119 |
0.3631 |
-0.5341 |
| 10 |
13.0609 |
12.9794 |
12.7381 |
12.0716 |
10.7324 |
8.5985 |
5.9149 |
3.2821 |
1.2438 |
-0.0364 |
-0.8463 |
| 11 |
13.0827 |
12.9766 |
12.6884 |
11.9397 |
10.4769 |
8.2003 |
5.4102 |
2.7560 |
0.7747 |
-0.4152 |
-1.1297 |
| 12 |
13.0609 |
12.9209 |
12.5699 |
11.7161 |
10.1135 |
7.7026 |
4.8448 |
2.2172 |
0.3253 |
-0.7624 |
-1.3817 |
| 13 |
12.9886 |
12.8010 |
12.3696 |
11.3914 |
9.6434 |
7.1224 |
4.2464 |
1.6928 |
-0.0857 |
-1.0683 |
-1.5992 |
| 14 |
12.8460 |
12.5944 |
12.0666 |
10.9526 |
9.0694 |
6.4798 |
3.6438 |
1.2078 |
-0.4422 |
-1.3235 |
-1.7770 |
| 15 |
12.6023 |
12.2711 |
11.6361 |
10.3883 |
8.3995 |
5.7988 |
3.0642 |
0.7831 |
-0.7302 |
-1.5180 |
-1.9067 |
| 16 |
12.2197 |
11.7992 |
11.0564 |
9.6948 |
7.6492 |
5.1057 |
2.5314 |
0.4346 |
-0.9384 |
-1.6412 |
-1.9766 |
| 17 |
11.6627 |
11.1535 |
10.3170 |
8.8807 |
6.8430 |
4.4274 |
2.0640 |
0.1728 |
-1.0584 |
-1.6829 |
-1.9735 |
| 18 |
10.9092 |
10.3252 |
9.4256 |
7.9704 |
6.0122 |
3.7887 |
1.6743 |
0.0023 |
-1.0858 |
-1.6352 |
-1.8851 |
| 19 |
9.9609 |
9.3306 |
8.4122 |
7.0021 |
5.1914 |
3.2101 |
1.3681 |
-0.0779 |
-1.0213 |
-1.4952 |
-1.7046 |
| 20 |
8.8499 |
8.2127 |
7.3260 |
6.0228 |
4.4139 |
2.7059 |
1.1452 |
-0.0746 |
-0.8720 |
-1.2677 |
-1.4334 |
| 21 |
7.6367 |
7.0291 |
6.2151 |
5.0619 |
3.6842 |
2.2577 |
0.9730 |
-0.0255 |
-0.6750 |
-0.9864 |
-1.1011 |
表3-6 共轭曲面节点坐标值Z矩阵
| |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
| 1 |
-7.2914 |
-7.5297 |
-7.8417 |
-8.2902 |
-8.8556 |
-9.5073 |
-10.2070 |
-10.9133 |
-11.5894 |
-12.2084 |
-12.8005 |
| 2 |
-5.7771 |
-6.0372 |
-6.3811 |
-6.8820 |
-7.5185 |
-8.2560 |
-9.0488 |
-9.8463 |
-10.6033 |
-11.2875 |
-11.9355 |
| 3 |
-4.2546 |
-4.5404 |
-4.9192 |
-5.4740 |
-6.1834 |
-7.0097 |
-7.8997 |
-8.7928 |
-9.6338 |
-10.3845 |
-11.0885 |
| 4 |
-2.7460 |
-3.0632 |
-3.4809 |
-4.0916 |
-4.8747 |
-5.7910 |
-6.7802 |
-7.7700 |
-8.6948 |
-9.5100 |
-10.2663 |
| 5 |
-1.2723 |
-1.6258 |
-2.0856 |
-2.7525 |
-3.6081 |
-4.6128 |
-5.6997 |
-6.7843 |
-7.7892 |
-8.6635 |
-9.4658 |
| 6 |
0.1492 |
-0.2442 |
-0.7486 |
-1.4710 |
-2.3965 |
-3.4859 |
-4.6659 |
-5.8396 |
-6.9172 |
-7.8427 |
-8.6820 |
| 7 |
1.5052 |
1.0698 |
0.5196 |
-0.2570 |
-1.2489 |
-2.4174 |
-3.6833 |
-4.9370 |
-6.0770 |
-7.0429 |
-7.9084 |
| 8 |
2.7872 |
2.3090 |
1.7130 |
0.8838 |
-0.1701 |
-1.4107 |
-2.7528 |
-4.0743 |
-5.2635 |
-6.2575 |
-7.1376 |
| 9 |
3.9908 |
3.4700 |
2.8291 |
1.9499 |
0.8389 |
-0.4655 |
-1.8714 |
-3.2461 |
-4.4692 |
-5.4783 |
-6.3612 |
| 10 |
5.1137 |
4.5519 |
3.8681 |
2.9423 |
1.7803 |
0.4224 |
-1.0329 |
-2.4436 |
-3.6846 |
-4.6955 |
-5.5705 |
| 11 |
6.1548 |
5.5549 |
4.8315 |
3.8639 |
2.6587 |
1.2596 |
-0.2280 |
-1.6560 |
-2.8984 |
-3.8989 |
-4.7565 |
| 12 |
7.1137 |
6.4801 |
5.7217 |
4.7188 |
3.4803 |
2.0553 |
0.5547 |
-0.8710 |
-2.0987 |
-3.0778 |
-3.9104 |
| 13 |
7.9908 |
7.3287 |
8.5416 |
5.5120 |
4.2530 |
2.8198 |
1.3273 |
-0.0759 |
-1.2740 |
-2.2223 |
-3.0238 |
| 14 |
8.7872 |
8.1028 |
7.2950 |
6.2495 |
4.9855 |
3.5643 |
2.1023 |
0.7409 |
-0.4140 |
-1.3239 |
-2.0897 |
| 15 |
9.5052 |
8.8060 |
7.9870 |
6.9390 |
5.6879 |
4.3005 |
2.8907 |
1.5889 |
0.4891 |
-0.3760 |
-1.1029 |
| 16 |
10.1492 |
9.4444 |
8.6253 |
7.5900 |
6.3713 |
5.0392 |
3.7018 |
2.4750 |
1.4399 |
0.6247 |
-0.0608 |
| 17 |
10.7277 |
10.0276 |
9.2203 |
8.2142 |
7.0474 |
5.7904 |
4.5421 |
3.4024 |
2.4396 |
1.6780 |
1.0358 |
| 18 |
11.2540 |
10.5688 |
9.7862 |
8.8254 |
7.7281 |
6.5623 |
5.4153 |
4.3707 |
3.4853 |
2.7800 |
2.1821 |
| 19 |
11.7454 |
11.0854 |
10.3393 |
9.4381 |
8.4244 |
7.3609 |
6.3221 |
5.3768 |
4.5711 |
3.9232 |
3.3700 |
| 20 |
12.2229 |
11.5970 |
10.8975 |
10.0666 |
9.1455 |
8.1896 |
7.2609 |
6.4148 |
5.6884 |
5.0975 |
4.5882 |
| 21 |
12.7086 |
12.1216 |
11.4734 |
10.7170 |
9.8902 |
9.0405 |
8.2182 |
7.4673 |
6.8174 |
6.2817 |
5.8154 |
上一页
下一页



