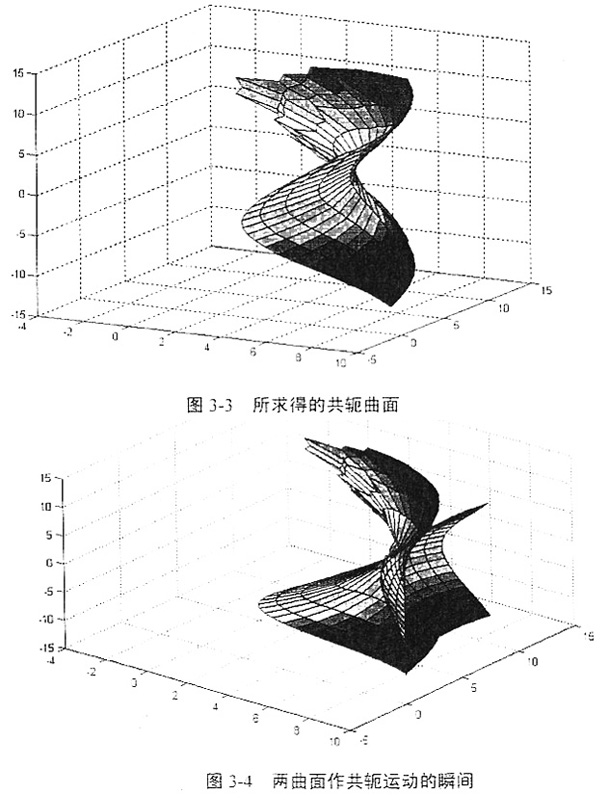
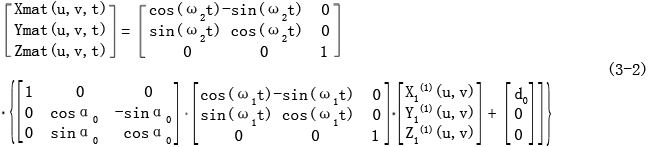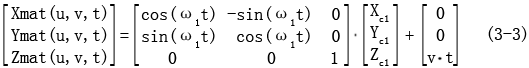求出共轭曲面各节点坐标值后,调用MATLAB绘图命令就可以显示共轭曲面的图形,并通过编制的程序,还能够以动画的形式演示两曲面作共轭运动的过程。求得的共轭曲面及两曲面作共轭运动的瞬间分别如图3-3、图3-4所示:
3.3.2 回转曲面的共轭求解
回转面是指一条曲线绕定轴回转生成的曲面。它是机械设计和加工中常见的曲面,如铣刀,砂轮,轧钢辊子等。
出于回转面在垂直于回转轴线的任何截面上所得曲线皆为圆,且圆心均在回转轴线上,若绕轴线回转的曲线无垂直于回转轴线的切线,则回转面上的任一点法线必过回转轴线。这是因为圆的切线与曲面的法线垂直,故曲线的任一点法线必在圆的法面上,即在过轴线的平面上,又绕轴线回转的曲线切线与回转轴不垂直,故任一点法线过轴线且不与轴线平行,所以必与轴线相交。
机械加工常用的盘状、指状砂轮和铣刀,以及轧钢中的圆柱轧件,都是回转面。他们的运动一般分为两种,一种是已知曲面绕某一轴线作相对回转运动(如圆柱轧件相对于轧钢辊子的运动可以认为是单纯的回转运动),其包络面是回转面;一种是已知曲面绕某一轴线作相对螺旋运动(如铣刀相对于加工工件的运动),其包络面是螺旋面。而回转面和螺旋面,都可以由某一母曲线经过相应的回转或螺旋运动得到。
根据以上分析,求已知回转面的包络面的过程可以分解为两个步骤:首先,求出任一瞬时已知曲面与所求共轭曲面的瞬时接触线;然后,把接触线作为母曲线按未知曲面的运动方程运动,这样就可以得到已知曲面的包络面,即它的共轭曲面。
基于以上回转面共轭求解的基本思路和本文提出的数字化共轭曲面求解原理与编程方法,作者开发出了数字化共轭曲面求解的专用软件,它不仅能够实现解析和数字化的回转曲面的共轭求解,能够适应多种曲面,而且求解过程简单而迅速。共轭曲面求解中繁杂的公式推导和大量的计算,都出软件在后台实现。
3.3.2.1 轧辊曲面的数字化求解
(1)轧件与轧辊的共轭运动
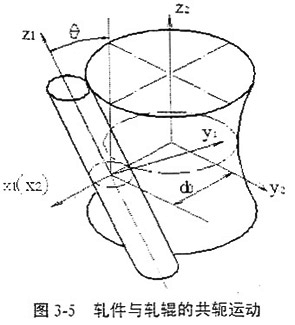
如图3-5,轧辊轴线z2竖直放置,轧件轴线为z1,两者交错成θ角度,垂直距离为d0,轧件半径为r0。在轧制过程中轧辊是转动的,现在假设轧辊不转,根据相对运动原理,则轧件就以轧辊轴线为轴作旋转运动,若轧件同时绕自身轴线回转,则轧件的相对运动包括自转和公转。以轧件为已知曲面Σ1,它与坐标系S1固连,转动角速度为ω1,Σ1上的各点在S1中的用规则矩阵表示为X1(1),Y1(1),Z1(1);以轧辊为所求的共轭曲面Σ2,它与坐标系S2固连,转动角速度为ω2,则轧件的运动可以用矩阵变换的形式表示为:
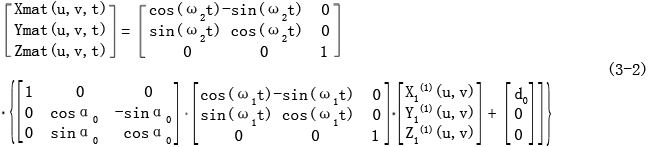
式中,三维数组Xmat(u,v,t),Ymat(u,v,t),Zmat(u,v,t)表示轧件曲面在轧辊坐标系S2中运动形成的曲面族。利用数字化共轭曲面的求解步骤,即可完成轧辊曲面的求解。为使求解简化,可充分利用回转曲面的特殊性,即绕自身转动后的回转曲面还是原回转曲面;无论对于共轭曲面的相对运动是转动还是螺旋运动,两曲面接触线的形状是不变的。那么,我们可以取t值为一个合适的范围,得到两曲面完整的接触线,然后使接触线按照与两曲面相对运动相同的运动过程运动,得到的曲线族就是所求的共轭曲面。这样,既减少了计算量,同时又避免了出现“一对多”映射时将t分段造成的各个共轭曲面片衔接困难的问题。
求出接触线后,使接触线按照两曲面运动关系运动,所得到的曲线族就是所求的共轭曲面,也即轧辊曲面。
(2)轧辊面的数字化共轭求解
本文用VC++和MATLAB开发了一套共轭曲面求解软件Conjugater1.0,它能够进行轧钢辊子曲面、铣刀加工面、直齿面以及鼓形齿面等的自动求解和辅助设计。
应用软件Conjugater1.0求解轧辊曲面:已知轧件曲面是圆柱面,输入表达式或各节点坐标值后,可以显示其曲面形状如图3-6所示;根据各节点值以及输入的运动和相对位置参数,进行共轭曲面求解运算,可以得到与已知曲面共轭的两个曲面如图3-7所示,这两个曲面都满足共轭条件的;根据实际需要,取与已知曲面外共轭的共轭曲面(如图3-8),这就是满足条件的轧辊曲面。


3.3.2.2 铣刀加工面的数字化求解
(1)铣刀与其加工面的共轭运动
与轧辊的求解相似,对于回转型刀具,也可以先求出两共轭曲面的接触线,然后使接触线按照两曲面特定的运动关系运动,就得到要加工的曲面。刀具加工的曲面可以是回转面,也可以是螺旋面。铣刀及其加工面如图3-9所示。
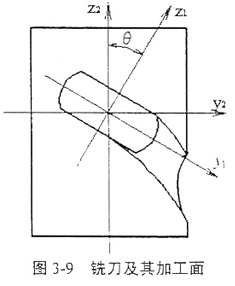
设已知接触线为C1,它可以由三个一维数组Xc1,Yc1,Zc1表示,螺旋运动的角速度为ω,轴向移动速度为v,则由它生成的螺旋面可以用如下的坐标变换表示为:
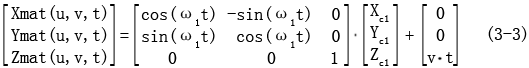
(2)铣刀加工面的数字化求解
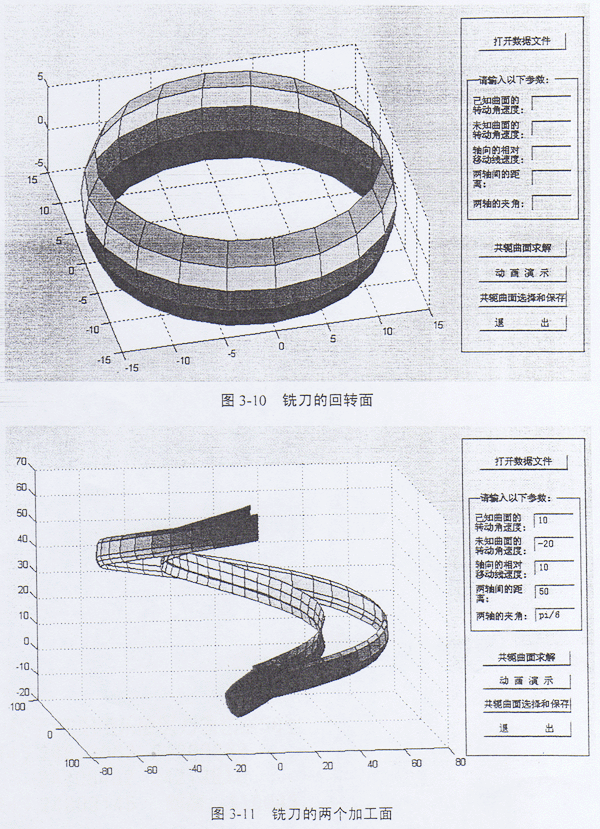
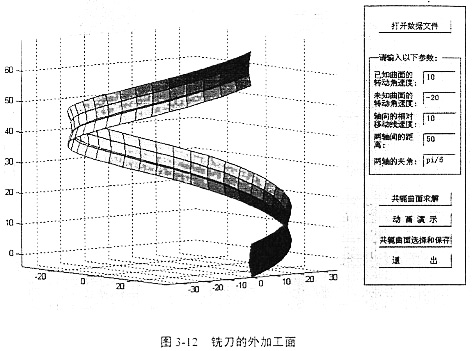
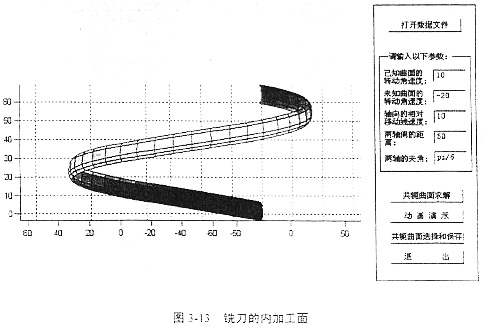
借助于软件Conjugater1.0求铣刀加工的过程与求解轧辊曲面的过程相同。输入输出界面和结果如图3-10、图3-11、图3-12、图3-13所示。最后得到如图的两个螺旋面,这两个螺旋面都是满足共轭条件的,图3-12表示铣刀在工件实体的外圆加工所得的曲面,图3-13表示铣刀在工件的内壁加工所得的曲面。应用时可根据实际情况选取。
3.4 小结
(1)本章充分利用MATLAB的计算特点来处理数字化共轭曲面的求解及仿真,用一维数组、二维数组、三维数组分别与点的运动轨迹、曲面、曲面族相对应;用坐标分解的方法使MATLAB可以方便地处理三维曲面;
(2)提出了在三维数组中抽取出所需的一维数组的概念,使数据处理形象直观;
(3)在计算过程中用一个简单的函数实现了优化的功能,大大降低了计算复杂程度;并且优化所得的结果是点(uj,vk)在整个轨迹插值曲线中使ψ(uj,vk,t)=0的点,而不是在有限个已知的轨迹离散数据点中使ψ(uj,vk,t)为最小值的点,这样就突破了有限个数据点的限制,最大限度地利用了已知信息,使计算结果更精确。
(4)本章利用自行开发的数字化共轭求解软件,分别对任意数字曲面和回转曲面问题进行了数字化共轭求解计算,得到了满意的计算结果,验证了理论、模型算法和软件的正确与可用性。
上一页
下一页