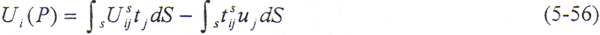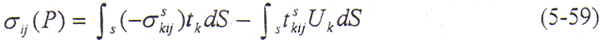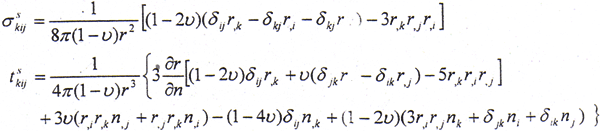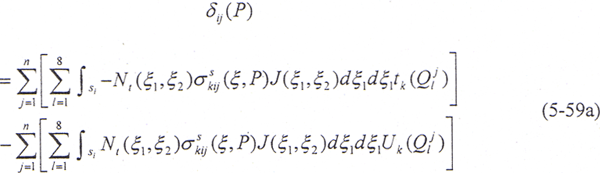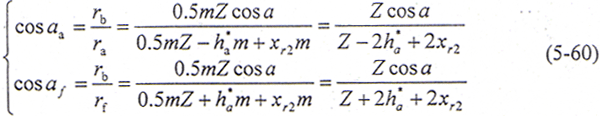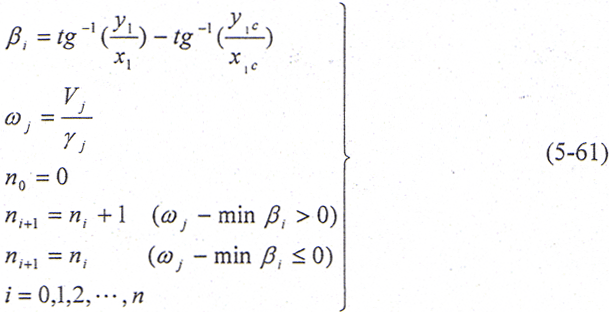5.3.2.2 鼓形齿联轴器传动的轴系固有频率
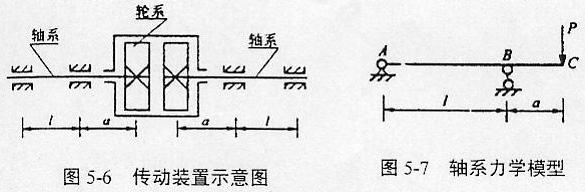
共轭鼓形齿联轴器传动装置示意图如图5-6所示,其相应的轴系力学模型如图5-7所示,模型中自由端载荷P=G/2,G为联轴器的重量。
在静态下,由P所产生的静挠度为
y0=-[Pa2(l+a)]/(3EI) (5-32)
即
p=3EIy0/[a2(l+a)]=ky0 (5-33)
式中,E为轴材料的弹性模量,I为轴的轴惯性矩,对于圆轴I=πD4/64,D为圆轴直径;k为轴的静刚度系数。
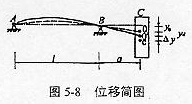
在动态情况下,设轴以转速n转动,其角速度为ω=nπ/30。由于渐开线内齿轮和鼓形外齿轮间有径向位移△y,因此,质心C和转动中心不重合,轴系在转动过程中则产生离心力F,由此将发生动挠度yd,其位移简图如图5-8所示。
轴系在转动过程中产生的离心力大小为
F=mRω2=m(△y+yd)ω2 (5-34)
式中,m=P/g。
因为轴在其材料弹性范围内工作,所以有
F=kyd=m(△y+yd)ω2 (5-35)
即
yd=mω2△y/(k-mω2)=△y/(k/mω2-1) (5-35a)
由式(5-35a)可知,令k/(mω2)-1=0,得到轴系的固有频率为
ω0=(k/m)1/2=(g/y0)1/2 (5-36)
5.3.2.3 计算实例
一共轭鼓形齿联轴器台架试验装置,渐开线内齿轮和鼓形外齿轮间径向位移△y=0.7mm,联轴器的重量G=150N,两支座间的轴间距离l=1500mm,联轴器到支座间的距离a=150mm,轴的当量直径D=50mm,确定该联轴器轴系固有频率ω0及临界转速n0。
(1)轴系的固有频率 根据式(5-36)及已知数据,可得
ω0=261rad/s
(2)临界转速
n0=60ω0/2π=2494r/min
通过对共轭鼓形齿联轴器传动系统的轮系和轴系分别进行定性和定量分析,对其在传动过程中的振动机理和系统的固有频率有了更深的了解,并提出共轭鼓形齿联轴器传动的振动诱因主要来源于轴系的观点。事实上,鼓形齿联轴器传动系统的振动机理与固有频率受轮系与轴系的共同影响,但由于轮系刚度比轴系的弯曲刚度大得多,故轮系的固有频率远远超出轴系的固有频率,所以鼓形齿联轴器在重载低速下工作时将远离轮系固有频率,因此,轮系的固有频率对传动系统的性能和设计不会造成直接影响,而轴系的固有频率则是传动系统设计、减振与防御共振的主要依据。
对共轭鼓形齿联轴器传动装置,应避免在其轴系固有频率附近工作,否则,将发生共振,从而,致使传动系统噪音极剧增加,振幅迅速加大,若不采取措施,最终会导致传动系统破坏。
共轭鼓形齿联轴器传动减振与共振防御的措施较多,常用的方法是改变齿轮传动系统的固有频率,如改变传动系统轮系转动质量和转动惯量,改变传动系统轴系的刚度,此外,也可以在传动系统中采用被动的隔振、消振和降振措施。总之,共轭鼓形齿联轴器传动的振动问题研究是一项具有理论和实际价值的工作,它的深入研究不仅有利于这种新型传动件的优化设计,对加工、制造技术和安装使用都将起到重要指导作用。
5.3.3 鼓形齿联轴器传动的强度分析
5.3.3.1 接触强度分析
在研究齿轮传动的接触应力和形变时,到目前为止,传统的方法就是利用线接触的平行圆柱体代替某一具体啮合位置的实际齿面,把该啮合位置的齿廓曲率半径当做圆柱体的半径。这种替换近似计算方法虽然有许多与实际情况不符之处,但迄今为止,在齿轮传动的强度设计中仍采用这一方法计算接触问题,即所谓赫兹公式。赫兹公式的应用主要受到以下条件的限制:
(1)两物体为均匀各向同性的弹性体;
(2)两物体接触面与物体表面相比是极微小的;
(3)作用力与接触面垂直;
(4)加载后材料中的应力不超过其比例极限;
(5)圆柱体为无限长。
这些限制条件对渐开线直齿圆柱齿轮传动是基本适用的,然而,对鼓形齿联轴器传动则存在较大差异,即使是共轭鼓形齿联轴器传动的线接触问题,传动的不同轴性等因素,使得该传动的接触状态与直齿圆柱齿轮传动相差甚远。因此,鼓形齿联轴器传动的接触强度问题不能简单套用赫兹公式。通常采用数值计算方法进行计算[93-102],比较常用的数值计算方法是有限元法和边界元法。
(1)接触问题有限元法
对于共轭鼓形齿轮传动的接触问题,除了应满足弹性力学的一般控制方程外,在接触面上还应满足接触面力和接触面位移边界条件,即满足力学平衡条件,法线方向上满足位移非嵌入条件,且不计摩擦。在接触有限元法的求解计算中,为了准确描述接触面各接触点对的状态,将其接触状态分别定义为连续状态、滑动状态和分离状态,这样可以定出不同状态下的边界条件关系式。将接触点对不同接触状态下的边界条件关系式用适当的系数矩阵表示,接触有限元矩阵形式的方程为
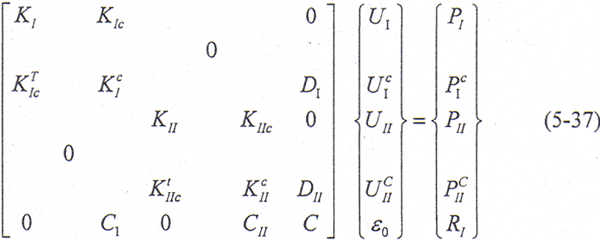
式中,
K、U、P、R——刚度矩阵、位移向量、载荷和接触面力向量;
角标Ⅰ、Ⅱ——相应两个接触的相互共轭的鼓形外齿轮和直齿内齿轮;
角标C——对应的接触区域;
CⅠ、CⅡ——相应齿轮的接触点对位移协调条件的系数矩阵;
角标T——对应的非接触区域;
ε0——位移常数矩阵;
DⅠ、DⅡ、D——接触点对力学平衡条件的系数矩阵。
若用三角分解算法进行分解消元运算,使与接触面有关的刚度矩阵变换成为单位矩阵,同时求出相应的系数矩阵的改变DⅠ、DⅡ和载荷向量的改变PⅠ′、PⅠC、PⅡ′、PⅡC,则矩阵方程成为
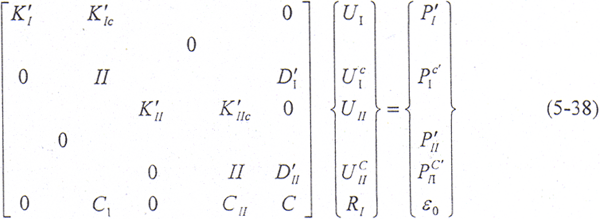
式中,Ⅱ为单位矩阵。
由此可求出如下接触面柔度方程
F{Rl}=-{SP}-{ε0} (5-39)
式中,F——接触面柔度矩阵;
SP——载荷的接触点对上产生的相对位移向量。
把接触有限元刚度方程凝缩为仅与接触面力有关的柔度方程,使得接触问题的迭代运算规模大大降低,且求解效率提高,能较方便地对共轭鼓形齿轮传动这类三维复杂啮合传动进行数值计算分析。
(2)接触问题边界元法
接触边界元是将接触域内任意点的位移与应力值用边界值即边界单元的面力与位移来表示。其边界元法的基本方程为
Uli=∫ΓPkUiK*dΓ+∫∫ΩbkUlK*Plk*dΓ (5-40)
式中,Uli——在i点第l个方向上的位移;
UlK*、PlK*——基本解。
将(5-40)式离散并用矩阵表示,则可得共轭鼓形齿轮传动的接触边界元方程
HU=GT (5-41)
式中,H、G——3n×3n阶的系数矩阵;
U、T——边界节点的位移分量和接触面力分量。
将(5-41)式中的未知量移到等式左边,以x表示,将已知量移到等号右边,以F表示,系数矩阵以A表示,则可得显式形式的方程
Ax=F (5-42)
用高斯消去法求解线性方程组(5-42),便可求得所有边界未知位移分量U和接触面力分量T。
(3)接触有限元与边界元计算模型
对共轭鼓形齿轮的有限元网格划分,采用平行加密法划分,形成接触分析粗网格,然后对接触区作局部细分,求出接触点对坐标。
对共轭鼓形齿轮用边界元法进行接触问题的研究与分析时,首先只需对边界即齿廓表面进行单元划分,然后对每个啮合点即接触区进行局部细分,不需像有限元法那样,需从表到里将整个齿轮轮齿进行划分。
(4)计算实例
基于上述接触问题的有限元与边界元计算模型和前面的载荷分析,对一模数m=5mm、齿数Z=40、分度圆压力角a=20°、分度圆直径d=200mm、齿宽b=20mm、齿轮材料的弹性常数E=2.1×105N/mm2、泊松比μ=0.3、传递扭矩Mn=300N·m的共轭鼓形齿联轴器鼓形齿轮Ⅰ进行了接触应力计算,其简图如图5-9所示。该问题接触应力的有限元与边界元数值解和接触应力分布曲线分别如表5-1、图5-10所示。曲线①(虚线)为接触应力的有限元解;曲线②(实线)为接触应力的边界元解。
表5-1 接触应力的有限元边界元数值解
| 齿高/mm |
0 |
2 |
4 |
6 |
8 |
10 |
| 有限元解/(N/mm2) |
-1150 |
-970 |
-840 |
-650 |
-500 |
-320 |
| 边界元解/(N/mm2) |
-1000 |
-925 |
-800 |
-650 |
-520 |
-370 |
由表5-1与图5-10可得如下结论:
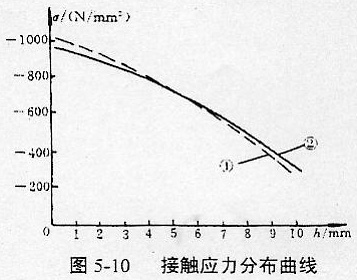
(1)接触应力的两种数值解相当接近,只是在开始进入啮合和脱离啮合时有些差异。这主要是算法和计算模型差异所致,但接触应力的变化趋势是一致的,且齿高中部附近接触应力的两种解答完全一致。
(2)由于两种解答的一致性,在研究轮齿齿廓接触应力时,易选用边界元法,这样,可减少前处理工作量,提高计算效率。
(3)轮齿在啮合传动接触过程中,齿根处接触应力与弯曲应力同时达到最大值。其原因主要是齿根部的刚度大于齿顶部,齿顶部的变形以弹性弯曲变形为主,齿根部则以接触变形为主。
5.3.3.2 弯曲强度分析
鼓形齿联轴器在传递载荷的过程中,其传动齿轮的轮齿处于悬臂受弯工作状态。为了保证联轴器传动齿轮在工作时不致发生断齿现象,齿根的最大危险应力必须低于极限值,为此,必须对鼓形齿联轴器传动进行弯曲强度计算。通常在一般齿轮弯曲强度设计计算中采用简单平载面计算法和折载面计算法,这两种方法的优点是简单直观,易于操作,能基本满足设计要求;其不足就是这两种方法都是把轮齿简化为一个悬臂梁的力学模型,应用材料力学的理论来求解,显然,这里存在误差。因为材料力学关于梁的理论,只适用于载荷作用点与支点的距离比梁的横载面高度大得多的梁,亦即所谓浅梁的情况。但此处的轮齿受载力学模型则不满足这种条件,它实际上是一个短而宽的悬臂梁,应属于深梁的范围[103-110]。深梁的弯曲问题材料力学已无能为力,须用弹性力学理论求得解析解,例如可用复变函数解法,通过求解半无限大板边界有齿形突起的模型录求应力解。但这种方法在工程设计中往往不够现实,所以又出现了一种短宽悬臂梁的所谓半经验解法,这种方法是纯材料力学解法和弹性力学解法的一种折中方法,虽然从数学和力学的观点来看不够严密,但是与试验结果比较相符,因此,这种方法在很多齿轮传动的弯曲强度分析和计算中受到广泛采用[111-119]。对于鼓形齿联轴器传动的弯曲强度计算本文采用边界元数值算法。
(1)弯曲强度的三维边界元方法
边界元法是从积分方程方法发展而来的,是继有限差分法和有限元法之后的一种新的有效的数值分析方法。本节按照边界积分方程直接法,从三维弹性问题基本微分方程和相应的边界条件出发,建立该三维问题的边界积分方程,然后采用离散插值方案数值处理技术,化边界积分方程为边界元方程,最后在微机上对鼓形齿联轴器啮合时的弹性变形进行三维边界元计算分析。
(2)三维弹性问题的边界积分方程
对于三维弹性问题,若以位移为其本未知量,则其基本微分方程和边界条件可表示为
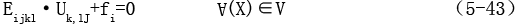
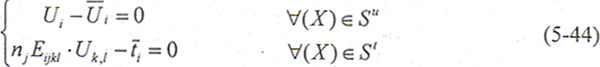
式中,Uk——某一方向位移矢量;
Uk,l——位移Uk对l方向求一阶偏导;
Uk,lj——位移Uk对l和j求二阶偏导;
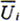 ——给定位移边界SU上位移Ui的已知量;
——给定位移边界SU上位移Ui的已知量;
nj——表面单位法矢分量;
Eijkl——弹性系数张量;
fi——体积力分量;
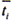 ——给定面力边界St上面力ti的已知量。
——给定面力边界St上面力ti的已知量。
V——三维域;
X——三维域中任意点的坐标列向量。
对于各向同性弹性体,根据物理关系可得弹性方程为
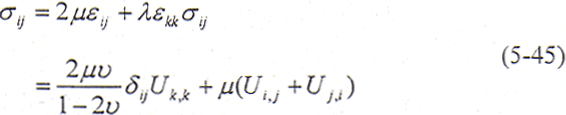
式中,σij——正应力;
δij——克罗内克定义符,且有
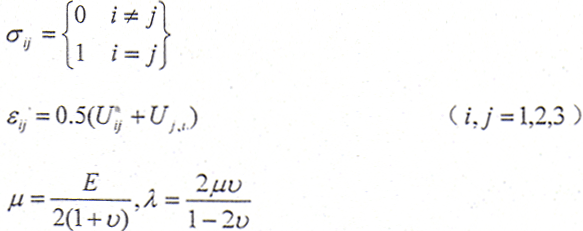
由此,基本方程和边界条件(5-43)、(5-44)式可写为
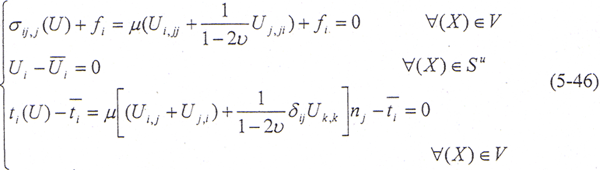
对于以上三维弹性问题的边值问题,采用加权余量法可导出域内位移的积分方程为

式中,
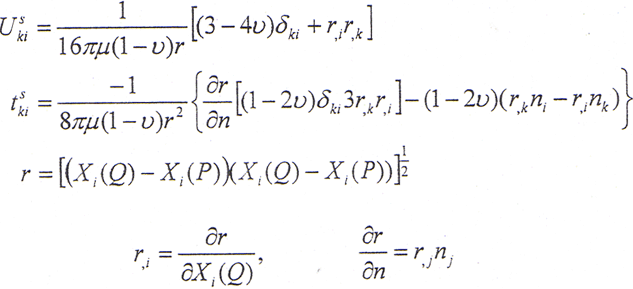
式(5-47)是区域内任意点的位移分量Uk(P)和边界上的表面力分量ti、位移分量Ui之间的关系,其中Uski和tski分别为线弹性静力问题的基本解和与基本解对应的表面力。然而,我们所感兴趣的则是边界上的位移分量和表面力之间的关系。Q为域内点,当源点P出域内趋于边界点时,可导出边界积分方程为
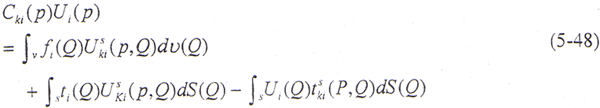
式中,Cki(P)是与P点处表面几何特征有关的系数,一般地
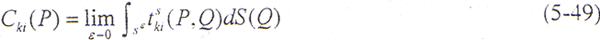
对于三维光滑边界,系数Cki(P)为三阶方阵,即

(3)三维弹性问题边界积分方程的数值解法
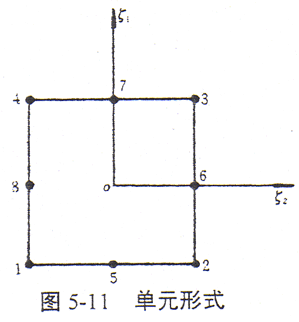
一般情况下,不可能应用解析方法来解积分方程,而必须采用近似的数值解法。这里采用边界元方法,边界元法将区域的边界分割n个边界单元,整个边界上的积分以n个边界单元上的积分和表示,在本文中采用4~8节点的变节点等参元,当只有四个角点时,即为线性元,有8个节点时为二次等参元。对于疏密过渡区可采用变节点单元,以适应各种复杂结构的需要,单元形式如图5-11所示。
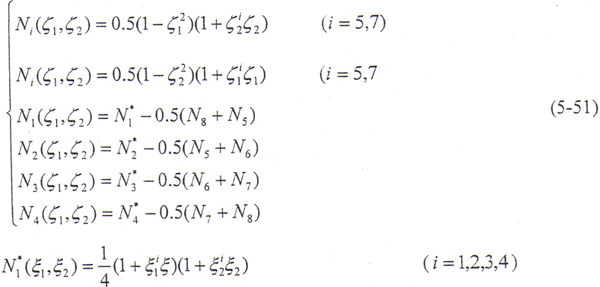
式中,ζia——单元的第i个节点的第a(a=1,2)个局部坐标分量。单元内任一点的整体坐标、位移和面力可分别表示为
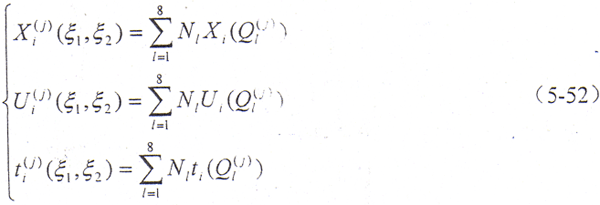
此处假定将整个边界离散划分为N个单元,将(5-52)式代入边界积分方程(5-48)式,在不考虑体力情况下,可得离散后的边界积分方程为
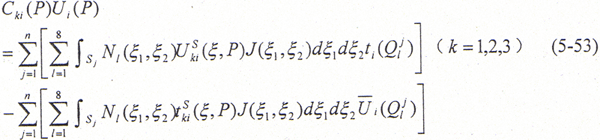
在上述n个边界单元中,若将n1个单元的表面力分量和(n-n1)个单元的位移分量作为边界条件给出,那么(5-53)式可进一步改写成
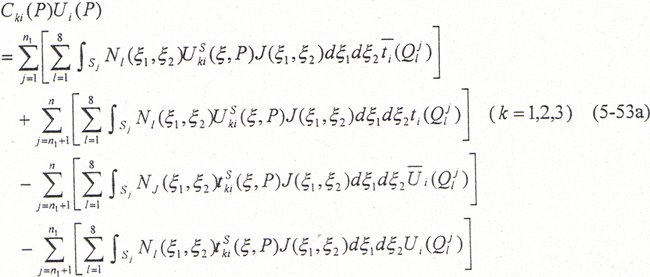
对于边界上每一个节点均可建立三个线性代数方程,那么,对于n个节点,就可以形成一线性代数方程组,可以用以下形式表示:
HU=GT (5-54)
式中,H、G——3n×3n阶的系数矩阵,其元素Hij为3×3阶矩阵;
U、T——边界单元节点的位移分量和表面力分量。
式(5-54)可写为
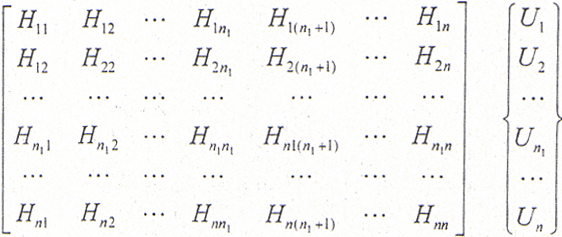

将(5-54)式中未知边界量U、T及相应的系数归并到方程左边,已知量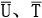 及相应的系数归并到方程右边,即可得到如下形式的方程:
及相应的系数归并到方程右边,即可得到如下形式的方程:
Ax=F (5-55)
用高斯消去法求解线性方程组(5-55)式,便可求得所有边界未知的位移分量U和表面力分量T。
在求出边界节点的面力及位移后,由(5-47)式可求出域内任一点i处的位移为
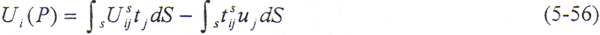
其几何方程为
εij=(Ui,j+Uj,i)/2 (5-57)
物理方程为

将式(5-56)式代入(5-57)式,然后代入(5-58)式,即可得到区域内应力分量的表达式为
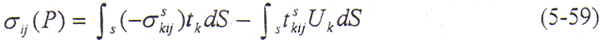
式中,
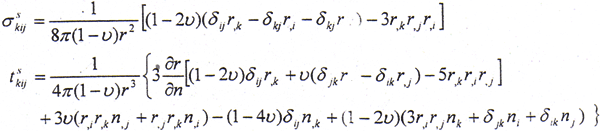
由于边界面式离散化的,(5-59)式可写成离散形式
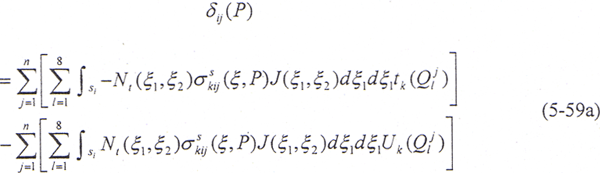
至于边界点的应力计算,可以利用已经求得的边界单元的节点位移和面力,求出边界单元内任一点的应力。
(4)弯曲强度的三维边界元计算
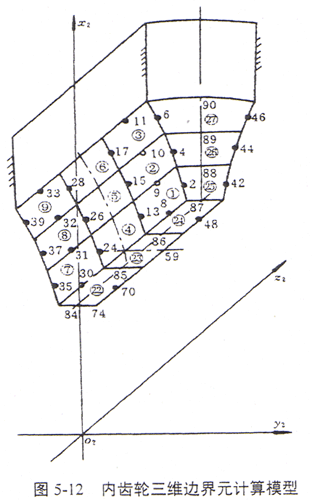
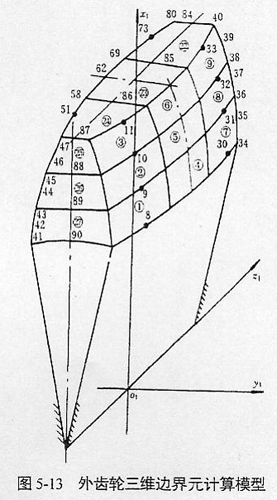
基于上述分析,可采用三维边界元法对鼓形齿联轴器传动的弯曲应力与形变等进行数值计算与分析,其内外齿轮的三维边界元计算模型分别如图5-12、图5-13所示。
5.4 共轭鼓形齿联轴器传动多齿啮合分析
鼓形齿联轴器内外齿轮在传动过程中,受载之前,即不考虑弹性弯形的情况下,各齿对间的啮合状态可通过各齿对间工作侧的最小间隙角βi进行模拟;而受载后各啮合齿对将分别产生弹性变形,为了补偿轮齿变形后齿廓间可能产生的间隙,使内外齿轮仍然保持连续传动,以继续传递载荷,主动轮轮体必然产生一个顺其自身转动方向的变形角ω。当载荷增大时,各啮合受载齿对的弹性变形也随之增大,则变形角ω也必然随之增加,因此,外载荷与鼓形齿联轴器主动齿轮的变形角成正比,即变形角的大小反映了外载荷的大小。当传递的载荷增大到使变形角大到一定程度时,就可以消除与理论啮合齿对相邻的非理论啮合齿对齿廓间的最小间隙,从而,使该非理论啮合齿对也承受部分传动载荷而产生相应的弹性变形。当外载荷继续增加,使变形角大到又可消除另外的非理论接触齿对齿廓间最小间隙,使该齿对也参与啮合,如此下去,就产生了理论接触和非理论接触的鼓形齿联轴器的多齿啮合问题。
5.4.1 理论啮合接触线分析
由(5-10)式和(5-12)式,通过计算,可以得到内外齿轮啮合齿面上接触线坐标,由计算出的坐标值即可绘出接触线图形。计算式中对ψ的要求是:
ψf≤ψ≤ψa
式中,ψa=tanaa,ψf=tanaf;aa、af——内齿轮齿顶和齿根压力角。且
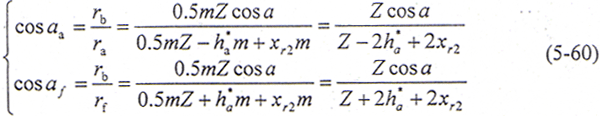
以m=3mm,Z=56,θ=1.5°,xr1=xr2=0,ha*=1,齿宽按需要取到足够大为例计算,确定-90°≤φ≤270°区间的若干条接触线。由建立的齿面方程可知,φ=0时,齿面处于纯翻转位置。由(5-60)式计算得aa=12.968°,af=24.866°。
通过计算,得到内外齿轮齿面接触线坐标,表5-2给出部分坐标值计算结果。图5-16所示的为φ间隔2.5°时,内外齿轮齿面转过一圈所形成的齿面接触线。
表5-2 外齿轮齿面接触线坐标
(m=3mm Z=56 a=20° θ=1.5° xr1=xr2=0 ha*=1)
| φ/(°) |
a1/(°) |
z1/mm |
x1/mm |
φ/(°) |
a1/(°) |
z1/mm |
x1/mm |
| -10.0 |
12.968
15.785
18.526
21.181
23.745 |
80.313
15.406
8.358
5.666
4.252 |
81.305
82.046
83.246
84.653
86.241 |
170.0 |
12.968
15.785
18.526
21.181
23.745 |
-80.313
-15.406
-8.358
-5.666
-4.252 |
81.305
82.046
83.246
84.653
86.241 |
| 10.0 |
12.968
15.785
18.526
21.181
23.745 |
3.204
2.863
2.607
2.412
2.263 |
80.924
81.963
83.196
84.616
86.212 |
190.0 |
12.968
15.785
18.526
21.181
23.745 |
-3.204
-2.863
-2.607
-2.412
-2.263 |
80.924
81.963
83.196
84.616
86.212 |
| 30.0 |
12.968
15.785
18.526
21.181
23.745 |
2.571
2.501
2.449
2.413
2.392 |
80.911
81.949
83.182
84.602
86.197 |
210.0 |
12.968
15.785
18.526
21.181
23.745 |
-2.571
-2.501
-2.449
-2.413
-2.392 |
80.911
81.949
83.182
84.602
86.197 |
| 50.0 |
12.968
15.785
18.526
21.181
23.745 |
2.754
2.746
2.749
2.762
2.785 |
80.899
81.936
83.169
84.588
86.182 |
230.0 |
12.968
15.785
18.526
21.181
23.745 |
-2.754
-2.746
-2.749
-2.762
2.785 |
80.899
81.936
83.169
84.588
86.182 |
| 70.0 |
12.968
15.785
18.526
21.181
23.745 |
3.009
3.029
3.058
3.096
3.142 |
80.888
81.925
83.157
84.576
86.170 |
250.0 |
12.968
15.785
18.526
21.181
23.745 |
-3.009
-3.029
-3.058
-3.096
-3.142 |
80.888
81.925
83.157
84.576
86.170 |
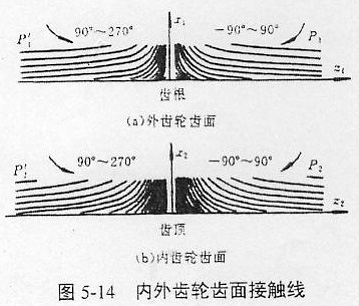
由图5-15所示可知,φ在-90°~90°范围变化时,从-90°到小于0°的某一角度范围,内外齿轮齿面无接触线,此后,接触线在内外齿轮齿面中截面的右外侧从外齿轮齿顶P1和内齿轮齿根P2进入,逐渐向齿宽中截面位置移动,在小于90°的某一角度结束,接触线弯曲方向及倾斜方向如图5-14所示。开始进入接触和最后脱离接触的φ值由齿轮参数决定,φ在90°~270°范围变化时,接触线在内外齿轮齿面中截面的左外侧P2′、P1′啮入,转角位置与右外侧啮合对称。内外齿轮齿面左右两则的接触线分别呈以x1、x2坐标轴为对称的形状。
5.4.2 多齿啮合分析
5.4.2.1 多齿啮合数学模型
根据以上分析,可建立鼓形齿联轴器多齿啮合问题数学模型如下:
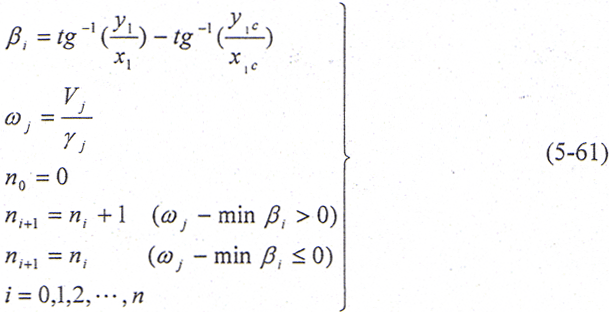
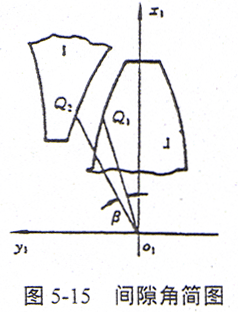
式中,βi为第i对齿间对应于齿面Ⅰ上点Q1(x1,y1,z1)处的间隙角(如图5-15所示);minβi为第i对齿间的最小间隙角;x1,y1,z1为与外齿轮Ⅰ固连的动座标系S1下的座标;x1c,y1c,z1c为与齿面Ⅰ上一点Q1相对应的齿面Ⅱ上的点Q2的座标在座标系S1下的变换座标;ωj为受载最大齿对的简化集中载荷作用点处的切向弹性变形量,含内外齿两部分;γj为j点所在处的向径大小;ni为同时接触齿对数。
5.4.2.2 实际啮合齿对计算
本节第一部分在不考虑弹性变形的前提下,基于齿轮传动几何关系刚性啮合原理之上的理论啮合对数,在几何参数为表5-3所示情况下,当鼓形齿联轴器在转过360°/Z角度的过程中,经进一步分析,其一啮合区的理论接触齿对在4对与5对之间变化,即整个联轴器在传动过程中,理论接触齿对则在8对与10对间变动。将某齿对定义为1号齿对,且以该齿对理论上刚开始啮合作为初始状态开始转动,在鼓形齿联轴器转过7°时,第5号齿对脱离啮合,当继续转动至360°/Z角度时,0号齿对开始进入啮合,这样便完成一个周期。
表5-3 鼓形齿联轴器几何参数
| 参数 |
内齿数 |
鼓形外齿轮 |
| 模数m |
3(mm) |
3(mm) |
| 齿数Z |
40 |
40 |
| 分度圆压力角α |
20° |
20° |
| 分度圆直径d |
120(mm) |
120(mm) |
| 齿顶圆直径da |
115.2(mm) |
124.8(mm) |
| 齿根圆直径df |
124.8(mm) |
113.7(mm) |
| 齿宽b |
30mm |
20mm |
| 工作倾角θ |
3° |
在实际受载轮齿变形后,其接触齿对将发生变化。应用三维弹性边界元法求出鼓形齿联轴器在实际工作受载后,其受载最大轮齿工作齿面上各啮合点的弹性变形量以及相应的变形角,从中并求得简化载荷作用处的变形角ωj,其值分别为内、外轮齿载荷作用处的变形角之代数和,即
ωj=ωjⅠ+ωjⅡ (5-62)
其中,外齿轮弹性变形的三维边界元解答如表5-4所示(内齿轮从略)。
表5-4 外齿轮弹性变形的三维边界元解答(部分)
| 节点 |
弹性变形量(mm) |
变形角(°) |
| NO |
U |
V |
W |
ωj |
| 1 |
0.000000000 |
0.000000000 |
0.000000000 |
0.000000000 |
| 2 |
-0.000175380 |
-0.000431121 |
0.000049957 |
0.000426817 |
| 3 |
-0.000374515 |
0.001251580 |
-0.000081436 |
0.001216990 |
| 4 |
-0.000614887 |
-0.003520113 |
-0.000147521 |
0.003363150 |
| 5 |
-0.000281512 |
-0.003161834 |
-0.000107730 |
0.002981080 |
| 6 |
-0.000094073 |
-0.002939400 |
0.000062302 |
0.002735390 |
| 7 |
0.000119509 |
-0.002584201 |
0.000089001 |
0.002374020 |
| 8 |
0.000000000 |
0.000000000 |
0.000000000 |
0.000000000 |
| 9 |
-0.000358453 |
-0.001366520 |
-0.000090823 |
0.001328820 |
| 10 |
-0.000295010 |
-0.003325547 |
-0.000120167 |
0.003135420 |
| 11 |
0.000116598 |
-0.002417326 |
0.000087937 |
0.002206900 |
| 12 |
0.000000000 |
0.000000000 |
0.000000000 |
0.000000000 |
| 13 |
-0.000200144 |
-0.000447580 |
0.000038178 |
0.000443054 |
| 14 |
-0.000394231 |
-0.001515470 |
-0.000079434 |
0.001473620 |
| 15 |
-0.000714289 |
-0.003701127 |
-0.00114053 |
0.003536080 |
| 16 |
-0.000312970 |
-0.003470020 |
-0.000114053 |
0.003271660 |
| 17 |
0.000110460 |
-0.003095265 |
-0.000010400 |
0.002880380 |
表5-4中节点编号详见5.3节中边界元计算模型。
由此,根据多齿接触问题的数学模型(5-61)即可求得鼓形齿联轴器在转360°/Z角度的过程中,各瞬时的实际接触齿对情况,其实际接触齿对状态列表5-5所示
表5-5 实际接触齿对状态表
| 转角φ |
齿对号 |
| 7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
-1 |
| 实际接触状态 |
| 48.53 |
|
+ |
0 |
0 |
0 |
0 |
0 |
+ |
|
| 49.53 |
|
+ |
0 |
0 |
0 |
0 |
0 |
+ |
|
| 50.53 |
|
+ |
0 |
0 |
0 |
0 |
0 |
+ |
|
| 51.53 |
|
+ |
0 |
0 |
0 |
0 |
0 |
+ |
|
| 52.53 |
|
|
0 |
0 |
0 |
0 |
0 |
+ |
|
| 53.53 |
|
|
0 |
0 |
0 |
0 |
0 |
+ |
+ |
| 54.53 |
|
|
0 |
0 |
0 |
0 |
0 |
+ |
+ |
| 55.53 |
|
|
+ |
0 |
0 |
0 |
0 |
+ |
+ |
| 56.53 |
|
|
+ |
0 |
0 |
0 |
0 |
+ |
+ |
| 57.53 |
|
|
+ |
0 |
0 |
0 |
0 |
0 |
+ |
注:“0”——表示理论接触齿对;“+”——表示由变形出现的接触齿对。
5.5 小结
本章根据共轭曲面理论和啮合原理,创立了共轭鼓形齿联轴器传动理论和研究策略,主要取得了以下成果:
(1)推出了鼓形齿联轴器轮齿接触线及鼓形齿面方程;为后面的啮合特性分析奠定了基础;
(2)对鼓形齿联轴器传动的静力学、动力学、接触强度和弯曲强度等力学特性进行了全面研究。在静力学分析中,提出了在弹性状态下,齿面载荷均匀分布和齿间载荷按各啮合齿对瞬时综合刚度正比分配的载荷分配模型,解决了在鼓形齿联轴器设计、可靠性研究和多齿啮合分析中的计算载荷问题。在动力学分析中,提出了将鼓形齿联轴器传动这一弹性动力学系统离散化的思想,并求解证实了共轭鼓形联轴器传动的振动诱因主要来源于轴系的观点,为共轭鼓形齿联轴器传动的减振与防御提供了理论依据。在强度分析中,对其接触与弯曲强度分别采用不同的数值方法进行了对比研究,得到了一些有意义的结论,特别是数值计算模型和计算结果为多齿啮合分析提供了理论支撑;
(3)提出了理论间隙角的概念,建立了最小间隙角的优化数学模型,并由此求得了共轭鼓形齿联轴器在转过一个齿距角的过程中不同时刻的最小间隙角的分布规律和理论接触齿对数;
(4)提出了变形角的概念,构建了共轭鼓形齿联轴器多齿啮合数学模型,并应用三维弹性边界元方法,对一鼓形齿联轴器进行了计算分析,求得了实际啮合齿对数,并首次得到了该传动装置的一些有价值的结论。这些结论将对该传动装置今后的设计思想和设计标准产生较大的影响。
上一页
下一页



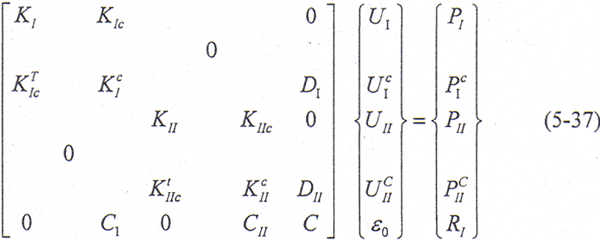
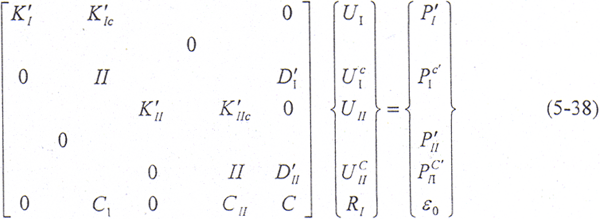


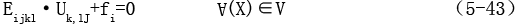
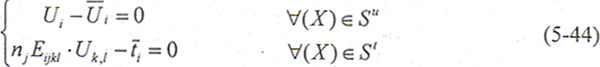
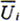 ——给定位移边界SU上位移Ui的已知量;
——给定位移边界SU上位移Ui的已知量;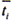 ——给定面力边界St上面力ti的已知量。
——给定面力边界St上面力ti的已知量。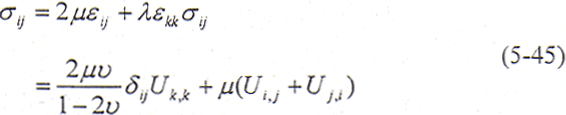
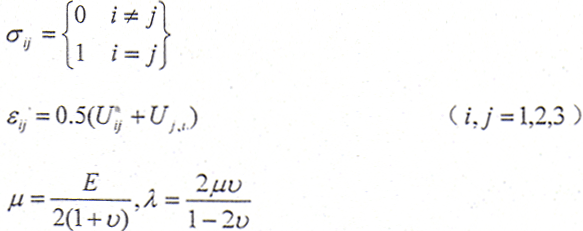
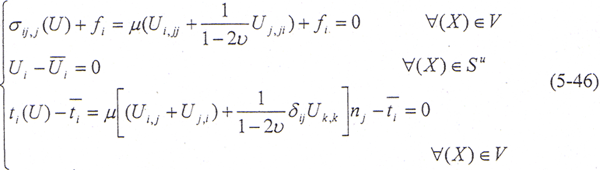

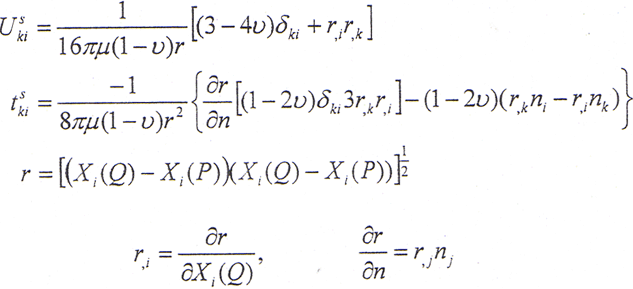
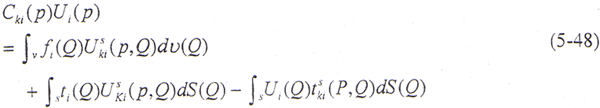
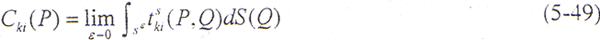


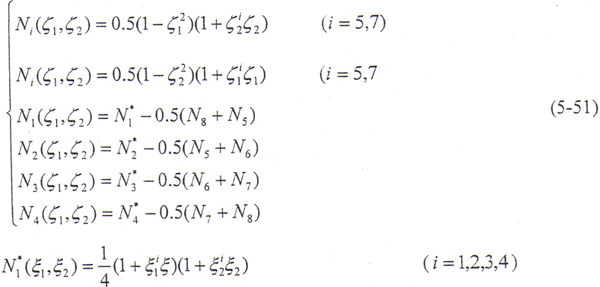
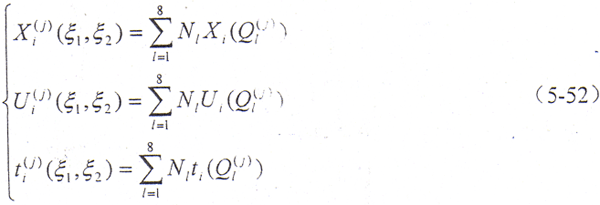
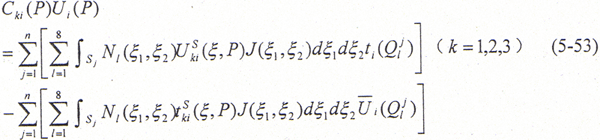
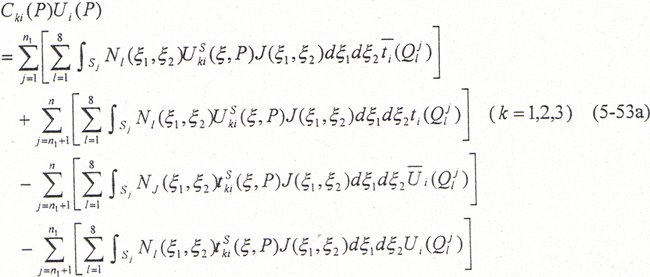
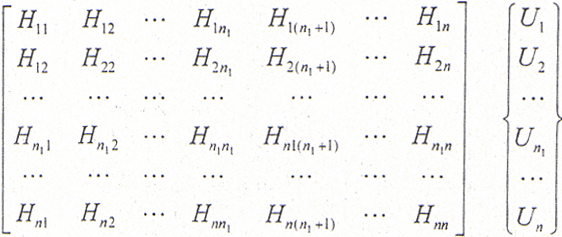

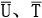 及相应的系数归并到方程右边,即可得到如下形式的方程:
及相应的系数归并到方程右边,即可得到如下形式的方程: