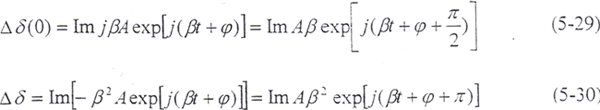5 共轭鼓形齿联轴器传动啮合特性分析
5.1 引言
前面研究了共轭曲面的数字化方法及其在数字齿面设计中的应用,为实现数字化设计与加工、特别是鼓形齿轮的数字化设计与加工一体化奠定了基础。
本章研究鼓形齿轮在一新型传动装置中的应用---共轭鼓形齿联轴器。主要讨论共轭鼓形齿联轴器鼓形齿轮齿面方程的建立,分析共轭鼓形齿联轴器传动的静力学特性、动力学特性、接触强度、弯曲强度与变形,研究该传动的多齿啮合状态与性能。
5.2 共轭鼓形齿面方程的建立
要进行共轭齿面鼓形齿联轴器的啮合分析,必须首先创建共轭鼓形齿联轴器内外齿轮齿面的几何数学模型,也就是要建立内外齿轮齿面的方程。
对于共轭齿面鼓形齿联轴器,直齿内齿轮齿面方程可直接给出,根据求解共轭齿面啮合的运动学法,可求解出与直齿内齿相共轭的外齿齿面方程。
5.2.1 坐标系
坐标系如图5-1所示。

S1(0,x1,y1,z1)坐标系,为与外齿轮固连的动坐标系;z1轴与外齿轮轴线重合。
S10(0,x10,y10,z10)坐标系,为过渡坐标系;z10与z1轴重合;x10与x1夹角φ1为某瞬时外齿轮转角。当φ1=0时,S10系与S1坐标系重合。
S20(0,x20,y20,z20)坐标系,为静坐标系;z20轴与轴z2重合;x20轴与x2轴夹角φ2为某瞬时内齿轮转角,当φ2=0时,S20系与S2系重合。
四个坐标系有共同的原点O,x10与x20轴线重合,z10与z20轴线夹角为两齿轮轴线的轴交角θ(y10与y20轴线的夹角亦为θ)。
5.2.2 坐标转换关系
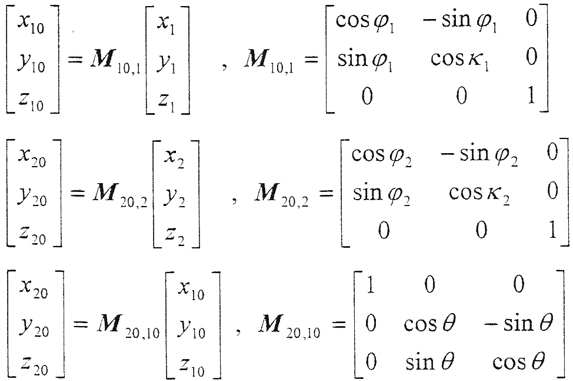
坐标的逆变换可由它们的逆矩阵导出。
5.2.3 内齿轮齿面方程
内齿轮轮齿为直齿,其端面齿形及坐标关系如图5-2所示。设端面齿廓线为渐开线,xc2坐标通过渐开线在基圆上的起点,在(o,xc2,yc2,zc2)坐标下的齿面方程为
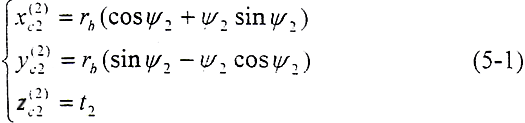
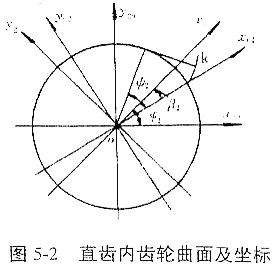
式中,φ2、t2——齿面参变量,rb——渐开线基圆半径。设a2为齿面某一点k处的压力角,则有φ2=tana2。
将(5-1)式转换到S2坐标系上,得
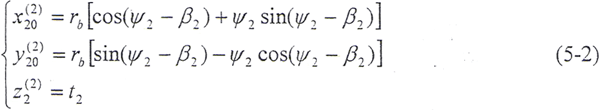
将(5-2)式转换到S20坐标系上,得
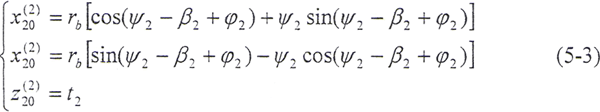
式中,β2——内齿轮基圆齿槽宽所对圆心角之半。
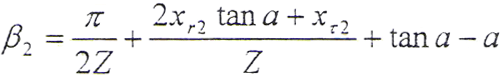
式中,α——分度圆压力角
Z——齿轮齿数;
xr2——内齿径向变位系数;
xτ2——内齿切向变位系数。
式(5-3)就是内齿轮齿面在S20坐标系中的齿面方程。
5.2.4 外齿轮齿面方程
根据求解共轭齿面的运动学法,外齿轮齿面方程为

式中,r1——外齿轮齿面方程;
r2——内齿轮齿面方程;
f(ψ2,t2,φ2)=0——啮合方程,由N·v12=0推导而来:
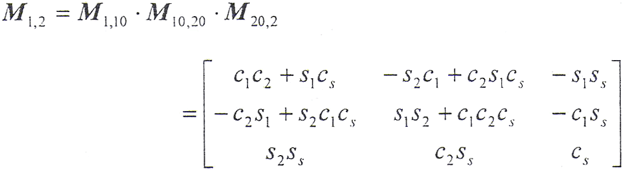
其中,
c1=cosφ1;s1=sinφ1
c2=cosφ2;s2=sinφ2。
cs=cosθ;ss=sinθ
在(0,x2,y2,z2)坐标系上,内齿轮齿面法向矢量的三个坐标分量分别为
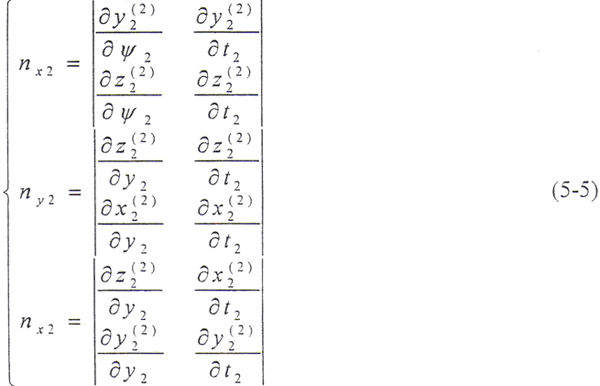
在(0,x2,y2,z2)坐标系,相对速度的三个坐标分量为

将(5-5)式、(5-6)式代入N·v12=0,得
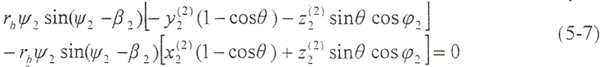
将(5-2)式代入(5-7)式,经化简得

式(5-8)即为啮合方程。
在(0,x1,y1,z1)坐标系下的外齿轮齿面方程为
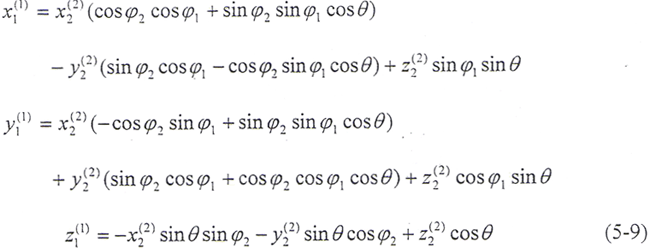
式中,φ1、φ2——内、外齿面的转角。
令φ1=φ2=φ,将(5-2)式及由(5-8)式解出的t2代入(5-9)式,即可得到以ψ2、φ为参变量的外齿轮齿面方程:
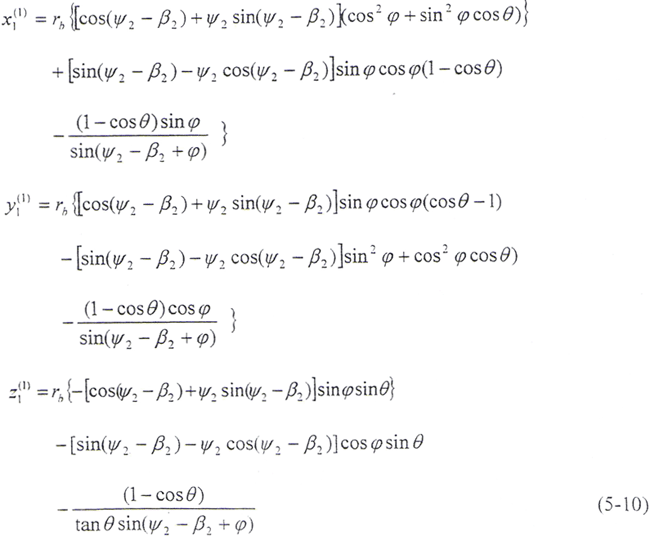
为了啮合分析方便,要给出在固定坐标系下的接触线方程,即啮合面方程。在S20坐标系下接触线方程为
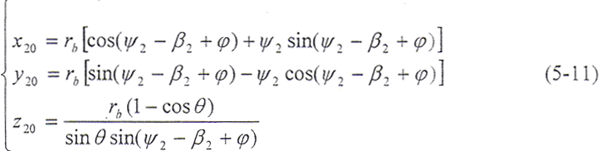
由f(ψ2,t2,φ2)=0,r2(ψ2,t2)还可给出内齿轮齿面上的接触线方程:
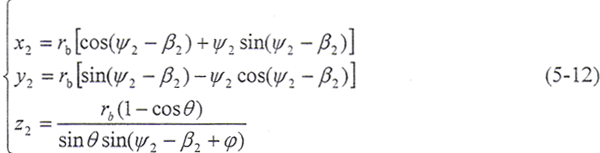
5.3 共轭鼓形齿联轴器传动力学特性分析
5.3.1 鼓形齿联轴器传动静力学分析
为了研究鼓形齿联轴器的传动特性,以便设计、加工和优化这种传动装置,必须知道该传动件上传动齿轮的工作载荷。传动齿轮的工作载荷包括静载和动载两部分,所谓鼓形齿联轴器传动的静力学分析,即暂不考虑传动中的动载荷,仅按静态情况对鼓形齿联轴器传动进行受力分析和研究。
根据鼓形齿联轴器啮合分析,在不考虑弹性变形的刚性情况下,我们认为,传动齿轮沿接触线上的法向载荷是均匀分布的,且传动齿轮各接触齿对受载相等;在考虑弹变形后,各接触齿对上的瞬时载荷的大小和分布要发生变化,其变化情况与各接触齿对在各瞬时的综合刚度系数成正比。
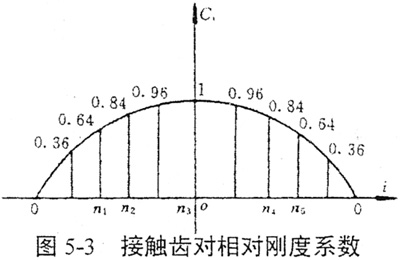
由鼓形齿联轴器多齿接触试验得知,当鼓形齿联轴器在传动过程中,各接触齿对的综合刚度系数Ci是由小变大,再由大变小,即在啮合区两端刚度系数最小,在啮合区中段的综合刚度系数为最大Cmax。因为此处只需要知道各啮合齿对在某瞬时综合刚度的相对大小,且综合刚度系数的数值都是用实测方法求得的,鉴于实验条件,为方便起见,设Cmax为单位1,并假定其他各对啮合齿的刚度系数整体副近椭圆分布规律,即
Ci=Cmax[1-(0.2i)2](i=0,1,2,…) (5-13)
式中i为接触齿对号,其各接触齿对所对应的相对刚度系数如图5-3所示。
在某瞬时,各啮合齿对的综合刚度系数之和即总体综合刚度系数,即
CΣi=ΣCi
当不考虑齿轮基节和其他制造误差时,刚度系数为Ci的那对齿所受的载荷

式(5-14)即为齿间载荷分配表达式,其中受载荷最大齿对的法向载荷

式中,Fn——总额定扭矩Mn的等效法向载荷,即

齿面上法向力Fnimax在x、y、z三个方向的分量大小分别为

式中,n0——接触齿面上的单位法线向量,即
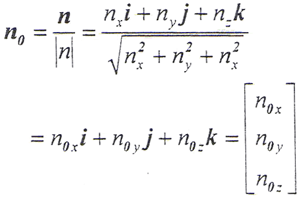
式中,n——齿面上任意点k的法线向量,即
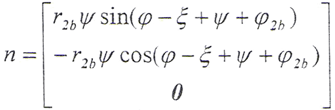
式中,φ——齿轮相对静参考系的转角;
ξ——基圆齿槽宽所对圆心角之半;
ψ——齿廓上任意点k的展角θk与压力角αk之和;
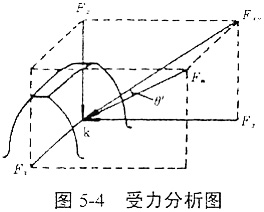
φ2b——第i对齿基圆上的点与静参考系间所夹的圆心角。其接触线上任意点k处的受力状态如图5-4所示。
5.3.2 鼓形齿联轴器传动动力学分析
鼓形齿联轴器传动装置实际上是一个弹性动力学系统,它由鼓形外齿、渐开线内齿、轴和轴上其他零件组成,对这样一个结构系统进行动力学分析是相当复杂和困难的。为了分析方便,可将弹性系统分为两部分,一是轮系部分,二是轴系部分。由于轮系轮齿的刚度远远大于轴的刚度,所以,就可以把二者分开,即当分析轴的弹性变形所造成的齿轮扭转振动时,可以认为齿是刚性的;而在分析由于齿的弹性变形引起的动载荷时,就可不考虑轴及其它零件的弹性载荷,认为传入的转距是常量。
5.3.2.1 鼓形齿联轴器传动的轮系固有频率
一轴间倾角为θ的鼓形联轴器,在传递载荷的过程中,一般有几对齿处于接触啮合状态,此时由动力学基本定理,有
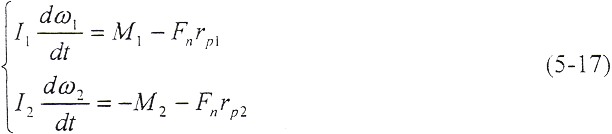
式中,I1,I2——鼓形外齿轮1和渐开线内齿轮2的转动惯量;
M1,M2——外、内齿轮单位齿宽上的扭矩;
Fn——纯翻转位置处啮合齿对单位齿宽上的法向载荷;
rp1、rp2——纯翻转位置处外、内齿面上法向载荷等效集中力作用点P的径向坐标。当鼓形齿联轴器匀速转动时,有
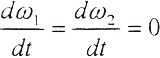
由(5-17)式,得

或

另一方面,当考虑轮齿弹性变形后,啮合齿对因沿接触线的刚度发生变化,沿接触线压力分布处于非均匀状态,其分布规律为
Fnk=Ckδk (5-19)
式中,Ck——轮齿接触线上点k处的刚度系数;
δk——轮齿接触线上点k的综合变形。在等效点P处,则有
Fnp=Cpδp (5-19a)
如果在t=0的瞬时,由于干扰载荷的作用,轮齿的变形量增大△δ,则齿上的载荷也奖增加△Fn,当转矩M1、M2为定值时,由齿轮的平衡条件可知,齿轮的角速度ω将发生周期性变化,而载荷和变形也以同一频率变化。由(5-17)式和(5-18)式,得

式中,
△Fn=Cp△δ (5-21)
由弹性啮合原理可得,两相啮合的弹性齿轮连续啮合运动的条件,即两齿靠近的速度要等于它们变形增加的速度。根据两啮合弹性齿轮连续运动的条件,有

对上式两边微分,并利用(5-20)式、(5-21)式,可得鼓形齿轮联轴器传动的自振微分方程为

即
△δ+β2△δ=0 (5-23a)
式中,

式(5-23)是一个二阶线性齐次微分方程,其一般解为
△δ(t)=Bcos(βt)+Csin(βt) (5-25)
式中,B、c——积分常数,可由p点的初始条件确定。
设在初始时刻t=0时,△δ(0)=△δ0(初位移),△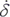 (0)=v0(初速度),则由(5-25)式,可求出
(0)=v0(初速度),则由(5-25)式,可求出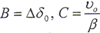 。于是,动位移的表达式可写为
。于是,动位移的表达式可写为
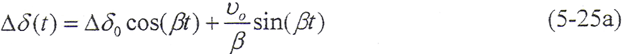
在上述分析中,可以用旋转矢量来描述鼓形齿联轴器的动位移情况。旋转矢量的模为振幅A,角速度为角频率β,如图5-5所示。
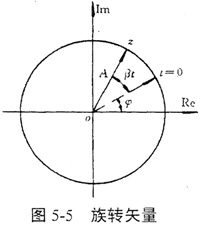
若用复数来表示,则
z=Aexp[j(βt+φ)]=Acos(βt+φ)+jAsin(βt+φ) (5-26)
式中,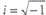 。复数z的实部和虚部可分别表示为
。复数z的实部和虚部可分别表示为

此时,动位移△δ可表示为
△δ(t)=Im Aexp[j(βt+φ)] (5-28)
其变化的速度和加速度分别为
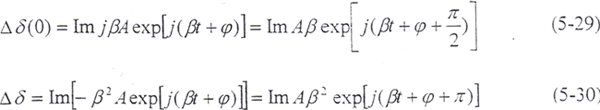
用复指数形式描述这种谐振动,给运算带来很大方便。因为复指数exp(jβt)对时间t求导一次,相当于在其前面乘以jβ,而每乘一次j,就相当于增加初位相角π/2。
轮系的固有频率则为
f=fp=βp/(2π)=β/(2π)=(Cp/md)1/2/(2π) (5-31)
式中,md为轮系的当量质量。
以上对轮系即齿轮传动的固有频率进行了分析,实际上,齿轮传动的固有频率还受许多因素的影响,如齿轮本体的轮缘、轴、齿面间的油膜厚度以及支承条件等。此处讨论系的固有频率,忽略了这些因素的影响,因此,上述轮系固有频率的计算公式具有一定的条件性,其主要目的是为了本问题讨论的系统性,以作定性分析和概念阐述。共轭鼓形齿联轴器传动的振动诱因主要来源于轴系,轴系固有频率的研究是共轭鼓形齿联轴器振动问题的重要组成部分和最具实用价值的内容。
上一页
下一页


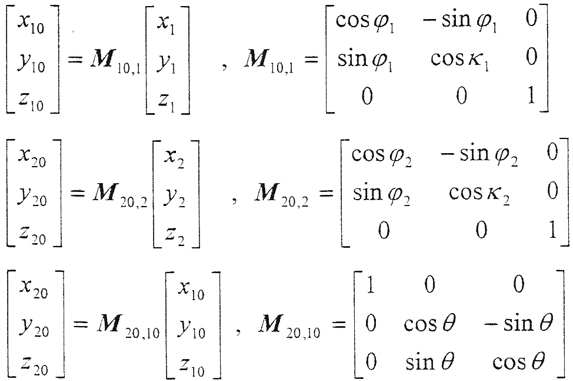
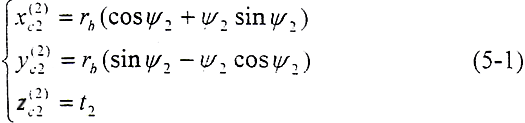

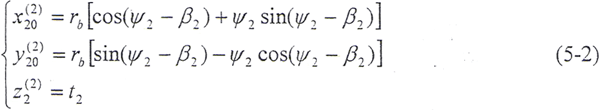
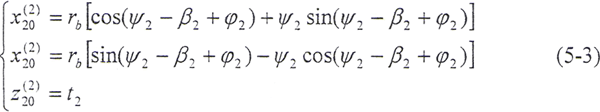
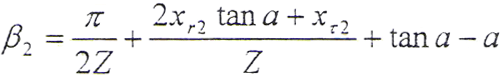

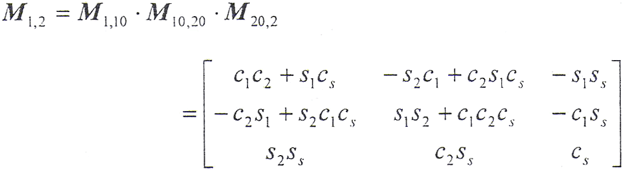
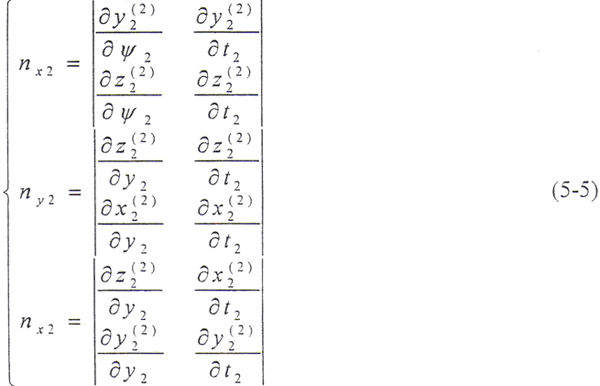

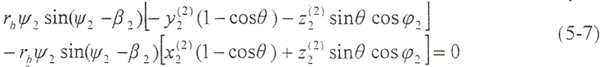

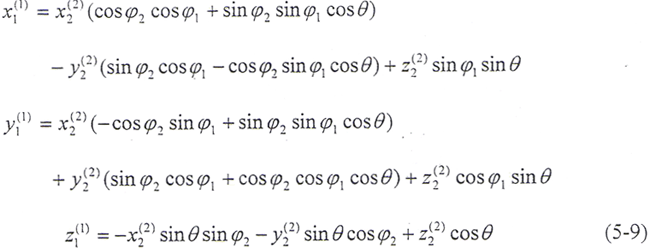
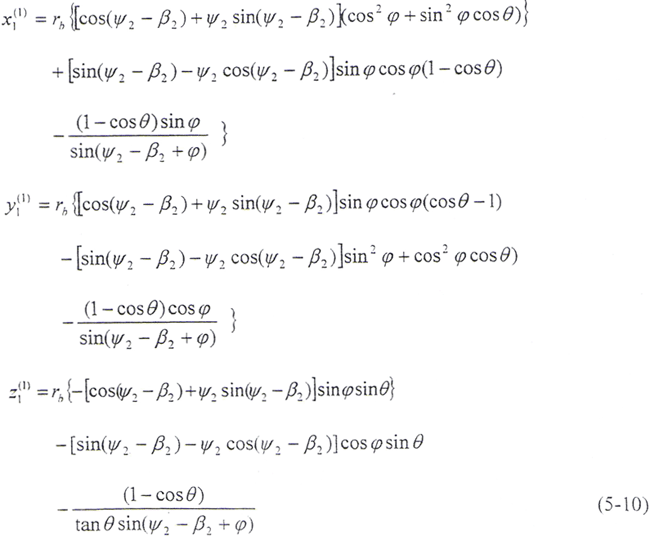
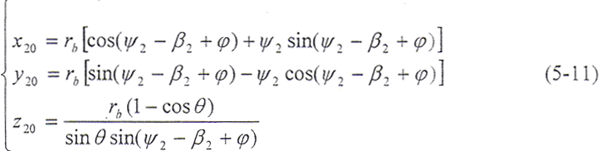
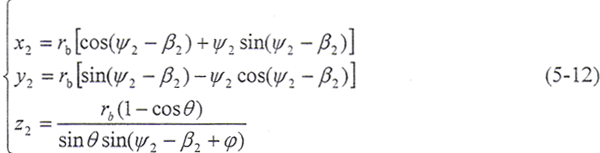





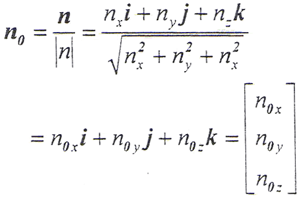
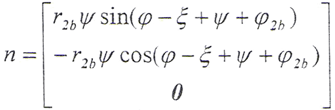

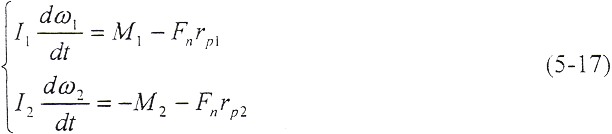






 (0)=v0(初速度),则由(5-25)式,可求出
(0)=v0(初速度),则由(5-25)式,可求出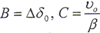 。于是,动位移的表达式可写为
。于是,动位移的表达式可写为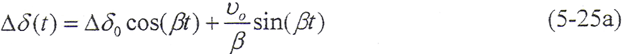

 。复数z的实部和虚部可分别表示为
。复数z的实部和虚部可分别表示为