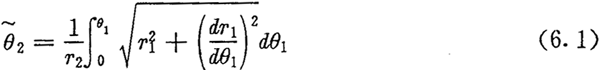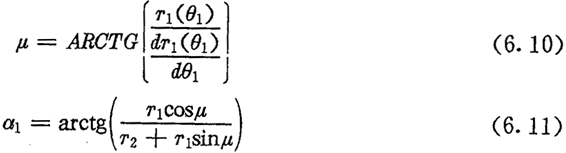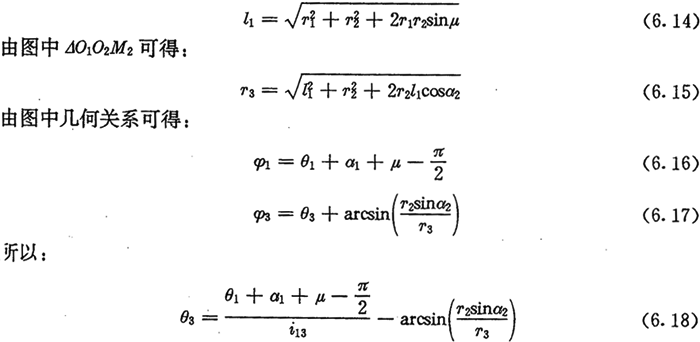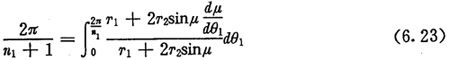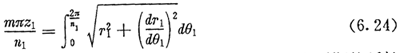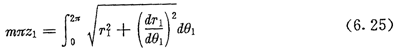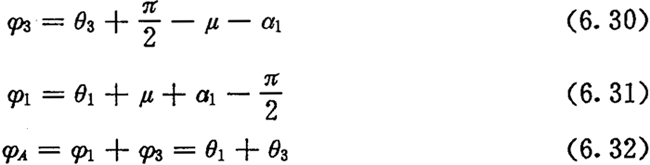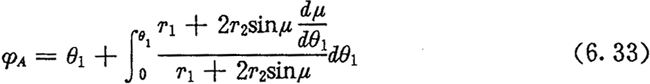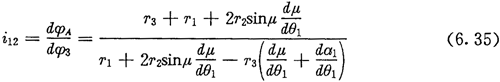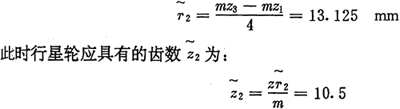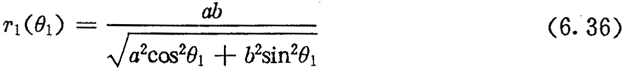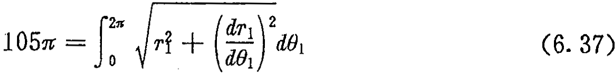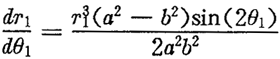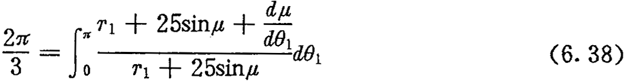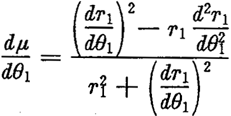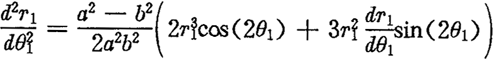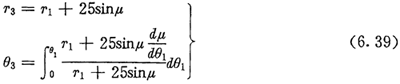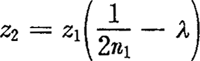6 两种有非圆轮的行星传动机构的不同设计
6.1概述
单激波推杆减速器的激波器廓形一般使用偏心圆，多激波推杆减速器的激波器廓形是非圆弧曲线。当去掉推杆，内外滚子合而为一时，推杆减速器就变成了滚柱活齿减速器，如图6.1所示。因而可以把它们都看作是非圆行星传动机构。这类活齿传动机构的瞬时传动比是个常数，如式（2.8）所示，这也是设计活齿传动机构必须遵循的准则。从后面的分析可知，这就决定了活齿传动机构各啮合副的运动性质都不可能是纯滚动。因而要在推杆两端加装内外滚子以增加滚动成份而减小滑动成份。对于滚柱活齿减速器来说，因为滚柱同时要与激波器、内齿圈相接触，所以一定有一面有滑动。因而可以说活齿传动是一种滑滚运动方式的非圆行星传动。由于运动副是滑滚运动，实际机构不能使用轮齿进行传动，而是靠相啮合的两个轮的光滑表面接触。
如果去掉瞬时传动比为常数这个前提，根据运动副都作纯滚动的运动方式，可设计出纯滚动的非圆行星齿轮传动机构（图6.2）。从后面的分析可知，这种机构，相邻两行星轮之间的中心角是变化的，相邻行星轮和太阳轮、内齿圈之间所包容的面积也是变化的，利用这一特性，可制造出低速大扭矩液压马达。
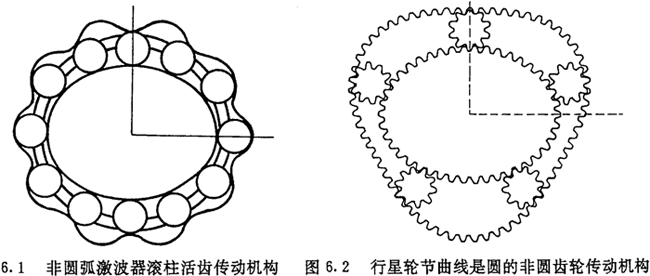
心角的变化规律进行了分析。
6.2节曲线之间的关系
设太阳轮节曲线方程为T1= T1（θ），行星轮节曲线是半径为T2的圆，根据机构作纯滚运动或瞬时传动比为常数这两种不同的设计原则，可设计出两种不同的内齿圈齿廓曲线。
6.2.1纯滚动运动方式的节曲线关系
建立如图6.3所示的坐标系，在起始位置，分别与太阳轮、行星轮以及内齿圈固联的三个动坐标系的极轴x1、x2、x3在同一条直线上，且指向相同。图6.3所示为太阳轮相对行星轮转过了φ1角的情形。设此时内齿圈相对该行星轮转过的角度为φ3，根据三心定理，作平行平面运动的三个构件的三个瞬心必然位于同一条直线上，而纯滚动副的接触点就是它们的瞬心。因而太阳轮与行星轮节曲线的接触点M1，行星轮与内齿圈节曲线的接触点M2以及传动中心O1这三个点位于同一条直线上。因为是纯滚动，图6.3中弧长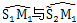
应相等（在起始位置S1与S2重合）。由此可得图6.3中
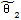与θ1的函数关系为。
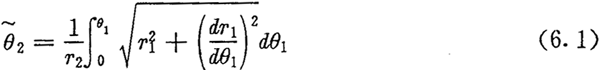
设μ为太阳轮节曲线在M1点的切线正向与矢径O1M1的夹角，由微分几何知：
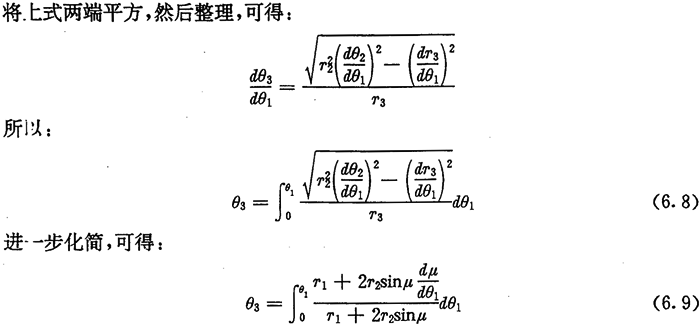
将（6.5）式及（6.9）式联立，便是内齿圈节曲线的方程。同理，若已知内齿圈节曲线方程，仿上可求得太阳轮节曲线。
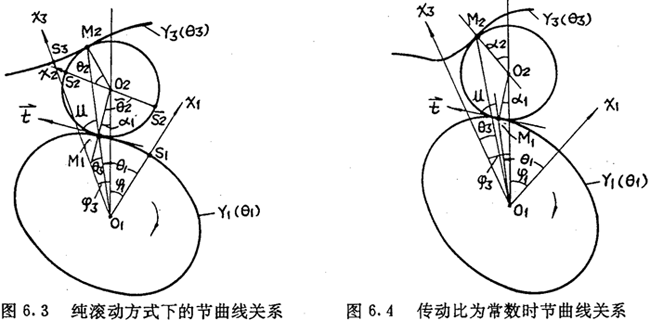
6.2.2按传动比为定值的设计
如图6.4所示，设太阳轮相对行星轮从初始位置转过φ1角时，内齿圈相对该行星轮反向转过的角度为φ3。令φ1与φ3的比值为常数i13，这时上一节中弧长相等的特性已无法保证，因而接触点M1、M2也不再是运动的瞬心，M1、M2及中心O1不一定在同一条直线上。这就是滚柱活齿传动的结构形式。设计方法与第二章类同。现简要叙述如下：
曲线向径与切线正方向的夹角μ以及工作角a1的计算都与纯滚动动方式下相同，即：
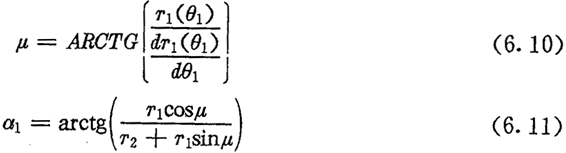
由（2.16），行星轮工作角α2及α1之间有关系式
即
若用l1表示行星轮与太阳轮的中心距O1O2，则由图6.4可得：
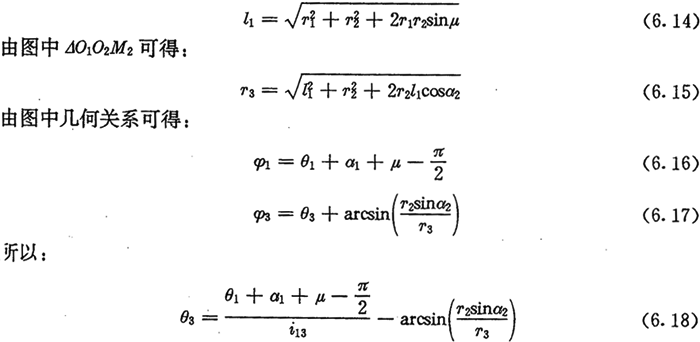
联立（6.15）式及（6.18）式，便是内齿圈的齿廓方程。内齿圈的齿廓曲线是行星轮节曲线的外包络线。
从上述求内齿圈齿廓方程的过程可以看出，由于规定了转角φ1与φ3的比值为常数i13，使得对于太阳轮的任一转角φ1，φ3相应地有确定的值φ3=φ1/i13。同时图6.4中行星轮工作角α2也随之由（6.12）式确定下来。因而M1、M2与O1三点肯定不会始终保持在同一条直线上。其理由如下：
假设图6.4中O1、M1、M2三点始终都能保持在同一直线上，则对于太阳轮转角φ1，图6.4中的α2可根据图6.3中的行星轮转角θ2求得，由图中几何关系及（6.4)式应有
另一方面，由于φ1与φ3的比的比值为常数i13，α2的值已由（6.12）式确定。比较(6.19)式与（6.12）式可知，只有在α1=0且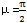
时，它们才是一致的，由（6.10）式及（6.11）式知，只有在
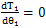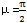时才有，且α1=0，由于太阳轮的节曲线是周期性，所以在一周内只有2n1个点（nl是太阳轮节曲线的周期数）有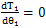，其余各点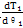
都不为零，对于太阳轮的转角φ1只要不是对应于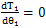，式（6.19）与式（6.12）是矛盾的，也就是说M2点必然不会与M1、O1位于同一直线上。这说明当传动比为常数时，行星轮与太阳轮、行星轮与内齿圈所组成的两个啮合副不可能都作纯滚运动，一定有一个啮合副有滑动，因而活齿传动都是滑滚运动。
6.3节曲线的封闭条件及等分
对于作纯滚运动的非圆行星齿轮传动机构，上面求得的节曲线关系只是一般的公式，要设计出实际的非圆行星齿轮传动机构还要受到许多限制。
6.3.1节曲线的封闭条件
为了能够连续转动，已知的太阳轮节曲线当然应是连续而封闭的,T1(θ1）必须是θ1的周期函数。设太阳轮一转中的周期数是n1，当太阳轮相对行星轮从θ1= θ10转过一个周期时，由于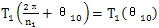
，所以由（6.2）式可知转动前后在接触点具有相同的μ值。根据（6.4）式，设θ1=θ10时，行星轮的转角有关系式
则当太阳轮相对行星轮转过一个周期后，由于μ值相同，行星轮转角关系式为：
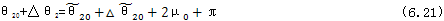
上式中△θ2及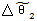
分别为行星轮转角θ2及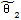在太阳轮从θ1=θ10转过一个周期后的增量。由（6.20）式和（6.21）式可知在太阳轮转过的任一周期中，行星轮转角增量△θ2与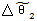相等，即：
由此可得到结论：太阳轮节曲线在一个周期内的弧长与内齿圈节曲线在一个周期内的弧长相等。若内齿圈的周期数为n2，则n2应大于n1。为了减小行星轮尺寸，应取最小整数值n1+1作为内齿圈节曲线的周期数，从而可由（6.9）式得到内齿圈节曲线的封闭条件为：
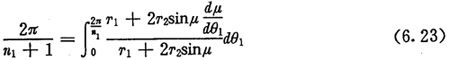
6.3.2节曲线上轮齿等分的限制
设齿轮的模数为m，为了使太阳轮、行星轮及内齿圈都有等分的轮齿，它们的节曲线都必须是周节mπ的整数倍。由上节知道，太阳轮节曲线与内齿圈节曲线在一个周期内的弧长相等，并且内齿圈的周期数比太阳轮的周期数大1，所以内齿圈节曲线的周长是太阳轮节曲线周长的（n1+1）/n1倍。因此只要太阳轮节曲线在一个周期内的弧长能够被周节等分，就能保证内齿圈的等分。也就是说，设z1为太阳轮齿数，则z1应是n1的整数倍，且太阳轮与内齿圈的轮齿等分条件为：
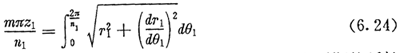
由于每个周期的弧长都是相等的，太阳轮节曲线的总长等于n1个周期的弧长之和，用n1乘以（6.24）两边，可得等分条件的另一种表达形式：
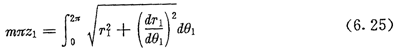
对于节曲线为圆的行星轮，轮齿等分条件为：
2T2=mz2 （6.26）
上式中z2为行星轮的齿数，显然内齿圈齿数z3为：
6.3.3不干涉条件
设计的非圆行星齿轮传动机构还应保证太阳轮最大向径处的齿顶与内齿圈录小向径处的齿顶不发生相碰。若太阳轮节曲线在θ1=0时向径取得极小值，则内齿圈节曲线向径的极小值为T1（0）+2T2，对于关于极轴有对称性的太阳轮节曲线，在θ1=π/n1时有极大向径，若齿顶高为ha，则不发生运动干涉的条件为：
6.4传动特性分析
6.4.1太阳轮与行星轮的平均传动比
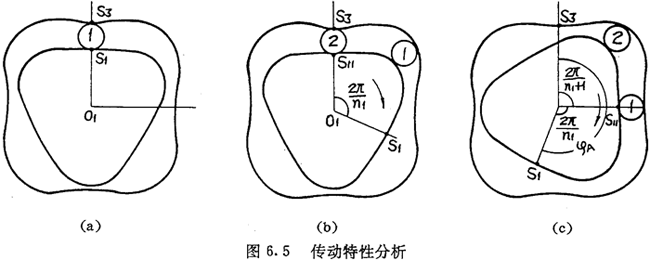
固定内齿圈，当太阳轮起点从初始位置开始转动到与行星轮重新在初始位置接触时，太阳轮转过的圈数与行星轮公转过的圈数之比ip12称作太阳轮与行星轮的均传动比。图6.5(a）为初始位置，图6.5(c）为太阳轮按顺时针方向相对行星轮1转过一个周期后的情形。此时内齿圈相对该行星轮也应转过一个周期，即行星轮1从初始位置公转过的角度为：
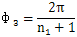
而太阳轮相对内齿圈转过的角度φA为：
即太阳轮转两圈零一个周期，行星轮公转一圈。
6.4.2行星轮的个数
设太阳轮起点从初始位置相对内齿圈转过一个周期，从图6.5(a）转到图6.5(b）位置。从图6.5(b）可知，此时在内圈的初始位置S3处可放入另一个行星轮，称它为2号行星轮。类似当太阳轮从初始位置相对内齿圈转过第二个周期，在S3可放入第3号行星轮，太阳轮旋转一圈，放入第n1+1号行星轮，太阳轮转两圈，放入第2nl+l号行星轮，当太阳轮转两圈零一个周期，恰好第1号行星轮回到S3点。所以可安放的行星轮总数为2n1+1个。
6.4.3相邻两行星轮之间的中心角
设太阳轮起点从初始位置相对内齿圈顺时针转过了φA角，当φA大于太阳轮一个周期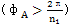
时，第2号行星轮也相对内齿圈极轴公转过了一个角度（图6. 5（C））。令
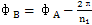，则φB表示此时太阳轮与2号行星轮的初始接触点S11相对内齿圈初始位S3转过的角度。用φ3表示1号行星轮相对内齿圈初始位S3公转过的角度，由图6.3可得：
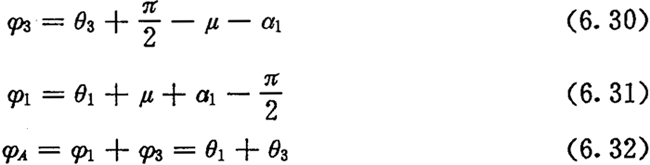
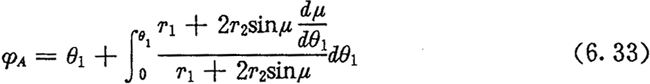
根据（6.33）式，可由任给的φA确定出太阳轮起点S1至1号行星轮与太阳轮节曲线的接触点M1所来的中心角θ1，然后代入（6.30）式，可得l号行星轮中心O2与内齿圈初始件S3所夹的中心角φ3(φA)。用φB代替（6.33）式中的φA，将解得的θ1值代入（6.30）式，便可得到第2号行星轮中心与内齿圈S3点所夹的中心角φ3(φB)。两行星轮之间的中心角ψ为：
可见两行星轮所夹的中心角ψ是太阳轮相对内齿圈转角φA的函数，它随着φA值的不同而呈周期性的变化，并围绕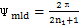
上下波动。太阳轮与行星轮的瞬时传动比i12为：
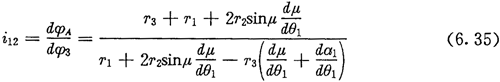
i12也是随太阳轮转角φA变化的函数。由于太阳轮和内齿圈都是非圆的，而相邻两行星轮之间的中心角又是变化的，因而太阳轮、内齿圈与相邻两行星轮之间包含的面积也是变化的，正是利用这些特性，可制造出低速大扭矩液压马达、空气压缩机等机器。
6.5设计步骤及计算实例
现以太阳轮是一个回转中心在几何中心的标准椭圆为例，来说明纯滚动非圆仃虽传动非圆行星传动机构的设计方法步骤。
给定齿轮模数m=2.5,n1=2，内齿圈周期数为3 ，设计步骤如下：
6.5.1确定齿数
太阳轮的齿数z1可根据所要求的太阳轮的大小来确定，它应是n1的整数倍。本例选z1=42，由（6.27）式，内齿圈齿数应为z3=63。为了确定z2的合适数值，可以采用这样的方法，假想太阳轮和内齿圈都退化成齿数为z1及z3的圆齿轮，则此时的行星轮半径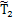
应为：
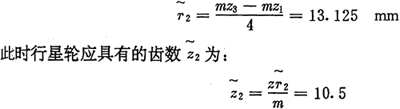
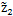时常不是整数，我们称它为行星轮的参考齿数。实际采用的太阳轮虽然和退化的圆齿轮具有相同的模数m和齿数z1，但是它的形状不是圆的，这就使得实际采用的行星轮齿数z2应比参考齿数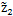小，太阳轮节曲线与圆相差越大，z2应比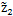小的越多。为了减小轮齿干涉的可能生，z2要尽量接近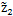。本例选z2=10，从而得T2=12.5mm。
6.5.2确定太阳轮节曲线
所要求的椭圆型太阳轮节曲线方程可表示为：
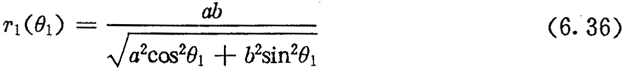
上式中，a为椭圆的长轴半径，b为椭圆的短轴半径。由（6.25）式得轮齿等分条件为：
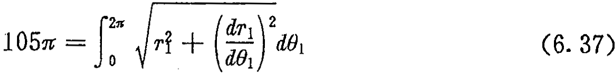
上式中的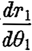
可由（6.36）式求得
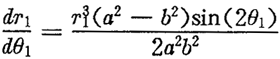
由（6.23）可得节曲线封闭条件为：
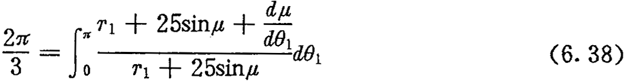
上式中μ按（6.2）式计算，而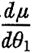
由（6.2）求得为：
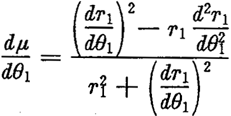
其中：
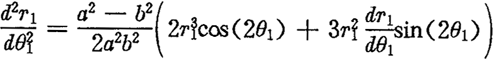
利用辛普生法计算数值积分，由（6.37）和（6.38）两条件式组成的方程组可解算出参数a和b来，结果是：
a=59.7616 mm b=44.6943 mm
取ha=2.5，将T1（0）=44.6943，T1（π/2））=59.7616，T2=12.5代入（6.28）式，可知不会发运动干涉。
6.5.3求人齿圈节曲线
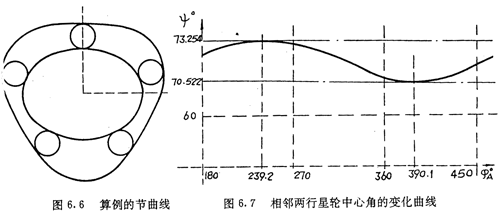
根据（6.5）式和（6.9）式，可得内齿圈节曲线方程为：
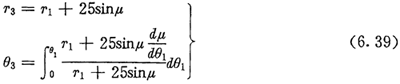
节曲线形状如图6.6所示。图6.2为该轮系加上轮齿后的情形。按（6.34）式可算得相邻两行星轮之间的夹角随φA的变化规律，其关系曲线如图6.7所示。由曲线图可看出，当φA=239.2°时，夹角ψ有最小值ψmin=70522°，夹角ψ的变化范围是2.732°。
6.5.4机构优化
从以上设计过程可以看出，根据非圆太阳轮设计行星轮为圆的纯滚动非圆行经齿轮传动机构时，并不是对任意指定的太阳轮节曲线都有解。当太阳轮节曲线的周期数n1给定后，节曲线必须有两个可调整的参数（例中的a和b）的要由节曲线的封闭条件及轮齿等分条件来确定。齿轮模数m和太阳轮齿数z1是被预先指定了的。当各参数求出后，要用不干涉条件（6.28）式进行校验，若发生干涉，应调整z1数值，重新计算太阳轮的可调整参数。
显然，当太阳轮与圆的差别越大时，越容易发生运动干涉。液压马达、空气压绷机等机器正是利用了相邻两行星轮之间的中心角变化的特点，当太阳轮与圆的差别越大时，相邻两行星轮之间夹角的变化范围也越大，这是液压马达等机构所要求的。
令：
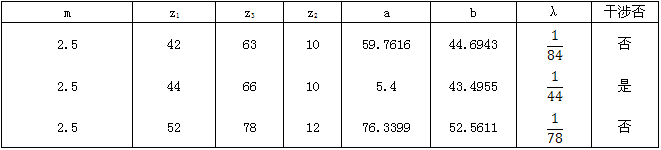
λ反应了非圆行星传动机构与圆行星传动机构的差别程度，当λ=0时，非圆行星传动机构就变成了圆行星传动机构。λ越小，越不容易发生运动干涉，λ越大，相邻两行星轮之间中心角变化的范围也越大。表（6.1）给出了在齿轮模数m相同的情况下，椭圆形太阳轮取不同的齿数z1时，按上述设计步骤得到的结果。因为：
表6.1 椭圆太阳轮取不同齿数时的计算结果
所以当z1不能被2n1整除时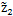，就不是整数。由（6.41）式和（6.40）式可得：
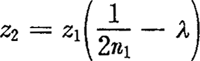
将上式代入不干涉条件式（6.28）后，可得
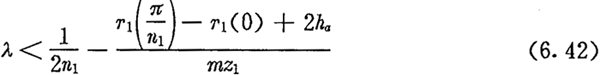
为了得到机构不发生运动干涉时的最大λ值，将（6.42）式中的小于号换成等号，并将λ代入，对于椭圆形太阳轮，得到下面等式：
mz2=a-b+2ha (6.43)
从（6.37）、（6.38）、（6.43）三式所组成的方程组中，解出a、b及z2，将齿数代入( 6.40)便得到临近发生运动干涉时的λ值。因为z2是整数，当m给定后，由上面三个式子所组成的方程组一般是无解的。若把m也作为一个参变数，这时方程有解。
在进行具体机构的设计时，齿轮模数m都是指定的。根据所要求设计的机构体积的大小可事先指定一个太阳轮齿数z1的取值范围，若以相邻两行星轮之间中心角变化的范围最大为优化设计目标，按上述设计方法，并加上不干涉条件的限制．则可在所规定的z1取值范围内得到最佳结果。
上一页
下一页
