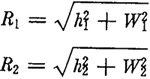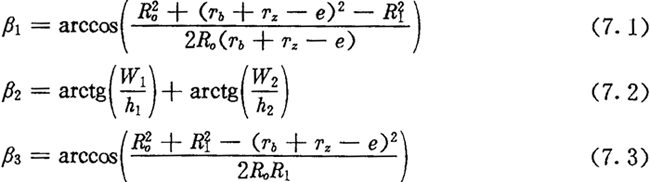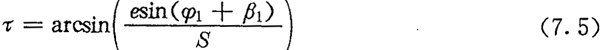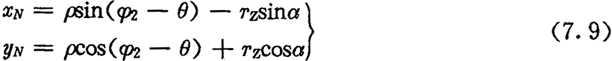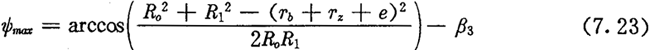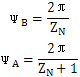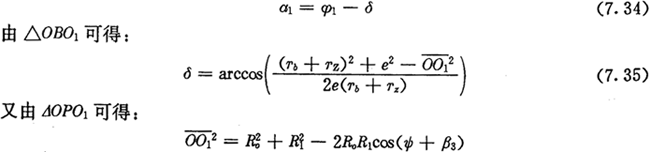7 新型摆杆减速器的研究
7.1概述
摆杆减速器是一种新近提出的活齿减速器结构类型，它把沿传动圈导槽移动的推杆变成了绕固定轴销摆动的摆杆，使减速器中各运动副的相对运动都成为转动，从根本上解决了现有推杆减速器移动副严重磨损的问题。和现有的推杆减速器或滚柱活齿减速器相比，在保持原有优点的基础上，使啮合效率得到了进一步提高，是活齿减速器中较理想的一种结构形式。
文献只提出了摆杆活齿传动的一般结构方案，要把这种方案变为实际产品，还有许多理论问题需要解决。例如对机构传动特性的分析，效率计算，强度校核，以及内齿圈齿廓的测量等等。本章从摆杆减速器的传动原理着手，对这些问题进行了详细的分析讨论，为摆杆减速器的制造奠定了理论基础。
7.2 结构组成及齿廓方程式
7.2.1结构组成
图7.1所示为摆杆减速器的结构简图。摆杆减速器也由四大部分组成：激波器1；摆动机构（包括摆杆2，内滚子6, 外滚子5和轴销7)；传动圈3 以及与其固联的输出轴8；内齿圈4。可以看出，除了摆动机构外，其它构成与推杆减速器类似。也采用了两套完全相同且互成180°的激波器及内齿圈以实现输出的静平衡和提高啮合效率。
传动中，摆杆内滚子6受到激波器驱动，而外滚子5 则与内齿圈啮合，摆杆绕轴销7摆动的同时，传动圈及输出轴转动，从而完成了转速的变换及功率的传递。
摆杆减速器的瞬时传动比为常数，其传动比计算完全与推杆减速器传动比的计算公式相同。
7.2.2激波器转角与摆杆摆动角的关系
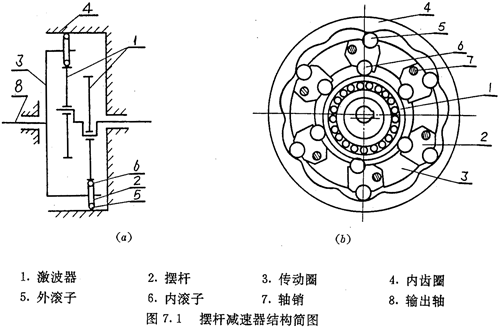
图7.2（a）所示为激波器与摆动机构所处的初始位置，此时摆杆内滚子与偏心圆激波器的短轴端点相切接触。O是激波器的回转中心，P是摆杆的摆动中心，O1及O2分别是内外滚子中心。记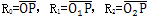
，则它们在机构转动过程中都是不变的常量，并且：
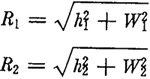
上式中h1、h2、W1和W2都是摆动中心与内外滚子中心相对位置的参数，见图7.2（a）。
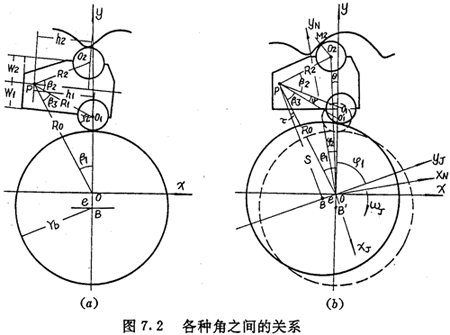
若仍记激波器半径为Tb，激波器偏心距为e，滚子半径为Tz，则由图7.2（a）可得：
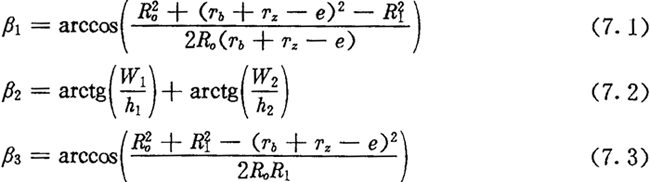
从上面各式可以看出，β1、β2及β3都是仅和机构尺寸参数有关而与转角无关的常量。
假设传动圈固定，当激波器在驱动力矩作用下从图7.2（a）所示初始位置按顺时针方向转过φ1角时，激波器与摆动机构相对位置如图7.2(b）所示。摆动中心P点在固定坐标系（o，x，y）中的位置不变，而摆杆相应地摆过了角度ψ。由图7.2(b)中△BO1P可得ψ与φ1的关系式为：
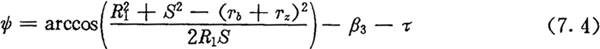
上式中，S为P点至激波器几何中心B点的距离：
而τ是有向角，如图7.2（b）所示，当激波器几何中心B点与内滚子中心O1点分别位于直线OP两侧时，τ＞0，位于同侧时，τ＜0
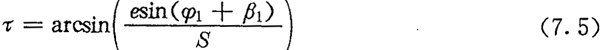
7.2.3内齿圈的齿廓方程
如图7.2(b）所示，设在激波器相对传动圈顺时针转过φ1角的同时，内齿圈相对传动圈逆时针转过的角度为φ2。对单激波来说，φ1=zNφ2，用ρ表示激波器回转中心O至摆杆外滚子中心O2的距离，由图7.2(b）中△OO2P可得：
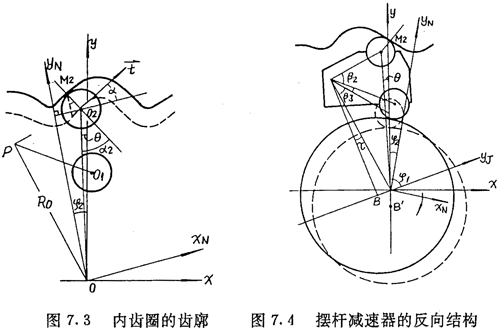
内齿圈齿廓是外滚子中心轨迹的外法向等距线，如图7.3所示，由图可得内齿圈齿廓与外滚子接触点M2在（o，xN，yN）坐标系下的的坐标为：
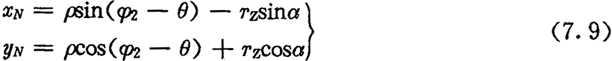
上式中，α为内齿圈齿廓在M2点的法线与yN轴的夹角，它等于外滚子中心轨迹在O2点的切线正向与xN轴正向的夹角（图7.3）
在进行具体计算时，由（7.10）式表示的α取值范围在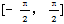
之内，只能使整个齿廓曲线的一部分由方程式（7.9）正确表示。为了使齿廓上所有的点都能用方程式（7.9）来正确计算，α的表示式应为：
当激波器按逆时针方向转动时，按顺时针方向转动时的工作齿廓成了非工作齿廓，非工作齿廓成了工作齿廓。由于工作齿廓和非工作齿方是不对称的，所以正反转（激波器按顺时针或逆时针方向旋转）的特性也是不同的。
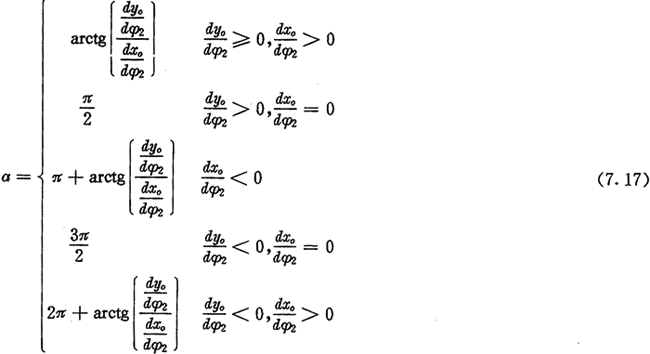
和推杆减速器一样，当理论摆动机构数目比内齿圈齿数少，即ZC=ZN-1时，机构成为图7.4所示的反向结构，在此结构中，摆杆外滚子中心在与内齿圈固联的坐标系（o，xN，yN）中的轨迹方程是：
7.3传动特性分析
7.3.1摆杆摆动的幅度
由图7.2可知，当激波器转角φ1=0时，摆杆处理初始位置，即摆动角度ψ=0，此时激波器回转中心O至内滚子中心O1的距离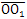
为：
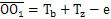
当激波器从图7.2（a）所示初始位置顺时针转过一个角度φ1时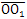，的长度也随之发生变化。分析图7.2（a）可知，当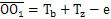时，摆杆摆动角ψ取得极大值ψmax，此时由余弦定理可得到：
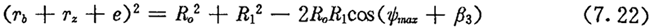
由上式及（7.2）式可得
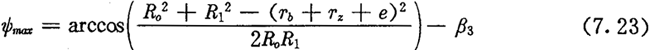
若把此时对应的激波器转角φ1记作φlm，则：
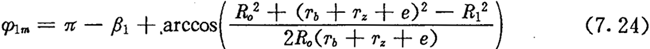
由上可知，φlm及ψmax是仅与机构组成尺寸参数有关的量。当激波器转角φ1从φlm继续旋转时，ψ便随之从ψmax减小，即摆动机构向内回摆，从而完成一次往复摆动。由摆动机构的运动性质决定了与外滚子相共轭的内齿圈的工作齿郭及非工作齿廓是不对称的。
7.3.2不发生顶切的条件
设k2为外滚子中心轨迹曲线的相对曲率，将（7.8）式中的xo、yo代入（2.23）式，并整理后可得
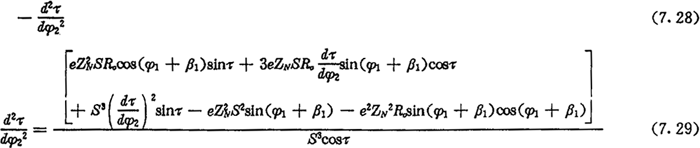
由于内齿圈齿廓曲线在齿顶处的曲率半径最小，所以当外滚子中心轨迹曲线在齿顶处的曲率半径小于外滚子半径Tz时，齿廓曲线在齿顶附近将发生项切，由此可得不发生项切的条件为
7.3.3同时工作的摆动机构数目
与推杆减速器类似，摆杆减速器的摆动机构只有从内向外摆动时才传递动力，把摆动机构从啮合传力开始到啮合传力结束推动传动圈相对内齿圈转过的角度叫做摆动机构工作区域角，记作φ2m，可表示为
摆动机构完成一次工作循环随传动圈相对内齿圈转过的角度为摆动机构工作区域角与非工作区域角之和，它等于内齿圈相邻两个齿所对应的中心角，记作ψB，用ψA表示传动圈上相邻两个摆动中心（抽销）所夹的中心角，则ψB与ψA之差体现了相邻两摆动机构中心相对 对合初始位置的差异。从而，同时工作的摆动机构数目ng为：
若摆杆减速器理论摆动机构数Zc与内齿圈齿数有关系式Zc=ZN＋1，则：
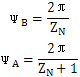
同时工作摆动机构数目为
在前面讨论的推杆减速器中，推杆的工作区域角及非工作区域角是相等的，在内断圈齿廓既不进行修形又无顶切的理论情况下，工作推杆数为推杆总数的一半。而在摆杆减速器中，摆动机构的工作区域角与非工作区域角并不相等，其工作区，或角由式（7.31）及式（7.24）确定，因而即使在内齿圈齿廓既不进行修形又无顶切，自理论情况下，工作摆动机构数目也不再是摆动机构总数的一半。根据激波器转向的不同，工作摆动机构数目可能会超过总数的一半，也可能会少于总数的一半。
[算例]
给定摆杆减速器的下列参数：
Tb=55mm e=5mm Ro=87mm Tz=10mm ZN=11
ZC=12 W1=W2=18mm h1=20mm h2=25mm
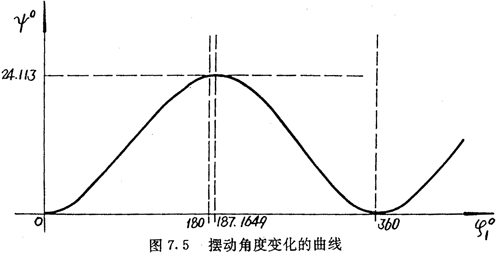
按上述公式得到齿廓曲线如图7.1（b）所示。摆角ψ随激波器转角φ1变化的曲线如图7.5所示。
按式（7.23）计算得到φmax=24.113°，按式（7.24）计算得到φlm=187.1649°，由式（7.33）计算得ng=6.24
若按机构反转计算，可得：ψmax=24.113°，φlm=172.8351°, ng=5.76
7.4效率计算
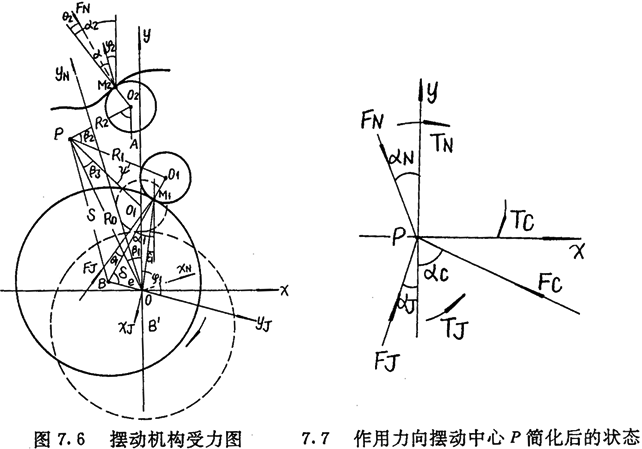
7.4.1摆动机构受力分析
固定传动圈，对于正向机构，当激波器顺时针方向转过φ1角时，内齿圈按逆时针方向转了φ2角，如图7.6所示。内滚子与激波器接触点M1处的法线与固家坐标系（o，x，y）的y轴夹角α1为：
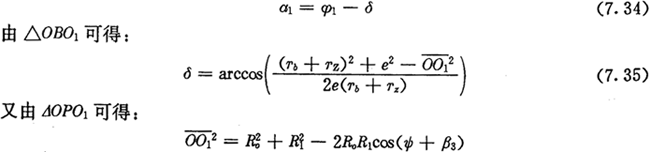
故可得：
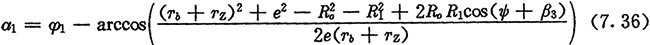
摆动机构外滚子与内齿圈齿廓接触点M2处的法线与固定坐标系（o，x，y）的y轴夹角α2为：
α2=α+φ2
上式中α的表达式为（7.17）式。
设θ1是内滚子与激波器之间的摩擦角，则激波器对内滚子的全反力FJ与固家坐标系（o，x，y）的y轴夹角αJ为：
αJ=α1+θ1 （7.37）
力FJ与PM1的夹角为∠PM1O1+θ1，由△PM1O1可得：
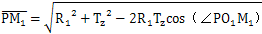
而∠PO1M1就是∠PO1B，可由△BPO1求出为
力FJ对于摆动机构的摆动中心P点的扭矩TJ是逆时针方向，数值为：
设θ2是外滚子与内齿圈之间的摩擦角，则内齿圈对外滚子的全反力FN与固定坐标系（o，x，y）的y轴夹角αN为：
αN=α2-θ2 （7.42）
力FN与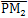
的夹角为∠PM2O2-θ2由△PM2O2可得：
上一页
下一页
