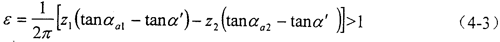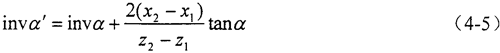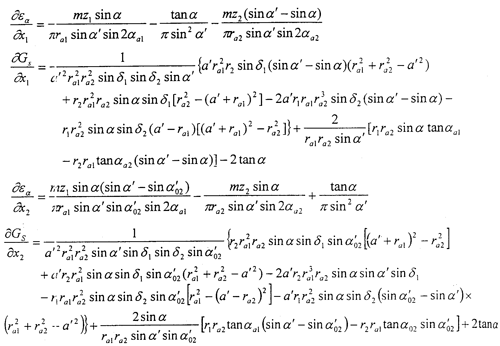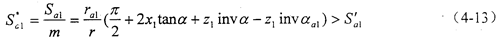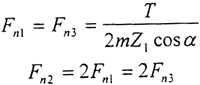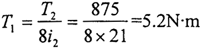第4章 三环减速机的设计
4.1引言
三环减速机是在少齿差行星传动的基础上,为了适应现代机械设备对传动装置的要求而诞生的新型减速机。三环减速机由于其原理的独特性,因而对于它的设计也提出了新的适应性要求。本章在前述理论分析的基础上,对三环减速机的设计进行了研究,力求在传动结构和技术参数上,使三环减速机的优越性得以充分实现。
三环减速机的设计包括两个关键部分一少齿差内啮合部分和均载装置部分的设计。对于少齿差内啮合部分,主要是啮合的内、外齿轮变位系数的确定,本章推导了用插齿刀加工的少齿差内啮合变位系数的牛顿迭代公式,较好地解决了这个问题;对于均载装置部分,主要是均载形式的确定和对该种形式的研究,第三章提出一种金属弹性均载环作为三环减速机的均载装置来实现均载和减振,并对均载环进行有限元和动力学分析,验证其具有适宜的刚度、足够的强度、能够满足位移均载的要求;三环减速机属于行星传动装置,因而它的安装也要满足行星传动装配条件,本章将对三环减速机的装配条件进行深入的探讨。本章还对三环减速机的两个关键零件一内齿环板和偏心套进行有限元应力分析,指导进行合理的设计。三环减速机的设计还包括其它一些部分一箱体部分、输入输出轴部分等等,限于篇幅,这些部分在本章中不加以讨论。
三环减速机的两个关键零件一内齿环板和偏心套的加工也是不容忽视的问题,由于三片内齿环板必须同时插齿加工且满足180°相位差,因此要求内齿环板工装要有准确的定位;偏心套是三环减速机的薄弱环节,它的制造也应引起足够的重视。限于篇幅,三环减速机的制造在本章中不加以讨论。
4.2三环减速机的设计
4.2.1少齿差内啮合的两个主要限制条件
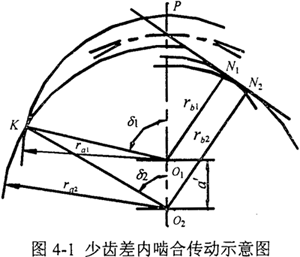
少断差内啮合传动是指内、外齿轮的齿数差较少的一种行星传动形式,它具有传动比大、体积小、重量轻、加工方便等优点,日益广泛地应用于国防、矿山、冶金、化工、纺织、起重运输、建筑工程、食品工业和仪表制造等部门和行业中。少齿差内啮合传动示意图如图4-1所示。
在设计内啮合齿轮传动时应注意如下几点:
1.为了保证渐开线齿廓,内齿轮的齿顶圆必须大于基圆,即
da2≥db2 (4-1)
2.为了避免轮齿的磨损,内齿轮的齿顶不得变尖,齿顶厚度必须大于(025~0.4)m,即:
Sa2>(0.25~0.4)m (4-2)
3.切制内齿轮时必须避免范成顶切和径向切入顶切现象
4.必须保证内啮合齿轮副的重合度ε>1。即
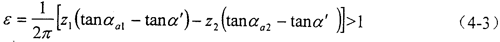
5.必须保证不产生齿顶干涉和齿廓重迭干涉,应使GS>O。即

少齿差内啮合传动由于内、外齿轮的齿数差少,易于产生各种干涉。在设计和实际使用中只需满足以下两个主要限制条件:
1.按啮合中心距a′装配时,保证齿轮副不产生齿廓重迭干涉;即应满足齿廓不重迭干涉系数GS>GS′。
2.保证获得足够的重合度,即应使齿轮副的重合度εa>εa′。
其中εa′,GS′分别为设计要求的少齿差内啮合的重合度和齿廓不重迭干涉系数。
4.2.2少齿差内啮合变位系数的确定
在少齿差内啮合传动中,目前使用最广泛的行星齿轮和中心齿轮的加工方法是范成法。外齿轮大都采用螺旋形的齿轮滚刀在Y38型或Y312型滚齿机上切制而成。内齿轮通常是采用插齿刀在Y54型或Y58型插齿机上插制而成。
变位系数的确定是少齿差内啮合传动设计的关键。文献中所述的内、外齿轮都按滚齿加工的计算公式推导出的变位系数的迭代公式,与内齿轮插齿、外齿轮滚齿的实际加工情况不一致,虽然能够保证给定的重合度和齿廓不重迭干涉系数的要求,但是不能保证标准顶隙,而且一般得出的啮合角也比较大。本章推导了少齿差内啮合传动实际加工情况的变位系数的迭代公式,解决了上述问题。
少齿差内啮合传动的两个主要限制条件是否满足,取决于齿轮的有关参数,这些参数包括齿数z0,z1,z2、齿形角α、齿顶高系数ha*,ha0*、顶隙系数c*、变位系数x0,x1,x2等。由内啮合齿轮副的无齿侧间隙啮合方程:
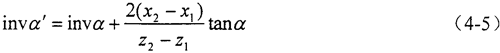
式中 α——齿形角,一般取α=20°;
α′——啮合角;
z1、z2——分别为外、内齿轮的齿数;
x1、x2——分别为外、内齿轮的径向变位系数。
可得:在z1、z2和α一定时,变位系数xl和x2的变化直接影响到啮合角α′的大小,啮合角是变位系数的函数;而选择变位系数xl、x2的问题,实质上是决定内啮合齿轮副是否能够消除干涉现象。对于一对啮合齿轮,可把变位系数视为自变量,而把其余的参数作为常量,即限制条件是变位系数的函数。因此,满足两个主要限制条件的问题便归结为求合适的变位系数的问题。
某项限制条件,可以曲线的形式表示在xl,x2坐标系内,若把每个限制条件都以曲线形式绘于x1,x2坐标系内,则它们的交点A便对应着这对齿轮的变位系数,如图4-2所示。
由于限制条件中有许多是超越方程,直接求解变位系数非常困难或是不能求解。因此,本文将讨论如何用逐步逼近的迭代方法来求得同时满足两个主要限制条件的变位系数x1和x2。

少齿差内啮合的重合度计算公式为:

把变位系数x1,x2取作独立变量,把啮合角α′取作中间变量,用牛顿法求解。其迭代程序为:

其中εα′,GS′分别为设计要求的少齿差内啮合的重合度和齿廓不重迭干涉系数。
应用上述公式迭代时,参考机械工程手册,只要初始值(x1(0),x2(0))选得接近精确解(x1,x2),迭代过程就会收敛。
外齿轮的齿顶圆半径:

式中 z0,x0——插齿刀的齿数、变位系数;
da0——插齿刀z0的齿顶圆直径,da0=m(z0+2ha0*+2x0);
ha0*——插齿刀的齿顶高系数与顶隙系数之和;
a02′——插齿刀加工内齿轮时的啮合角。
内齿轮与插齿刀的无侧隙啮合方程为:

借助于Mathenatica软件,推导出行列式元素为:
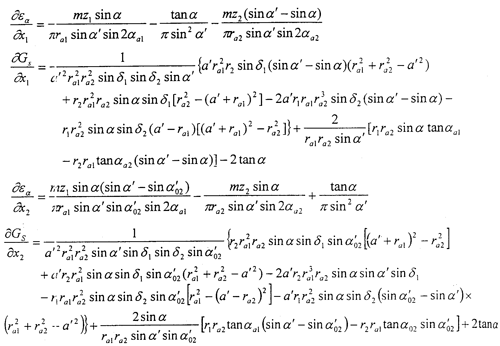
按照迭代过程求得的x1,x2是否满足设计要求,尚需检验变位外齿轮的齿顶厚系数,验算如下:
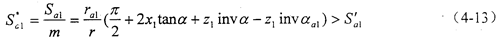
式中 Sa1′——设计要求的最小的外齿轮的齿顶厚系数。
根据上述公式推导,编制了迭代计算程序,程序框图如图4-3所示。
对于本文的实验样机HITSH145,内啮合齿轮副的参数为:z1=42,z2=44,m=3.5,ha*=0.8,ha0*=1.1,c*=0.3,α=20°,z0=22,x0=0.126,则可应用上述迭代公式求得当取εα′≈1.05及 GS′≈0.05时的外、内齿轮变位系数x1和x2。
按照文献中所述的内、外齿轮都按滚齿刀计算的迭代公式,最后得到的计算结果如下所示:
x1=1.433 x2=1.722
α′=38.192° εα=1.05
GS=0.05 c=1.377mm
a=4.185mm
并且验算外齿轮齿顶厚系数得:
Sa1*=0.546
给定初值x1=1.0、x2=1.5,迭代过程及迭代结果如表4-1所示。
按照本文所述的内齿轮为插齿、外齿轮为滚齿的加工方法的迭代公式,最后得到计算结果如下所示:
x1=1.142 x2=1.407
α′=37.356° εα=1.05
GS=0.05 c=c*m=1.05mm
a′=4.138mm
并且验算外齿轮齿顶厚系数得:
Sa1*=0.874

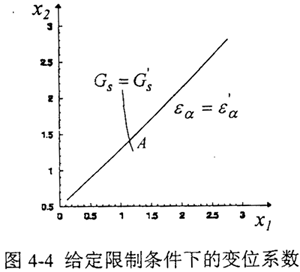
给定初值x1=1.0、x2=2.0,迭代过程及迭代结果如表4-2所示,给定限制条件下的变位系数选择如图4-4所示,交点A便对应着这对齿轮的变位系数x1=1.14204,x2=1.40742。
表4-1 按滚齿刀计算的迭代过程及迭代结果
| 迭代次数 |
第一次 |
第二次 |
第三次 |
第四次 |
第五次 |
| 变量 |
x1 |
1.64556 |
1.43467 |
1.43340 |
1.43339 |
1.43339 |
| x2 |
1.89802 |
1.72276 |
1.72248 |
1.72247 |
1.72247 |
| 迭代结果 |
εa |
0.999404 |
1.037740 |
1.050295 |
1.05 |
1.05 |
| GS |
0.610248 |
-0.050981 |
0.046851 |
0.049992 |
0.05 |
| c |
1.731905mm |
1.320847mm |
1.375545mm |
1.377092mm |
1.377092mm |
| α′ |
43.94741° |
36.89975° |
38.15867° |
38.19207° |
38.19207° |
| Sa1* |
1.218750 |
0.282717 |
0.544335 |
0.545879 |
0.545892 |
表4-2 滚齿刀计算的迭代过程及迭代结果
| 迭代次数 |
第一次 |
第二次 |
第三次 |
第四次 |
第五次 |
第六次 |
| 变量 |
x1 |
1.11301 |
1.14312 |
1.14215 |
1.14205 |
1.14204 |
1.14204 |
| x2 |
1.33214 |
1.40130 |
1.40740 |
1.40740 |
1.40742 |
1.40742 |
| 迭代结果 |
εa |
1.06348 |
1.06606 |
1.05024 |
1.05000 |
1.05000 |
1.05 |
| GS |
1.45340 |
-0.08768 |
-0.03195 |
0.04880 |
0.04993 |
0.05 |
| c |
1.05mm |
1.05mm |
1.05mm |
1.05mm |
1.05m |
1.05mm |
| α′ |
52.2256° |
35.6077° |
37.1097° |
37.3521° |
37.3685° |
37.3562° |
| Sa1* |
0.72848 |
0.878514 |
0.87514 |
0.87430 |
0.87424 |
0.87423 |
4.2.3 内齿环板的应力分析
内齿环板是三环减速机的关键传动零件,在该传动机构中实质是一连杆,承受一定的冲击;它又是一内齿轮,是一计算分析比较复杂的零件。其强度性能直接影响整机的运动和动态性能,因此有必要对内齿环板的应力和变形进行数值计算。对内齿环板进行有限元分析,首先应该对三环减速机在传动过程中的受力状况进行分析,建立曲型工况下的内齿环板的有限元计算模型;然后利用I-DEAS求出各模型的应力、变形分布及变化规律,对内齿环板强度状况进行研究。
本文研究的HITSH145型三环减速机的内齿环板的结构和受力情况如图4-5所示,该减速机的主要参数如表4-3所示。Ai孔轴、Bi孔轴为光孔输入轴,O孔为内齿轮,O孔轴为输出轴。每个内齿环板都受到三个力作用:Ai孔与配合轴间的作用力FAi、Bi孔与配合轴间的作用力FBi和O孔处的内齿轮与输出轴上的外齿轮之间的啮合力Fni。
表4-3 内齿环板主要参数表
| 输入转速n2 |
输出扭矩T |
齿数Z2 |
内齿轮模数m |
传动比i |
齿形角α |
压力角α′ |
| 966r/min |
875N·m |
44 |
3.5mm |
21 |
20° |
37.356° |
三环减速机的运动和动力通过两根相互平行且各带有三个偏心套的输入轴传递给三片内齿环板,三片环板上的内齿轮同时与输出轴上的外齿轮相啮合,啮合点间的相位差为180°,把运动和动力传递给输出轴。为了考虑三环减速机的惯性力和惯性力偶矩平衡,中间环板的厚度取为两侧环板厚度的两倍。假定两侧环板传递总功率的四分之一,则
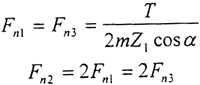
根据第二章的三环减速机的受力分析部分和内齿环板的有限元分析要求,可得内齿环板载荷工况如表4-4的上半部所示。在图4-5中,φ为Fni力作用点与x轴正向的夹角,φA、φB分别为FAi、FBi与x轴正向的夹角。表4-4的下半部列出的是φ在12个典型位置时的Fni、FAi、FB。
根据内齿环板轴向不能窜动及Ai、Bi孔圆周对称的特点,将约束处理为:圆周Ai、Bi的周边沿轴向(z向)单侧位移为零,同侧周边上、下、左、右极限位置处x、y方向位移为零,内齿轮O无约束。
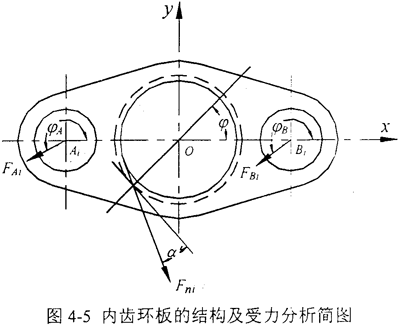
表4-4 内齿环板载荷工况表
| 载荷工况编号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
集中
力位
置角
(°) |
内齿轮φ |
0 |
30 |
60 |
90 |
120 |
150 |
180 |
210 |
240 |
270 |
300 |
330 |
| 左孔φA |
67.0 |
86.8 |
106.5 |
126.7 |
148.4 |
173.4 |
207.1 |
259.8 |
318.3 |
356.9 |
23.0 |
46.4 |
| 右孔φB |
29.1 |
80.2 |
136.4 |
175.1 |
202.7 |
225.6 |
246.6 |
226.7 |
286.8 |
307.4 |
329.5 |
355.1 |
集
中
力
F
(N) |
内齿轮O |
Fmx |
-2403 |
-2998 |
-2790 |
-1834 |
-387 |
1164 |
2403 |
2998 |
2790 |
1834 |
387 |
-1164 |
| Fmv |
-1834 |
-387 |
1164 |
2403 |
2998 |
2790 |
1834 |
387 |
-1164 |
-2403 |
-2998 |
-2790 |
| 左孔Ai |
FAi |
2145 |
2236 |
2190 |
2010 |
1714 |
1335 |
941 |
697 |
832 |
1203 |
1597 |
1925 |
| 右孔Bi |
FBi |
959 |
735 |
858 |
1206 |
1582 |
1897 |
2110 |
2198 |
2153 |
1980 |
1694 |
1331 |
根据三环减速机内齿环板的实际结构,设置单元类型、大小及材料特性,内齿环板的分析属于空间问题,选取四面体单元进行计算,选取单元长度为3mm,由Meshing模块共生成实体线性的四面体单元11658个,节点12170个,内齿环板的有限元网格如图4-6所示。12种载荷工况下各模型的约束处理都是相同的,由此建立了内齿环板在12个典型啮合位置时的有限元分析模型。建立约束集和解集,利用I-DEAS软件Model Solution模块对建立的12个有限元模型分别求解,可求出12种载荷工况下各模型的位移及应力如表4-5所示。12种载荷工况下内齿环板的最大位移如图4-7所示,12种载荷工况下内齿环板的最大应力如图4-8所示。
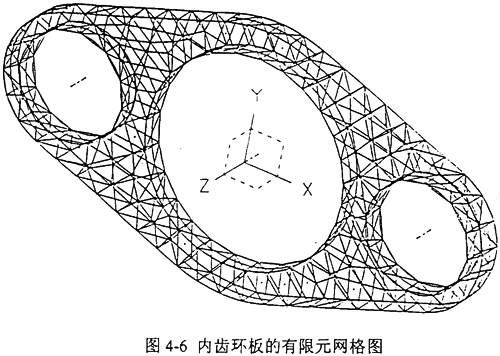
表4-5 内齿环板12种典型工况下的位移及应力计算结果
| 模型编号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
位移δ
10-3mm |
全局值 |
Max |
16.4 |
2.83 |
3.47 |
7.64 |
7.75 |
2.37 |
1.74 |
2.81 |
3.34 |
8.19 |
7.73 |
2.57 |
应力值
σMPa |
Max |
13.5 |
9.36 |
14.8 |
12.3 |
13.9 |
9.97 |
15.0 |
10.0 |
11.3 |
13.1 |
13.5 |
10.5 |
| Min×10-2 |
1.09 |
1.81 |
2.61 |
1.76 |
1.79 |
2.32 |
6.72 |
1.44 |
3.27 |
1.88 |
3.68 |
1.33 |
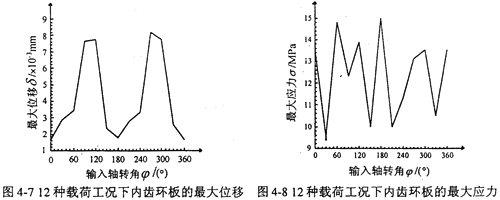
由图4-7、4-8可知,内齿环板的应力与位移都以360°为周期变化,最大位移出现在φ=270°时的工况位置,这是因为此时的啮合力Fni和Bi孔与配合轴间的作用力FBi都出现在φ=270°附近,它们的弯曲效应和剪切效应共同作用,出现位移的最大值点,同时也说明环板的最上部、最下部是环板位移的瓶颈环节;最大应力出现在180°+α′时的工况位置,这是因为此时的啮合力Fni、Ai孔与配合轴间的作用力FAi和Bi孔与配合轴间的作用力FBi都出现在φ=180°附近,它们的弯曲效应和剪切效应共同作用,出现应力的最大值点,同时也说明环板内齿轮与两个Ai孔、Bi孔的联接部分是内齿环板应力的瓶颈环节。
4.2.4偏心套的有限元分析
在三环减速机中,高速输入轴上要加工三对偏心轴颈,依次安装三个环板。由于中间一块环板的安装比较困难,一般采用图4-9所示的偏心套结构,高速轴1与偏心套2、3、4之间通过平键联接,轴与偏心套之间为过渡配合H7/k6,而偏心套通过环板轴承5与环板相联。
偏心套是高速输入轴上的主要传递扭矩部件,由第二章分析可得,偏心距e=4.18mm,由于偏心结构和装配位置上的限制,所以它成了三环减速机中的薄弱环节,有必要对其进行深入的分析。
对于偏心套来说,首先计算它的受力情况;假定中间环板的偏心套所受载荷为两侧环板的2倍,其它环板平均分配载荷。在额定输出扭矩T2=875N.m下,偏心套承受的扭矩为:
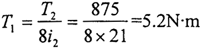
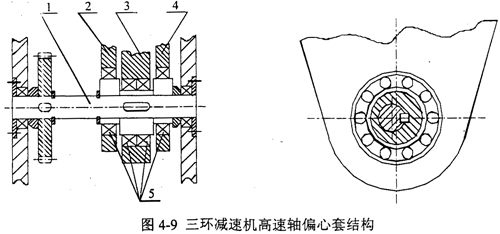
应用I-DEAS软件,按照空间问题求解,根据如图4-10所示的偏心套的结构,设置单元类型为四面体、单元长度为3mm及材料特性为45号钢,由Meshing模块共生成四面体单元3988个,节点1042个,它的有限元分析模型如图4-11所示,由于是平键联接,所以载荷均匀地作用在偏心套主动键槽一侧;由于偏心套可以转动。则边界条件取为偏心套内、外两个圆柱面z向旋转自由。建立约束集和解集,运用Model Solution模块求得结果如下:
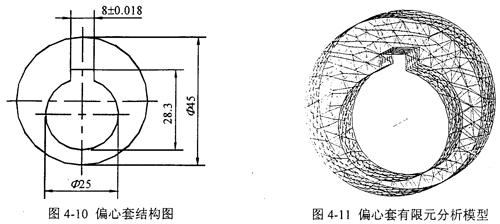
此时偏心套的位移ε为:
εmin=0;
εmax=l.43E-02mm,发生在键槽主动侧边。
此时偏心套的应力σ为:
σmin=2.38E-02MPa;
σmax=5.13E+01MPa,发生在键槽主动侧边。
偏心套的材料为45号钢,由机械工程手册第一卷查得:45号钢的抗拉强度σb≥3.35E+02MPa,远远大于σmax,所以足够满足强度要求,所以偏心套在工作状况下是安全的。
上一页
下一页