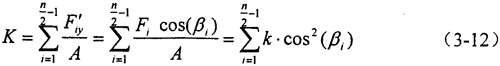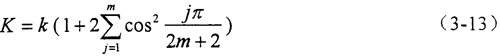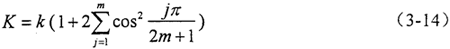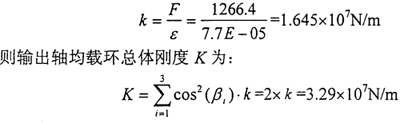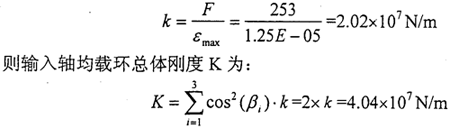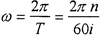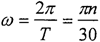3.5弹性均载环静力学分析
3.5.1弹性均载环的约束及载荷
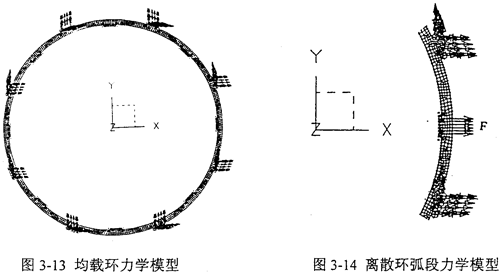
合理地确定弹性均载环的约束及载荷,是正确进行弹性均载环静力学和动力学分析的关键。由于均载环置于输入轴和输出轴的轴承外圈和轴承座孔之间,轴承座和箱体是一体,箱体固定在工作台上,所以边界条件取为均载环的八个外凸台固支,作用力F作用在内凸台表面上。均载环的力学模型如图3-13所示。弹性均载环的内外表面分别均匀分布八个凸台。为了便于有限元分析,可以将均载环离散成八个环弧段,每个环弧段由一个内凸台和其相临两个外凸台之间的部分构成,内凸台受径向载荷,离散环弧段与均载环的载荷和边界条件相同。离散环弧段力学模型如图3-14所示。
3.5.2用弹性力学的方法求解均载环的刚度
弹性力学是固体力学的一个分枝,主要研究物体(弹性体)由于受外力作用或温度改变以及支座沉陷等原因而产生的应力、形变和位移,弹性力学对弹性体作较精确的分析。对于本文的离散均载环弧段,环弧段的厚度h<<它的长度2L(或宽度2B),且挠度较小,可以利用弹性力学中薄板的小挠度变曲理论,将均载环结构参数与刚度联系起来,通过正确处理边界条件来改善计算结果。离散环弧段的计算模型如图3-15所示,假定环弧段的支承边界条件为两端固支。
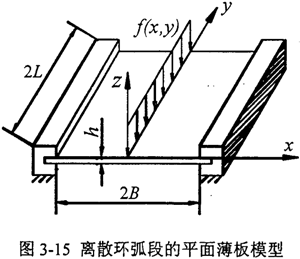
图中f(x,y)=F·δ(x)/2L为环弧段单位面积上的分布力。
式中 F——环板内凸台受力;
δ(x)=Dirac——力分布函数。
按照平面薄板的小挠度弯曲理论,薄板变形的控制方程为:
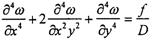
式中 D=Eh2/((12(1-μ2))为薄板的抗弯刚度;
h——薄板厚度;
μ——薄板材料的泊松比;
E——薄板材料的弹性模量。
边界条件取为:

上式为两端固支的环弧段刚度的计算公式,如将支承边界条件改为一端简支和一端固支或两端简支,则相应的环弧段刚度为两端固支刚度75%或50%。由式(3-8)可知,弹性均载环的厚度对其刚度的影响最大;在弹性均载环平均直径一定时,凸台尺寸及承载宽度对其刚度有一定影响。
由上述的输入轴均载环的实际结构参数,可以求出输入轴均载环环弧段的刚度为:
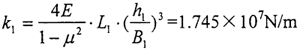
由上述的输出轴均载环的实际结构参数,可以求出输出轴均载环环弧段的刚度为:
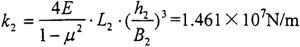
3.5.3用有限元方法求解均载环的刚度
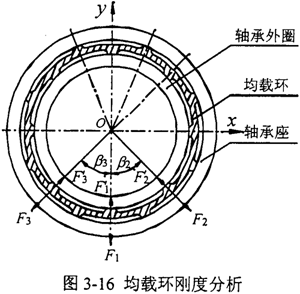
由3.5.1可知,将均载环离散成八个环弧段,每个环弧段由一个内凸台和其相临两个外凸台之间的部分构成,均载环刚度与其离散环弧段刚度之间的关系如图3-16所示。
弹性均载环的刚度定义:均载环中心所作用之力与环的中心在该力方向上位移之比。对于4m+4型、内外表面均匀分布n个凸台的均载环,若轴心沿-y方向有径向位移A,则轴承外圈受到均载环下半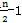 个内凸台的支反力Fi′(i=1,2,……,
个内凸台的支反力Fi′(i=1,2,……,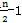 )作用,将均载环视为以外凸台中线为界的n个环弧段的组合,则均载环相应下半
)作用,将均载环视为以外凸台中线为界的n个环弧段的组合,则均载环相应下半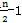 个环弧段内凸台的径向变形为:
个环弧段内凸台的径向变形为:
Ai=A·cos(βi) (3-10)
式中 βi——各弧段方位角,i=1,2,……,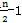 。
。
一般来说,由均载环结构的对称性可知其各离散环弧段具有相同的刚度k,于是各离散环弧段的支反力为:
Fi′=k·Ai=k·A·cos(βi) (3-11)
式中 k——环弧段刚度,单位为N/m,i=1,2,……,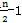 。
。
由均载环刚度定义,均载环总体刚度为:
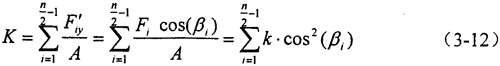
式中Fiy′——Fi沿y方向的分力,i=2,……,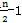 。
。
所以,对于n=4m+4类型的弹性均载环,总体刚度K与环弧段刚度k之间的关系可用下式表示:
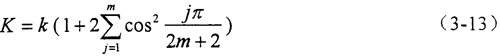
对于n=4m+2类型的弹性均载环,它具有双向刚度异性,总体刚度K与环弧段刚度k之间的关系可用下式表示:
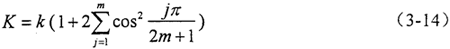
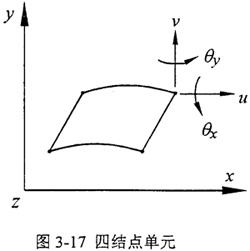
由上述分析可知:均载环离散成八个对称的环弧段,因此均载环总体刚度的计算归结为求解其离散的环弧段的刚度。本章利用I-DEAS分析软件计算内、外表面各均匀分布八个凸台的输入、输出轴弹性均载环的离散环弧段的刚度,从而得到均载环的总体刚度。对于图3-15所示的离散环弧段,内凸台的受力沿+x方向,并且在沿轴向方向上均匀分布,所以只需考虑xy平面内的形变分量和位移分量即可,可以认为是平面应力问题。在单元选择上,选用“平面应力问题”中的四结点单元,定义单元的四结点厚度与弹性均载环的宽度相一致。四结点单元如图3-17所示。
对于输出轴均载环,为了补偿前述的等效中心误差ymax,在实际分析时,当图3-15所示的离散环弧段的最大位移形变ε=ymax=0.077mm时,选用平面应力问题求解,根据均载环的实际结构,设置单元类型、大小及材料特性,选取四边形单元,单元长度选为0.4mm,对于输出轴均载环,由Meshing模块生成四边形单元3499个,节点4495个;均载环八个外凸台固支,建立约束集和解集,则可运用I-DEAS分析软件Model Solution模块计算得到环弧段内凸台受力F=1266.4N,力F均匀地分布在内凸台表面上。
此时离散环弧段的应力σ为:
σmin=6.49E-13MPa
σmax=3.74E+02MPa
由于均载环离散为八个对称环弧段,故整个输出轴均载环的最大应力就等于离散环弧段的σmax。均载环的材料为55Si2Mn,由机械工程手册查得:它的抗拉强度σb≥1.274E+03MPa,远远大于σmax,所以足够满足强度要求。
并且可以求出离散环弧段的刚度k:
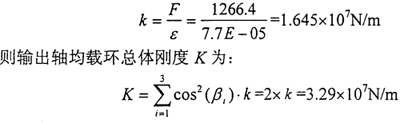
对于输入轴均载环,它的受力来源于一级传动的载荷分配不均匀力。由一级传动齿轮受力分析可知,假定一级传动载荷分配不均匀系数KP=1.50,则可得载荷分配不均匀力F=253N,力F均匀地分布在内凸台表面上。选用平面应力问题求解,根据均载环的实际结构,设置单元类型、大小及材料特性,选取四边形单元,单元长度选为0.4mm,对于输入轴均载环,由Meshing模块生成四边形单元1954个,节点2394个;均载环八个外凸台固支,建立约束集和解集,则可运用I-DEAS分析软件Model Solution模块计算得到环弧段的位移为:
εmin=0
εmax=1.25E-O2mm
此时离散环弧段的应力σ为:
σmin=8.43E-O2MPa
σmax=1.4IE+O2Mpa
由于均载环离散为八个对称环弧段,故整个输入轴均载环的最大应力就等于离散环弧段的σmax。均载环的材料为55Si2Mn,由机械工程手册查得:它的抗拉强度σb≥1.274E+03MPa,远远大于σmax,所以足够满足强度要求。
并且可以求出离散环弧段的刚度k:
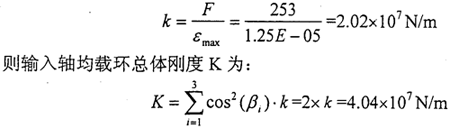
用平面薄板的小挠度理论计算得到的环弧段的刚度比用I-DEAS软件计算得到的环弧段的刚度要小约13.6%,因此在精度要求允许的情况下,可以用理论计算预估均载环的刚度,用来指导设计。
3.6弹性均载环动力学分析
机器中的传动部分是机器的基本组成部分,机械传动系统的优劣直接影响着机器性能的发挥。随着机械传动速度的提高,机械振动和平衡问题已经成为某些机械设计中的关键问题。各种机械在工作过程中所产生的振动,可使它们的动态性能严重恶化,从而降低其传动精度、生产效率、机械零件的寿命,甚至引起机械零件的破坏。同时,由于机械振动所产生的噪音,又可污染生产环境,影响人们健康。因此,动力学分析已经成为机械设计的必要手段。
动力学分析是指在已知系统的动力学模型(数学模型)、外部激振力和系统工作条件的基础上,分析研究系统的动力特性。动力学分析大致包括下列三方面的问题:
1.固有特性问题;
2.动力响应问题;
3.动力稳定性问题;
对于本文的均载环来说,作为减速机的一个子结构,它不可能产生自激振动。因此,在本章中只研究均载环的固有振动频率、模态振型和动力响应。求解多自由度有阻尼离散系统动力学问题,通常建立模型的运动方程,采用模态分析法和子空间迭代法,用高级语言编程求解系统受任意激振力作用下的固有频率和模态振型。在本章中,考虑到弹性均载环的运动方程难以建立,故而采用有限元方法来进行动力学分析。
3.6.1弹性均载环的固有特性
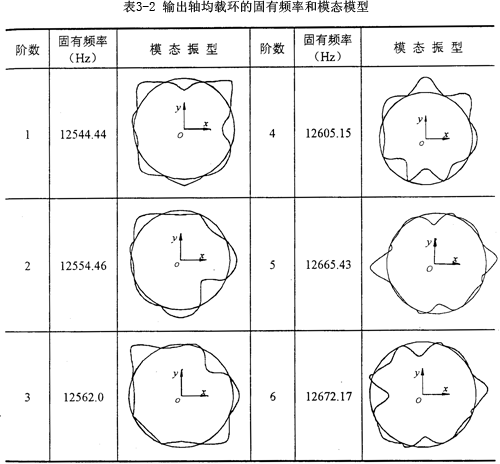
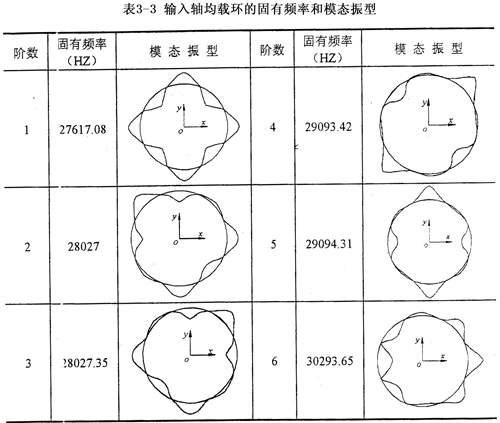
本文利用I-DEAS软件来进行弹性均载环的动力学分析。首先求解均载环的固有特性问题,在图3-14所示的均载环的力学模型中,均载环的边界条件取为均载环的八个外凸台固支,输出轴均载环和输入轴均载环的有限元模型参数同3.5.3,中研究的一致。应用Model草药Solution模块中的Model response部分,选用Normal Mode Dynalnics-SVI(普通模态动力分析——同步矢量迭代法)方法求得输出轴均载环和输入轴均载环的前六阶固有频率和模态振型分别如表3-2、3-3所示。
由表3-2可知,输出轴均载环的前六阶固有频率在1250OHz~12700Hz之间,这些固有频率远远高于三环减速机的转动频率和啮合频率,三环减速机几乎没有发生共振的可能性。由振动理论可知,构件的约束增多,尤其是固定约束增多,则它的固有频率将增大。本文中的输出轴均载环由于固定约束点较多而导致它的固有频率较高。
由表3-3可知,输入轴均载环的前六阶固有频率在2750OHz~30300Hz之间,这些固有频率远远高于三环减速机的转动频率和啮合频率,三环减速机几乎没有发生共振的可能性。本文中的输入轴均载环由于固定约束点较多而导致它的固有频率较高。
3.6.2弹性均载环的动力响应
首先求解输出轴均载环的动力响应问题,输出轴均载环的外部激振力来源于少齿差内啮合的载荷分配不均匀力F,由前述分析可知,考虑三环减速机主要制造安装误差,当离散环弧段的最大位移形变ε=ymax=0.077mm时,则可运用I-DEAS分析软件Model Sofution模块计算得到离散环弧段的内凸台受力F=1266.4N。力F均匀地分布在内凸台表面上。
载荷分配不均匀力F来源于三环减速机少齿差传动中的啮合力,啮合力的方向总是相切于齿轮的基圆,指向啮合点,在啮合的过程中,啮合力的方向总在周期地变化着。于是可得:在某一时刻具有n个内、外凸台的输出轴弹性均载环内凸台所受的载荷为:
Fi=F·cos(βi)
式中 βi为各内凸台与F力作用点之间的夹角,i=1,2,……,n;
通过对啮合力的分析,认为输出轴均载环受到简谐激振力Fcos(ωt)是合理的,其中ω为输出轴的回转角速度。根据传动关系可得:
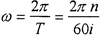
式中 T——输出轴回转周期;
n——输入电机转速。
取输出轴均载环的八个均布内凸台的中间点作为振动响应点,示意图如图3-18所示。取输出轴均载环系统粘性阻尼系数c=0.03,均载环的边界条件取为均载环的八个外凸台固支,输出轴均载环和输入轴均载环的有限元模型参数同3.5.3中研究的一致。于是应用I-DEAS分析软件Model Solution模块中的Model Response部分,可以求得弹性均载环的暂态激励幅频、相频响应特性曲线如图3-19。
同时可以救是输出轴均载环的动态挠度和动态主应力的最大值分别为:
ydmax=7.91E-05mm<[yd]
σdmax=1.43E-01MPa<[σd]
式中 [yd]——输出轴均载环许用动态挠度,本章中取[yd]=0.4mm;
[σd]——输出轴均载环许用动态主应力,本章中取[σd]=700MPa。
所以说:输出轴均载环的动态特性良好。
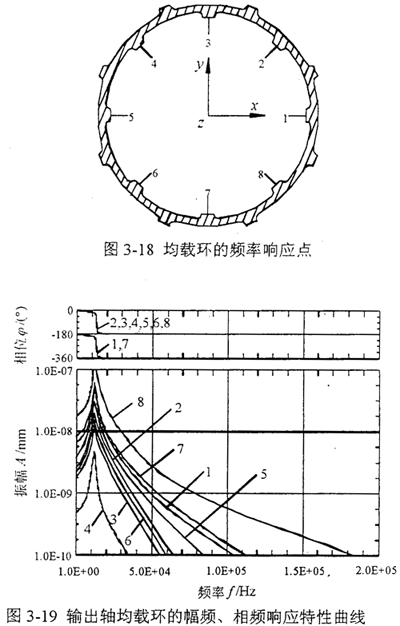
其次求解输入轴均载环的动力响应问题,输入轴均载环的外部激振力来源于定轴传动的载荷分配不均匀力F,由一级传动齿轮受力分析可知,假定一级传动载荷分配不均匀系数KP=1.50,则可得三环减速机的载荷分配不均匀力F=253N。
载荷分配不均匀国F来源于三环减速机定轴传动中的啮合力,啮合力的方向总是相切于齿轮的基圆,指向啮合点,在啮合的过程中,啮合力的波动总在周期地变化着。于是可得:在某一时刻具有n个内、外凸台的输入轴均载环内凸台所受的载荷为:
Fi=F·cos(βi)
式中 βi为各内凸台方位角,i=1,2,…,n。
通过对啮合力的分析,认为输入轴均载环受到简谐激振力Fcos(ωt)是合理的,其中ω为输入轴的回转角速度。根据传动关系可得:
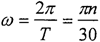
式中 T——输入轴回转周期;
n——输入电机转速。
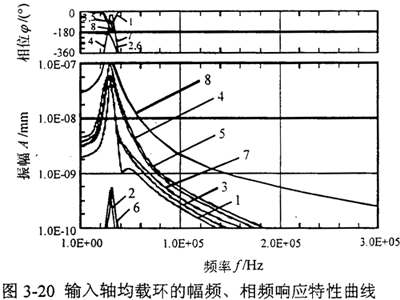
取输入轴均载环的八个内凸台的中间点作为振动响应点,示意图同图3-18所示。取输入轴均载环系统粘性阻尼系数c=0.03,均载环的边界条件取为均载环的八个外凸台固支,输出轴均载环和输入轴均载环的有限元模型参数同3.5.3中研究的一致。于是应用I-DEAS分析软件Model Solution模块中的Model Response部分,可以求得输入轴均载环的暂态激励幅频、相频响应特性曲线如图3-20所示。
同时可以求得输入轴均载环的动态挠度和动态主应力的最大值分别为:
ydmax=1.42E-10mm<[yd]
σdmax=1.81E+00MPz<[σd]
式中 [yd]——输入轴均载环许用动态挠度,本章中取[yd]=0.04mm;
[σd]——输入轴均载环许用动态应力,本章中取[σd]≥700MPa。
所以说:输入轴均载的动态特性良好。
3.7本章小结
本章在对三环减速机的制造安装误差和载荷分配进行深入分析的基础上,结合行星传动均载的原理,提出了一种新型的利用零件弹性变形均载的三环减速机均载机构一金属弹性环均载机构,并且对其进行静力学和动力学分析,从理论上验证均载环的均载效果。
衡量三环减速机载荷分配性能的指标是载荷分配不均匀系数KP,本章提出了一种利用非线性有限元方法一间隙单元法计算三环减速机载荷分配不均匀系数KP的方法,并对两种三环减速机进行了实例计算。载荷分配不均匀系数KP的确定不仅为三环减速机的载荷分配提供理论依据,而且为三环减速机均载机构的设计提供评价依据。
对弹性均载环进行静力学分析,用弹性力学平面薄板的小挠度分析理论和有限元分析的方法分别计算输入轴均载环和输出轴均载环的刚度和强度。
对弹性均载环进行动力学分析,利用I-DEAS分析软件对三环减速机的输入钟均载环和输出轴均载环进行了动力学分析,得到其前六阶固有频率、模态振型和瞬态激励频率响应特性曲线。
综上所述,金属弹性均载环具有较好的位移均载效果,能够满足位移均载要求,是一种理想的三环减速机均载机构。
上一页
下一页



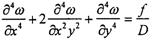

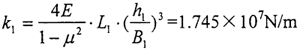
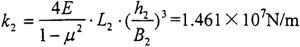
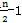 个内凸台的支反力Fi′(i=1,2,……,
个内凸台的支反力Fi′(i=1,2,……,