第2章 滚柱活齿传动啮合特性及润滑性能
2.1 引言
滚柱活齿传动由于同时具有径向尺寸小、承载能力高、结构紧凑、传动效率高等优点,因此在石油钻采及管道工程中具有广阔的应用前景。但目前对它的理论研究还很不完善,使得人们对它的设计还只能建立在经验和预估的基础上,所以对其进行理论研究对于深刻理解和更好地应用滚柱活齿传动具有重要意义。
本章将对滚柱活齿传动的啮合特性及润滑性能进行分析。首先根据相对运动关系,推导中心轮齿廓方程,并分析活齿中心运动轨迹曲率的特点,再根据弹性力学理论和变形协调条件建立其力学模型,最后分析润滑状态并求解油膜厚度,从而为设计、分析和加工滚柱活齿传动减速器奠定理论基础。
2.2 滚柱活齿传动原理及特点

滚柱活齿传动系统(见图2-la)主要由波发生器H、活齿G、活齿架S、中心轮R四个部分组成。如图2-lb所示,滚柱活齿传动系统在工作时,输入驱动力后,输入轴以等角速度ωH,逆时针旋转,从而带动波发生器使其几何中心O′绕旋转中心O以同样角速度旋转,波发生器半径变化的轮廓曲线产生径向推力,迫使与中心轮工作齿廓接触的诸活齿,在沿活齿架径向导槽移动的同时,沿着中心轮工作齿廓滑滚,并通过活齿架的径向导槽推动活齿架以匀速ωS逆时针转动,于是滚柱活齿传动完成了输入速度ωH、输出速度ωS的转速变换运动。而与中心轮非工作齿廓接触的诸滚柱活齿,在活齿架径向导槽推动下,顺序地返回到导槽内工作起始位置,从而分别完成了各自的运动循环。
由滚柱活齿传动的结构可知,滚柱活齿G是个三副件,它与中心轮R、波发生器H和活齿架S形成了三个高副,所以研究滚柱活齿传动啮合状态首先要研究一个啮合副在一个运动循环中的啮合过程。对于常用的波幅ZH=1的波发生器,其轮廓被经过几何中心O′和旋转中心O的连线分为两部分:升程曲线和回程曲线,它每转一周推动活齿径向往复一次,成为啮合副的一个运动循环。与升程曲线接触的活齿在波发生器的推动下,由中心轮的齿顶向齿根运动,而与回程曲线接触的活齿则由中心轮的齿根向齿顶运动。波发生器每转一周推动活齿径向往复一次,称为啮合副的一个运动循环。在一个运动循环中,活齿与中心轮轮齿接触点的轨迹形成了中心轮R的一个齿。由啮合副的啮合过程可知:与波发生器H的升程曲线接触的活齿都处于啮合状态,而与波发生器H的回程曲线及远停、近停曲线接触的活齿都处于非啮合状态,所以我们将波发生器H的升程曲线所对的圆心角称为工作区域角,工作区域角内为啮合区,而把它的回程曲线(包括远停、近停曲线)所对的圆心角称为非工作区域角,非工作区域角内为非啮合区。
2.3 中心轮齿廓方程的建立及齿廓仿真
根据滚柱活齿传动原理可知:中心轮齿廓曲线是活齿G在运动过程中齿廓曲线族的包络线。当活齿传动不发生顶切时,该包络线就是活齿中心运动轨迹的等距线。所以,欲求中心轮齿廓方程就要先求出活齿中心运动轨迹的方程。
2.3.1 活齿中心运动轨迹方程的建立
滚柱活齿传动的连续性是靠彼此间存在相差的并联啮合副交替工作来实现的。因为各个并联的啮合副从啮合开始到结束的工作过程完全相同,相邻两个啮合副仅差一个相位,所以研究与相位无关的齿廓方程,可以任选一个活齿作为研究对象。另外,在工作时,需将中心轮R 或活齿架S 固定一个(常固定中心轮R )。
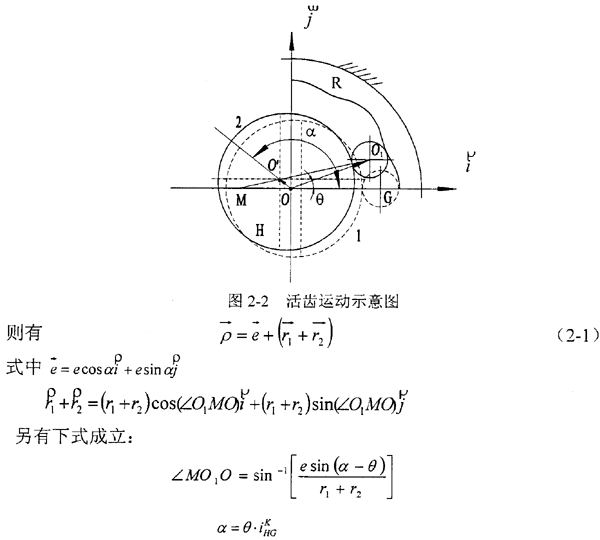
中心轮R 静止时,与之固连的坐标系为 (图2-2) ,波发生器H匀速逆时针旋转,设活齿在波发生器上作纯滚动并在中心轮齿廓限制下推动活齿架作匀速逆时针转动。波发生器H 的几何中心为O′,活齿G 的几何中心为O1。在矢量ΔO O′O1中,矢量
(图2-2) ,波发生器H匀速逆时针旋转,设活齿在波发生器上作纯滚动并在中心轮齿廓限制下推动活齿架作匀速逆时针转动。波发生器H 的几何中心为O′,活齿G 的几何中心为O1。在矢量ΔO O′O1中,矢量 即为所求的活齿中心运动轨迹曲线的径矢,
即为所求的活齿中心运动轨迹曲线的径矢, 为波发生器半径矢量
为波发生器半径矢量 ,r2μ为活齿半径矢量(|r2μ|=r2),则
,r2μ为活齿半径矢量(|r2μ|=r2),则 。初始位置1时,
。初始位置1时, 、
、 和iμ轴重合,经过一段时间后,波发生器H 和活齿G 转到位置2时,设
和iμ轴重合,经过一段时间后,波发生器H 和活齿G 转到位置2时,设 与iμ轴成α角,
与iμ轴成α角, 与iμ轴成θ角。
与iμ轴成θ角。
式中iHGK—中心轮R 固定时,波发生器输入、活齿架输出时的传动比。
同时为方便计算,令l=e/(r1+r),φ=∠MO1O,则∠O1MO=θ-φ,代入式(2-1)整理得活齿中心轨迹方程为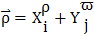 ,即:
,即:

2.3.2 中心轮齿廓方程的建立
在不发生顶切的情况下,中心轮齿廓曲线就是活齿中心运动轨迹的外等距线,表示为:
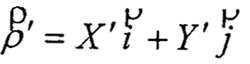
式中ρ'ρ——中心轮齿廓曲线的径失。
根据式(2-2),得活齿中心轮齿廓方程为:

2.3.3 中心轮齿廓仿真
为验证以上理论推导的正确性并直观地显示出活齿传动中的啮合情况,拟对其进行仿真研究。为显示齿廓的三维曲面,将齿廓曲面对应的自变量区域(XOY平面上)划分为5×34个网格。先由数学模型计算出中心轮和活齿齿面上对应自变量区域网格节点的值,得到齿廓曲面的网格图,然后采用二维线性插值的方法,得到整个齿廓曲面。同时,比较活齿与中心轮齿廓曲面上对应点的坐标值,将坐标值相同的点(接触点)在图象上以另一种颜色显示,以便观察接触的情况。编程采用具有很强矩阵处理功能和绘图功能的MatLab 语言。
活齿与波发生器的啮合情况见图2-3,可以清楚地看到接触线为一条直线。从生成的接触点的坐标可以看到,这些点的坐标中只有x值变化,而y和z 的坐标值相同,也就是这些点在空间上组成了一条平行于x轴的直线,说明活齿与波发生器之间不但是线接触,而且这条接触线也平行于活齿的回转轴。
采用相同算法得到活齿与中心轮啮合时齿廓曲面的三维图形(图2-4 ),同样可见其接触线也是一条平行于回转轴的直线。

2.4 活齿中心运动轨迹曲率的确定及其特点
在活齿传动的啮合理论分析中,常常要用到中心轮齿廓上任意一点的曲率K,而根据中心轮齿廓方程直接计算曲率极为复杂。
另一方面,由于波发生器的半径常常远大于活齿半径(通常十几倍),所以活齿中心运动轨迹曲线上任意一点的曲率仅比它的等距线——中心轮齿廓曲线上对应点的曲率略大,在接触疲劳强度计算中可以近似认为相等。这样不但使活齿的理论分析变得可行,同时也可大大地简化计算,使之更便于工程应用。另外,这样近似计算的结果使得到的接触疲劳强度略偏于安全,设计更为可靠。
活齿中心运动轨迹的曲率为:
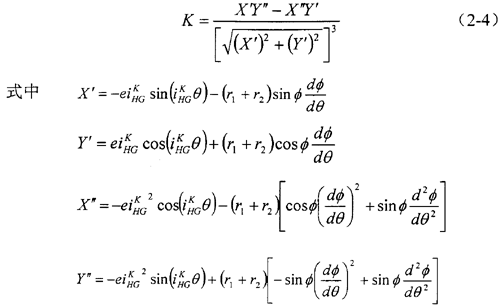
一滚柱活齿传动减速器,偏心距e =1.5mm,波发生器半径r1=30mm,活齿半径r2=8mm,传动比iHGK=9。采用MatLab编程,分别得到活齿中心运动轨迹和中心轮齿形(图2-5)以及活齿中心运动轨迹的曲率K与活齿架旋转过的角度θ之间的关系曲线(图2-6)。


推而广之,并考虑到中心轮齿廓曲率的变化趋势与活齿中心运动轨迹相同,可得到中心轮曲率K的特点如下:
(1)由图2-6中K-θ曲线可以看出,中心轮每一个齿在齿根处曲率最大,曲率半径最小。沿着齿廓上升的过程中曲率减小到零后,继续减小为负值。到达齿顶时,曲率最小。
(2)齿顶处曲率的绝对值要小于齿根处的曲率绝对值。也就是说,齿根处的曲率半径要略小。所以在结构设计中可用齿根处的曲率半径来保证不发生顶切,在强度校核计算中可用齿根处的曲率半径来计算以使结果略偏于安全。
2.5 滚柱活齿传动力学模型的建立
2.5.1 单个活齿受力分析
波幅ZH=1 的滚柱活齿传动在理论上每一时刻都有半圈活齿参与啮合,属于复杂的过约束机构,无法用刚体力学完全确定,必须根据弹性力学理论和变形协调条件建立其力学模型。分析可知,不同活齿在每个运动循环中受力情况相同,不失一般性,从图2-la中右侧逆时针任取第j个活齿作研究对象。不计重力和摩擦力,活齿受力如图2-7 所示。
固定中心轮R,不失一般性,选择活齿数ZG与中心轮齿数ZR之差为1。此时传动比大小等于活齿个数。假设开始时,波发生器的几何中心O1在X轴上,该活齿中心在B点,波发生器以角速度ω逆时针转动。t时刻时,波发生器转过θ角,该活齿中心运动到Bl点,波发生器的几何中心从Ol运动到O2;Fsj、FHj、FKj分别为活齿架、波发生器、中心轮对该滚柱活齿的法向压力。
根据传动比的定义和波发生器与活齿间相对运动关系,得到:

式中iHGK——中心轮固定时,波发生器输入、活齿架输出时的传动比;
θ——波发生器逆时针转过的角度。

式中
kn—活齿中心运动轨迹在Bl点处的法线斜率;
ax—活齿中心在X方向的加速度;
ay—活齿中心在Y方向的加速度。
根据活齿中心运动轨迹方程:

其中dj=(r1+r2)sin∠OO2B1/sin∠B1OO2。每个活齿有3个未知数,共有3ZG个未知数,方程数为2ZG+l个,需要补充ZG-1个方程,方可求解。
考虑变形协调条件,设第j个活齿的接触变形量分别为δHj,δKj和δSj,导致活齿中心与旋转中心O的连线OB1转过微小角度θG,反映在坐标系中,就是活齿中心B在水平和垂直两方向微小的位移Bxj和Byj,可列:

式(2-7)和式(2-8)联立,其中未知数为θG、Bxj和Byj,共有2ZG+l个,而方程共有3ZG个,所以ZG-1为式(2-7)和式(2-8)联立后实际补充的方程数,它与式(2-5)和式(2-6)联立后需要补充的方程数相等,所以原方程可解。
2.5.2 双排结构滚柱活齿受力分析
在实际应用中,为平衡掉负载对支承的径向作用,一般采用180°对称布置的双排结构,两排活齿共用一个活齿架。图2-8 中O′a′、O″A″分别表示第一排、第二排波发生器的偏心距。在以下分析中约定:上角标“′”表示第一排活齿传动的参数,上角标“″”表示第二排活齿传动的参数。T1、T1′和T1″分别表示输入轴上的总输入力矩、第一和第二个波发生器分担的输入力矩。在输入力矩的作用下,输入轴和波发生器发生扭转变形使两波发生器的相位差由理论的180°有了一个相对的变化△φ,从而使两排活齿的受力情况略有不同,所承担的扭矩也不同。为此,引入载荷传递不均匀系数Kp,设第二排活齿传递的扭矩为KpT2,则第一排活齿传递扭矩为(l-KP)T2,其中T2为输出轴上输出的总扭矩。
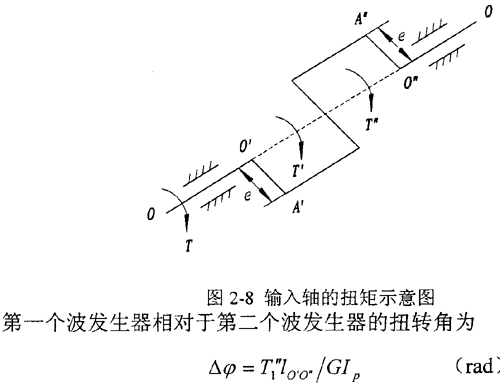
式中lO′O″—— 两波发生器轴向距离即O′O″距离;
G——材料的剪切弹性模量;
Ip——轴截面极惯性矩,πD4/32(mm4),D为轴直径;

由于输入轴的扭转变形,使第二个波发生器相对于第一个波发生器发生了△φ的转角,假设波发生器固定,由相对运动关系可知,相当于活齿架发生了△φ/iHGK的偏转角,又因在Tl″的作用下,活齿架发生了θG″的偏转角,故第二个活齿架的总偏转角为θG″+△φ/iHGK,同时在Tl′作用下活齿架的微转角为θG′,因两排活齿共用一个活齿架,故得

由公式(2-8),可用Bxj′、Byj′和θG′等2ZG+l个未知量代换式(2-10)中的FHj′、FKj′和FSj′等3ZG个未知量,从而将方程组化为含Bxj′、Byj′、θG′和KP等2ZG+2个未知量的2ZG+1 个方程的方程组。同理可将式(2-11)变换为含Bxj′、Byj′和θG′等2ZG+1个未知量的2ZG+l 个方程的方程组,联立式(2-9)、(2-10)、( 2-11) ,可得一个含4ZG+3个方程的方程组,而该方程组的未知量Bxj′、Byj′、θG′、Bxj″、Byj″、θG″及KP共有4ZG+3个,故完全可以求解。
2.5.3 计算实例
一特种用途的滚柱活齿减速器,采用双排结构,中心轮固定,波发生器输入,活齿架输出。输出扭矩为150Nm,输入轴转速n1=2980rpm,结构参数为:波发生器几何中心相对旋转中心的偏心距e=1.5,波发生器半径r1=30,活齿半径r2=8,活齿数ZG=9,中心轮齿数ZR=8,活齿架内径DS=66,外径DM=86,两排活齿轴向距离lO′O″=76,活齿长L=60,(长度单位:mm)。 活齿材料为GCr15,密度7.8×10-6kg/mm3,载荷不均匀系数kp=0.4953。根据公式(2-5)~(2-11),采用牛顿法求解联立方程组。为方便初值的确定,先用高斯法求解,将所得的解作为初始值,然后再用牛顿法求解方程组。采用MatLab编程计算,当OO1逆时针转过4°时,各力情况见表2-1。
表2-1 实例的计算结果
| 第一排活齿 |
第二排活齿 |
| 活齿 |
FH |
FK |
FS |
kp |
FH |
FK |
FS |
| 2 |
1.064 |
1.362 |
1.142 |
0.4953 |
1.027 |
1.393 |
1.297 |
| 3 |
1.002 |
1.176 |
1.120 |
0.993 |
1.133 |
1.099 |
| 4 |
0.883 |
0.971 |
0.983 |
0.871 |
0.983 |
0.896 |
| 5 |
0.781 |
0.826 |
0.651 |
0.779 |
1.120 |
0.912 |
注:因第一个活齿开始进入非工作齿廓,故不考虑它的受力情况。
2.6 滚柱活齿传动的润滑性能分析
减速器的润滑状态直接影响其摩擦和磨损的程度,进而对其寿命产生影响。为了准确把握和评价滚柱活齿减速器的润滑特性,本节拟对其进行分析,判断其润滑状态,求解油膜厚度。
2.6.1 润滑状态的判断及油膜厚度的计算
滚柱活齿减速器在工作时,活齿与活齿架、活齿与波发生器、活齿与中心轮之间皆为线接触高副,且减速器内充满润滑油,这时的各运动副之间的润滑属于既要考虑润滑油的粘压效应,又要考虑高副构件表面弹性变形的弹性流体动力润滑(EHL)。同时,由于高副间的相对运动要产生温升以及工作在采油井下,在分析时,必须要考虑润滑油及高副运动件之间的热平衡,也就是属于热弹流问题。所以,本润滑属于线接触稳态全膜热弹流润滑,润滑油按牛顿流体处理。先分析波发生器与活齿之间的润滑情况,活齿与中心轮、活齿与活齿架之间的情况完全类似,只是计算时几何参数略有不同。
根据计算流体动力润滑膜厚的张鹏顺统一公式,最小膜厚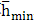 和中心膜厚
和中心膜厚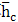 为:
为:

u——接触体表面的平均速度(卷吸速度)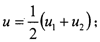 ;
;
w——单位接触线长度上的载荷。
山于活齿与中心轮、活齿架和波发生器之间存在高速滚动,而且在滚动的同时又伴有相当的滑动,所以热效应不能忽略。
引入热承载参数L,它反映润滑剂热特性和滚动速度的大小。
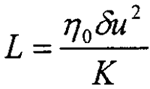
式中
δ——粘温系数;
K——润滑油导热率。
考虑热效应时的最小膜厚为Hin,对应的等温的膜厚为Hmin,ISO,则有:
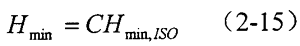
式中
C——考虑入口剪切热的修正因子, ;
;
z——滑滚比,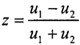 。
。
以上是针对波发生器和活齿之间的润滑情况分析,对于活齿和中心轮之间以及活齿和活齿架之间的情况完全相同,不同的是当量半径和卷吸速度的计算。
2.6.2计算实例
一滚柱活齿减速器,波发生器半径rl=30mm,偏心距e=1.5mm,活齿半径r2=8mm,传动i=9,波发生器转速n=2850rpm,材料的弹性模量E1=E1=2.1×1011N/m2,泊松比v1=v2=0.3,粘压系数α=2.2×10-8Pa-1,常压下润滑油的粘度粉η=35.8×10-3N·S/m,粘温系数δ=0.017。
由公式(2-12)~(2-15),编程计算得t=0.6316,根据润滑状态的判断条件,当5/9<t<1时,是弹性流体动力润滑状态,且常温时最小油膜厚度为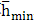 =0.8920μm,中心膜厚为
=0.8920μm,中心膜厚为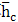 =1.0989μm。考虑热效应时的修正因子为C= 0.7148 ,最小油膜厚度为
=1.0989μm。考虑热效应时的修正因子为C= 0.7148 ,最小油膜厚度为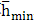 =0.6376μm。
=0.6376μm。
2.7 本章小结
1.根据滚柱活齿传动的相对运动关系,建立了活齿中心运动轨迹方程和中心轮齿廓方程,并仿真出齿廓曲面;给出了活齿中心运动轨迹曲线上任意一点曲率K 的计算方法,分析了中心轮在齿根和齿顶处曲率半径的特点。
2.在单个活齿受力分析的基础上,根据变形协调条件,给出了滚柱活齿的受力计算公式,为滚柱活齿传动的强度设计奠定了基础。
3.深入分析了滚柱活齿传动的润滑性能,给出了活齿与波发生器之间的油膜厚度的计算方法,确定了润滑状态是属于线接触稳态全膜热弹流润滑。
4.以一具体滚柱活齿减速器为例,得到了活齿中心运动轨迹上任意一点曲率K与活齿架旋转过的角度θ之间的关系曲线,求出了两排活齿的受力情况,计算出活齿与波发生器之间的油膜厚度。
上一页
下一页


 (图2-2) ,波发生器H匀速逆时针旋转,设活齿在波发生器上作纯滚动并在中心轮齿廓限制下推动活齿架作匀速逆时针转动。波发生器H 的几何中心为O′,活齿G 的几何中心为O1。在矢量ΔO O′O1中,矢量
(图2-2) ,波发生器H匀速逆时针旋转,设活齿在波发生器上作纯滚动并在中心轮齿廓限制下推动活齿架作匀速逆时针转动。波发生器H 的几何中心为O′,活齿G 的几何中心为O1。在矢量ΔO O′O1中,矢量 即为所求的活齿中心运动轨迹曲线的径矢,
即为所求的活齿中心运动轨迹曲线的径矢, 为波发生器半径矢量
为波发生器半径矢量 ,r2μ为活齿半径矢量(|r2μ|=r2),则
,r2μ为活齿半径矢量(|r2μ|=r2),则 。初始位置1时,
。初始位置1时, 、
、 和iμ轴重合,经过一段时间后,波发生器H 和活齿G 转到位置2时,设
和iμ轴重合,经过一段时间后,波发生器H 和活齿G 转到位置2时,设
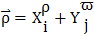 ,即:
,即:
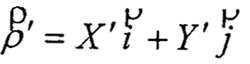


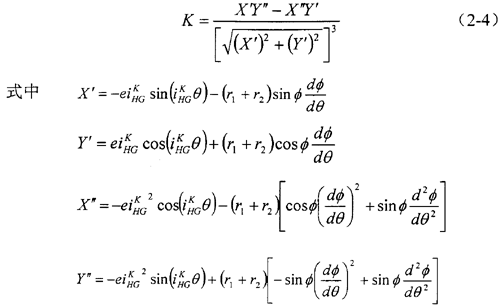









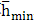 和中心膜厚
和中心膜厚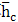 为:
为:
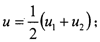 ;
;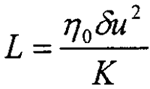
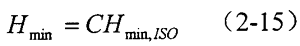
 ;
;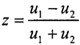 。
。