|
5.4.3计算实例
根据据第三章所设计的减速器及本章建立的故障树对减速器进行可靠性的计算机仿真研究。其各基本元件寿命分布参数见表5-2,采用上述算法编程求解。
通扫故障树2000次,产生减速器寿命抽样值2000个,设系统最大工作时间Tmax为1000h,考察减速器在工作8760h的可靠度。将Tmax分为1000个区间,统计减速器寿命抽样落入各区间的次数,得到减速器可靠度的仿真值与工作时间的关系曲线如图5-3所示。由式(5-13)~(5-20)求得减速器的其他可靠性指标如表5-3和表5-4所示。
表5-2基本元件失效分布类型及参数

注:基本元件17~22的分布参数与元件11~16的相同
根据图5-3和表5-3可知,减速器工作876Oh的可靠度为0.982,完全满足0.967的设计要求,仿真结果的绝对误差为0.467%。系统平均寿命,即减速器平均无故障工作时间MTBF为9874.9h。从表5-4可知,基本元件1~10的重要度W(Zi)值均为1.0,这与或门的逻辑关系相一致,说明这些部件具有相同的重要性。从模式重要度WN(Zi)可以看出,活齿架的模式重要度WN(Z16)和WN(Z22)远远大于其它元件,显然是系统的最薄弱环节,它的可靠性对减速器的寿命影响最大,所以提高活齿架的可靠性是改善滚柱活齿减速器可靠性的关键。
5.5 系统故障树的模糊化分析方法
由于现实环境中存在着大量“亦此亦彼”的模糊现象,而传统的故障树分析方法不能反映基本事件非稳态和各态历经的特点,为了使故障树分析的结果能更准确、更深刻地反映滚柱活齿减速器的可靠性问题,本节将模糊数学引入滚柱活齿减速器的可靠性分析中,采用模糊数的运算法则以及针对故障树各“门”的逻辑运算的模糊算子AND和OR求解系统可靠性的模糊数值。

表5-3减速器可靠性仿真结果
| 减速器可靠度 |
减速器平均寿命
(h) |
减速器寿命的方差
(h2) |
减速器不可靠度估值 |
仿真的误差估计 |
| 0.982 |
9.8749×103 |
8.1603×105 |
0.018 |
0.467% |
表5-4基本元件重要度和模式重要度
| 部件代号 |
W(Zi) |
WN(Zi) |
部件代号 |
W(Zi) |
WN(Zi) |
| 1 |
1.0 |
0.012 |
12 |
0.133 |
0.002 |
| 2 |
1.0 |
0.015 |
13 |
0.111 |
0.001 |
| 3 |
1.0 |
0.005 |
14 |
0.103 |
0.012 |
| 4 |
1.0 |
0.004 |
15 |
0.071 |
0.001 |
| 5 |
1.0 |
0.008 |
16 |
0.143 |
0.374 |
| 6 |
1.0 |
0.005 |
17 |
0.093 |
0.002 |
| 7 |
1.0 |
0.004 |
18 |
0.201 |
0.005 |
| 8 |
1.0 |
0.115 |
19 |
0.087 |
0.003 |
| 9 |
1.0 |
0.013 |
20 |
0.167 |
0.001 |
| 10 |
1.0 |
0.001 |
21 |
0.087 |
0.005 |
| 11 |
0.091 |
0.002 |
22 |
0.941 |
0.406 |
5.5.1模糊数的运算法则
采用模糊数来描述事件发生手概率,既能减少获取事件发生概率精确值的难度,同时双能结合工程中的实际经验和判断构造模数的隶属函数,较准确地把它们描述出来,并能在一定程度上容忍描棕的误差,因此该方法有较大的灵活性和适应性。
定义1模糊数为论域R上的连续模糊集,其凸隶属函数满足
maxμ(x)=1 x∈R
由定义1可知,模糊数的隶属函数可以有多种形式,其最大值不能超过1。
定义2若函数L满足
(1)L(x)=L(-x)
(2)L(0)=1
(3)L(x)在[0,∞]上非增且逐段连续
则称函数L为模糊数的参照函数。
定义3设L、R为模糊数的参照函数,则称模糊数为L-R型模糊数,若


线性型参照函数在“完全属于”和“完全不属于”之间的中介状态是线性变化的(见图5-3a),当x≤m-α和x≥m+β时,μ=0,说明在(m-α, m+β)区间之外的数值完全不属于该模数数,而其他类型的隶属函数曲线两端延伸到无穷远(图5-3b,c),说明整流器个数轴上的任何数总在一定程度上隶属于该模数数。在选择参照函数时,除非有绝对的扰握认为该事件发生的概率在某个范围之间而选择线性参照函数,否则,以选取正态型或尖型为好。

模糊数的代数运算法则如下:

式(5-25)、(5-26)是近似的,严格地说,两个L-R型模糊数相乘或相除,其结果不再是L-R型模糊数。
5.5.2模糊算子AND和OR
模糊算子AND和OR反映了“与门”和“或门”的模糊逻辑计算。对于“与门”,其模糊算子为;


5.5.3减速器的模糊故障树分析方法
在建立的滚柱活齿减速器故障树中,用模糊算子AND和OR描述其本事件之间的逻辑关系。生成真值函数的模糊形式及采用模糊算子表达的形式见表5-4。根据模糊数据的运算法则式(5-25)、(5-26)和模糊算子AND和OR的计算方法式(5-28)、(5-30)即可确定顶事件发生的模糊概率。

5.5.4计算和分析实例
以第三章设计的减速器为例,采用上述方法进行具体计算。假定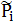 的参照函数为正态对称型且与均值mi相差±50%的点x的隶属度为0.1,则其中各基本事件故障概率的均值mi及计算得到的分布αi和βi如表5-5所示。 的参照函数为正态对称型且与均值mi相差±50%的点x的隶属度为0.1,则其中各基本事件故障概率的均值mi及计算得到的分布αi和βi如表5-5所示。

表5-5基本事件的均值mi用分布αi和βi
| 符号 |
基本事件 |
均值mi |
分布αi和βi |
符号 |
基本事件 |
均值mi |
分布αi和βi |
| X1 |
轴承1失效 |
1×10-4 |
3.29×10-5 |
X9 |
电源开关失效 |
1×10-4 |
3.29×10-5 |
| X2 |
轴承2失效 |
1×10-4 |
3.29×10-5 |
X10 |
系统保险丝烧断 |
5×10-4 |
1.65×10-4 |
| X3 |
轴承3失效 |
1×10-4 |
3.29×10-5 |
X11 |
活齿磨损失效 |
2×10-4 |
6.59×10-5 |
| X4 |
轴承4失效 |
1×10-4 |
3.29×10-5 |
X12 |
波发生器磨损失效 |
2×10-4 |
6.59×10-5 |
| X5 |
轴承5失效 |
1×10-4 |
3.29×10-5 |
X13 |
活齿磨损失效 |
2×10-4 |
6.59×10-5 |
| X6 |
轴Ⅰ断裂 |
2×10-5 |
6.59×10-5 |
X14 |
中心轮磨损失效 |
2×10-4 |
6.59×10-5 |
| X7 |
轴Ⅱ断裂 |
2×10-5 |
6.59×10-5 |
X15 |
活齿磨损失效 |
2×10-4 |
6.59×10-5 |
| X8 |
电源未开 |
1×10-5 |
3.29×10-5 |
X16 |
保持架磨损失效 |
2×10-4 |
6.59×10-5 |
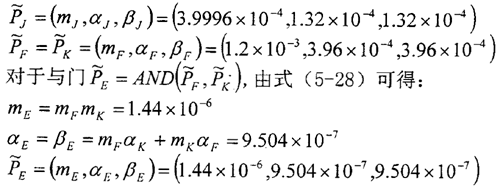
对顶事件T有

它表示与滚柱活齿减速器输出轴不旋转故障概率均值1.15×10-3相差±50%的点的隶属函数为0.1,分布α=β=3.4533×10-4。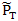 的隶属函数曲线如图5-4所示。 的隶属函数曲线如图5-4所示。

也就是说,在实际情况下,考虑到设计、加工及使用中的各种模糊因素,该减速器的可靠度相对于集合A={R|0.982≤R≤0.994}的隶属度为0.9,而设计要求减速器的可靠度R=0.964,所以该减速器完全可以满足实际工况对减速器的可靠性要求。
5.6 本章小结
1.综合考虑作为串联系统的电动潜油螺杆泵采油系统的可靠性,根据可靠性理论,对采油系统可靠度进行了分配;
2.在分析滚柱活齿减速器组成结构及各种失效可能的基础上,建立了以“输出轴不旋转”为顶事件的减速器故障树。通过定性分析,找出了减速器的全部最小割集,即导致顶事件发生的所有可能方式。给出了减速器中间事件和顶事件的真值函数计算公式;
3.为模拟真实工况下减速器的可靠性情况,在建立的故障树基础上,采用Monte-Carlo 方法随机生成基本事件的故障概率,对减速器进行可靠性数字仿真。通过分析仿真结果,得到各零件的重要度和模式重要度,为改进系统指明了方向;
4.将模糊数学引入滚柱齿减速器的故障树分析中。给出了通过模糊数的运算来表示模糊算子AND和OR的公式,进而得到了顶事件的模糊概率的计算公式。给出了基本事件模糊概率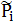 的参照函数为正诚对称型时的计算实例。 的参照函数为正诚对称型时的计算实例。
上一页
下一页
| 









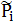 的参照函数为正态对称型且与均值mi相差±50%的点x的隶属度为0.1,则其中各基本事件故障概率的均值mi及计算得到的分布αi和βi如表5-5所示。
的参照函数为正态对称型且与均值mi相差±50%的点x的隶属度为0.1,则其中各基本事件故障概率的均值mi及计算得到的分布αi和βi如表5-5所示。
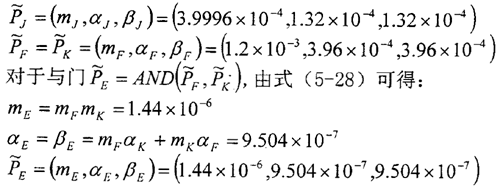

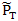 的隶属函数曲线如图5-4所示。
的隶属函数曲线如图5-4所示。