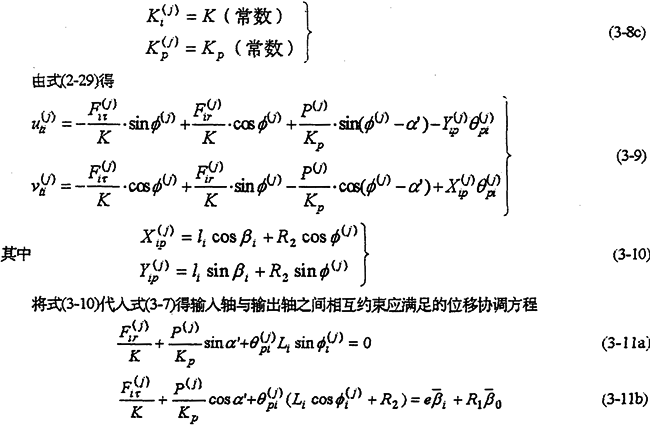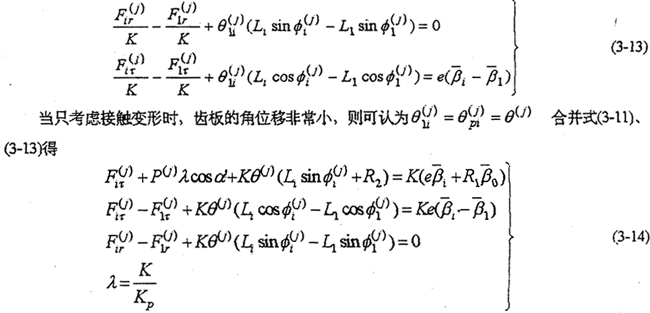内齿行星传动机构动力分析模型的研究

3.1 引言
任何传动装置的设计、制造，都必须首先进行传动机构的运动学及静、动力学的理论分析计算。一般的行星传动机构及少齿差传动机构都有比较成熟的设计计算理论。然而刚推出不久的新型连杆行星齿轮传动一一少齿差内齿行星传动，如三环减速器等，由于其理论分析才刚刚起步，还没有一套完整的分析计算理论，因此，现有的产品在静、动力分析计算上，完全是采用类比法或借助于比较粗糙的理论模型进行设计计算，使得产品性能不稳定，振动噪声严重。本章根据上一章连杆行星齿轮传动机构位移协调原理研究的结果，提出了各种类型的内齿行星传动机构的静、动力分析理论计算模型。利用这些模型，可以从根本上解决该类传动机构的静、动力分析计算问题，为少齿差内齿行星传动装置的设计提供可靠的理论依据。

3.2内齿行星传动机构动力分析基本方程平行轴式少齿差内齿行星传动因其克服机构“死点”的方法不同，其结构形式有所不同。但它们的动力分析模型基本相同。这里以多相并列三轴（三曲柄）式的内齿行星传动机构为例，建立统一的机构动力分析基本方程。为简化分析特作如下假定：
1.机构为匀速转动，即只考虑法向惯性力的作用；
2.由于齿板上的高速轴孔半径r与孔中心距L之比L/r》1，故可以认为偏心套轴承载荷对齿板的作用位置在高速轴孔中心；
3.忽略偏心套、轴、外齿轮等质量较小的构件的重力及惯性力；
4.不计各运动副之间的摩擦阻力；
5.多齿承载各齿对的接触力方向与啮合线平行，且认为其合力在中心啮合齿对上；
6.求解时忽略偏心套半径，即r=0。
由于多相并列内齿行星传动的N片行星齿板结构相同，相邻两片之间的相位差为2Ω/N。因此，在一个周期范围内，各片齿板的受力情况完全一样，故只需分析其中一片齿板即可。齿板及高速轴、输出轴的受力分析如图3-1所示。用动态静力平衡法写出机构的动力分析基本方程为

F^(j)_it、F^(j)_ir是转臂偏心套行星轴承载荷；

P^(j)是行星齿板与输出齿轮的啮合力；

M是高速轴上输入扭矩；
n是输入轴数，n=1为单轴输入，n=2为双轴输入，n=3为三轴输入；
T是输出轴上的负载扭矩；

Q^(j)_z是行星齿板的惯性力；

G^(j)_b是行星齿板的重力；

φ是工况位置角；

φ^(j)_it是行星轴承载荷的方向角；

R₁是输出齿轮的分度圆半径；

R₂是行星齿板的分度圆半径

r是偏心套外圆半径；
L_t是高速轴孔与内齿圈的中心距；

L^(j)_z是行星齿板形心与内齿圈中心的距离；

β_i是高速轴孔相对内齿圈中心的位置角；

β^(j)_z是行星齿板（或连杆）形心相对于内齿圈中心的位置角。

由以上动力分析基本方程不能完全确定内齿行星传动机构的各动载荷值。必须根据第二章的内齿行星传动机构的位移协调条件建立与机构静不定次数相同数目的动力分析补弃方程。
3.3内齿行星传动机构的动力分析补充方程
在第二章中，对内齿行星传动机构的位移协调原理进行了系统的研究。现应用研究的结果建立内齿行星传动机构的动力分析补充方程。
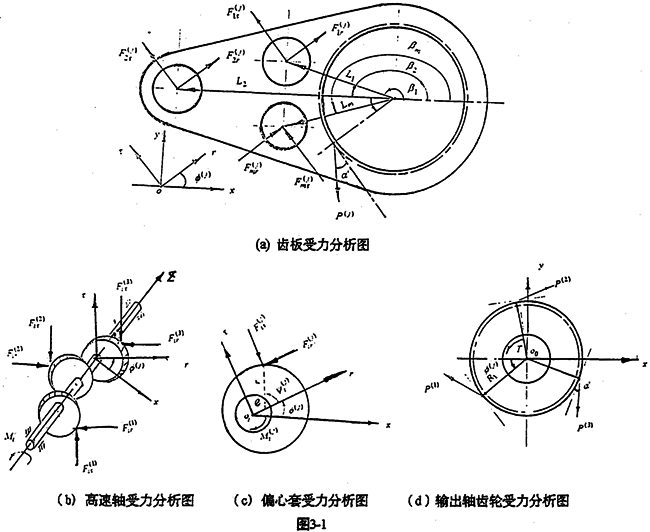
在建立位移协调补充方程时，为便于分析，忽略机构的运动副间隙，并且只考虑偏心套与齿板高速轴孔之间的接触变形，以及齿板与输出齿轮轮齿之间的啮合变形。由式（2-33）、（2-34）及式（2-35）、（2-36）、（2-37）得：

上两式中i=1，2，…，m；j=1，2，…，N
设偏心套与齿板之间的接触变形刚度系数为K^(j)_i，内啮合齿对的变形刚度系数为K^(j)_P，它们除与构件材料和几何结构有关外，还是机构工况位置角φ^(j)的周期函数。各相刚度系数之间的关系为

偏心套与行星齿板之间的接触变形，以夹于二者之间的行星轴承变形为最大，当各高速轴行星轴承型号相同，且只考虑行星轴承变形以及轮齿接触变形时，有

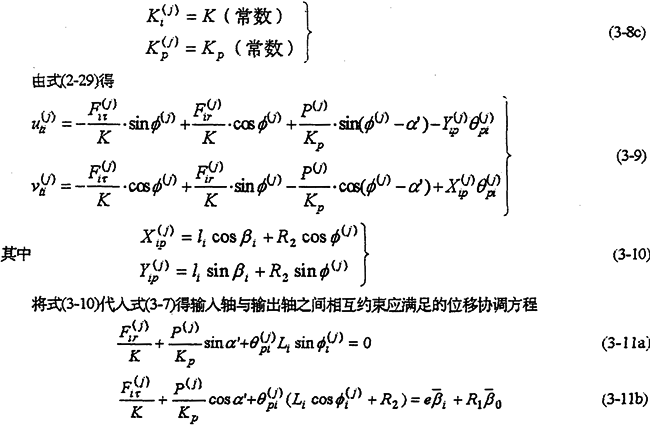
多轴输入时，若忽略分流机构的变形，则各刚性轮子入轴因机构变形引起的转角应相等，即

当分流机构用齿轮传动时，则有

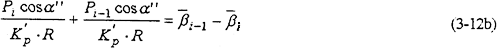
式中P_i是分流齿轮机构轮啮合力；

R是分流齿轮的分度圆半径；
K_P′是轮齿接触刚度；
α″是齿轮啮合角。
同理可推得高速轴之间相互约束的变形协调方程

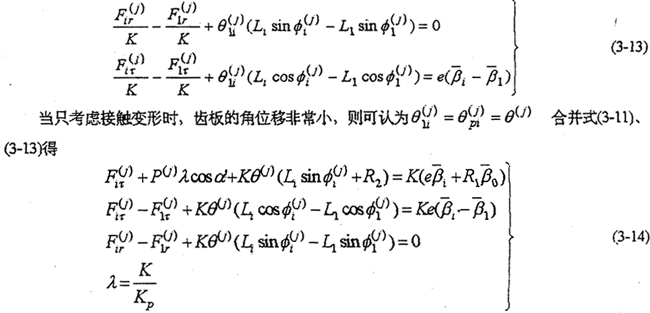
（3-11）及式（3-14）就是少齿差内齿行星传动机的动力分析补充方程。

上一页

下一页