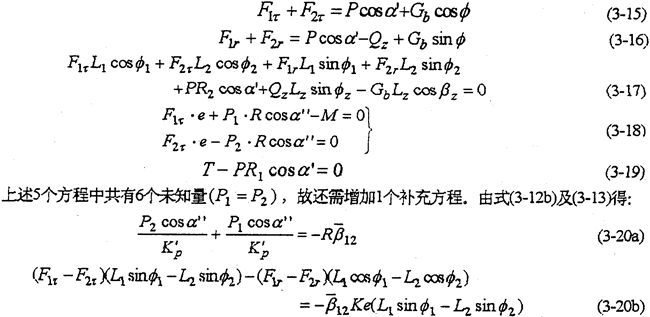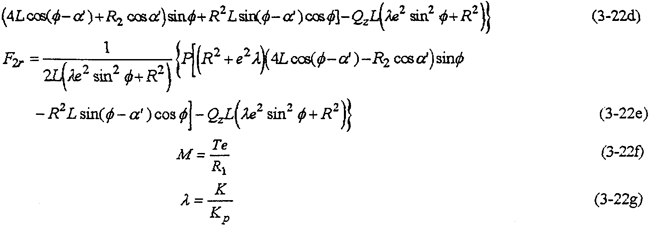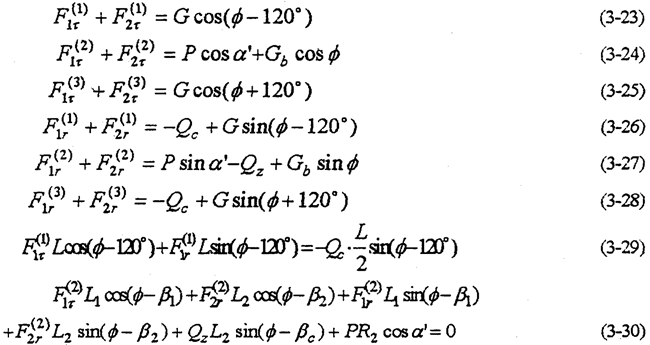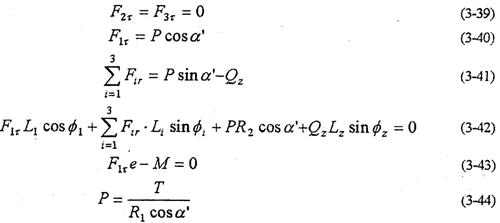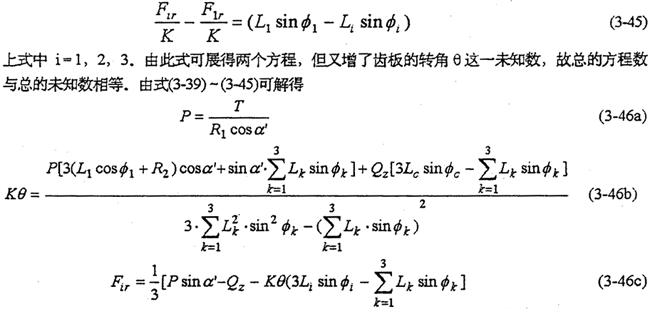3.4一齿环内齿行星传动动力分析模型
一齿环内齿行星传动按机构克服“死点”的方法,有双轴式双轴输入、双轴式单轴输入、以入多轴式等结构形式。
3.4.1双轴式双轴输入一齿环内齿行星传动
这种输入形式是通过一套定轴传动机构将动力分流,传递到两根高速轴上,形成双轴输入。具体结构见图1-6及图3-2。由动力分析基本方程式(3-1)~(3-5)令m=2,N=1得
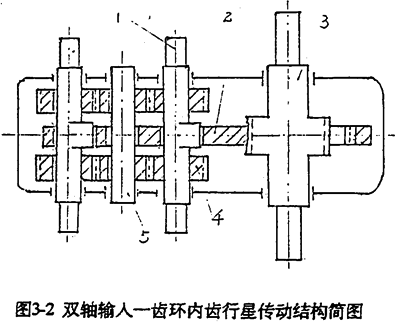
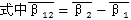
由方程式(3-15)~(3-19)和(3-20)可以完全确定双轴输入式的一齿环内齿行星传动机构的动力参数。各动力参数中除啮合力只与负载大小有关外,其余载荷均与传动机构的几何参数L1,L2,β1,β2,R1,R2,α′,α″等因素有关。故可以通过调整这些参数,以达到满足结构、载荷要求。
当β1=π,β2=0,L1=L2=L时,为高速轴对称于输出轴两则布置,若不计各构件重力,则解为


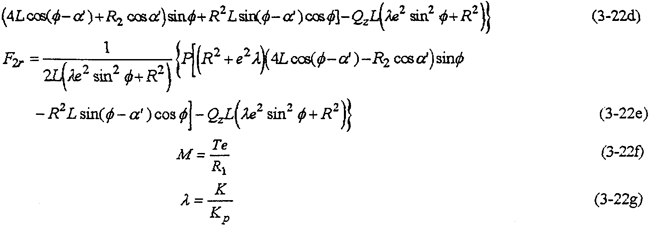
由以上两种情况的解式(3-21)及式(3-22)可知,内齿行星传动机构的行星轴承载荷与轴承接触刚度K及分流机构齿轮的接触刚度Kp有关。分流机构既传递动力又传递运动,使机构在任何时候都具有确定的运动,没有机构的死点位置,这从各解的结果可以看看无论φ怎么变,各载荷值均不会出现无穷大情况。
3.4.2多相并列双曲柄机构一齿环内齿行星传动
以三相并列双曲柄机构一齿环内齿行星传动机构为例(见图1-3图3-3),带行星齿板的双曲柄机构与另外两套双曲柄机构相位差互为120°。疫带行星齿板转动的相位角为φ,则另两相双曲本机构的相位角为φ-120°及φ+120°由动力分析基本方程,取P(1)=P(3)=0,P(j)=P得



3.4.3多轴式一齿环内齿行星传动
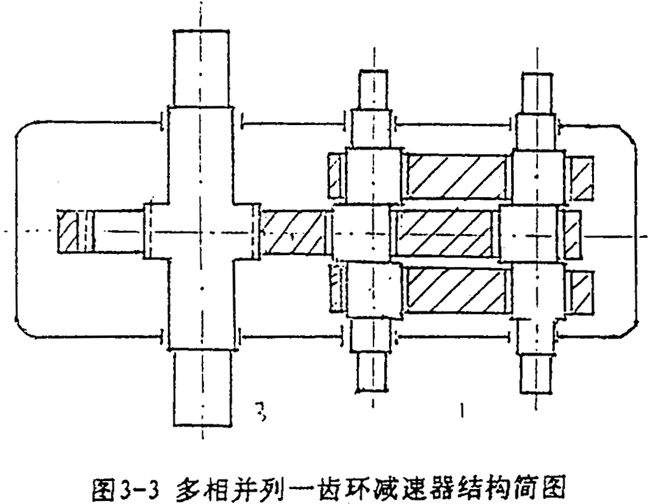
多轴式一齿环内齿行星传动机构是在行星齿板平内采用三根或者三根以上不在同一直线上分布的高速偏心轴(曲柄),支承内齿行星轮(齿板)。当任意二个偏心轴与齿板组成的双曲柄机构,绝对不会处于运动不确定的死点伴置,当它们一起运动时,相互推动,整个机构就不会出现运动不确定的位置。这类内齿行星传动机构见图1-9,图1-10所示等多轴机构的结构形式。除输入轴曲柄有未知输入力矩M外,其余曲柄均认为是二力构件。以三轴式机构为例,由动力分析基本方程,令m=3,N=1得
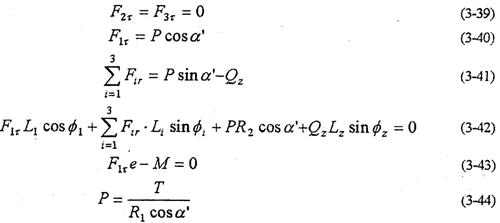
该机构的静不定次数S=1,故需增加一个补充方程,才能完全确定机构的各动力参数。由齿板位移协调方程式(3-14)得
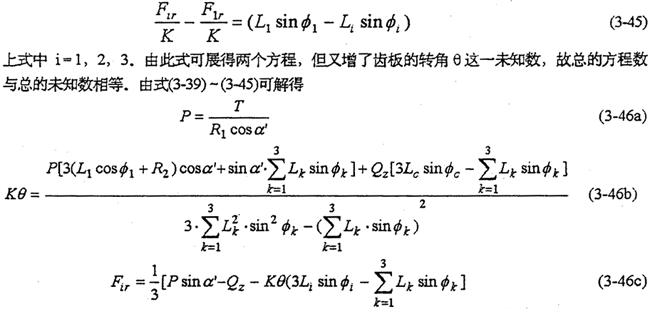

上一页
下一页