为了将理论分析的结果与振动测试分析结果对比印证,将测点选在三个箱体轴承座及齿板支承轴孔的上边缘,如图6-11所示。
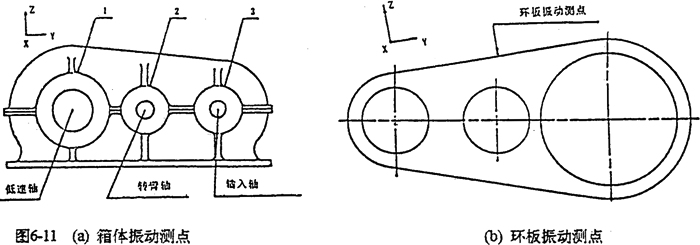
6.4.3实验步骤
1.跑合试验
正式试验之间,减速器在试验台上分别以200rpm,300rpm,400rpm,500rpm,…1500rpm空转,进行20小时的跑合试验,跑合完毕后更换润滑油。
2.空载试验
分别在转速为800rpm,1000rpm,1500rpm三种空载工况下,测试记录SHQ40齿板及箱体轴承座上各测点的振动速度及加速度。
3.加载试验
分别在800rpm,1000rpm,1500rpm等转速下,测试齿板及箱体轴承座的振动速度及加速度。
6.5 理论计算与实验结果对比分析
测试结果经频谱分析处理后,将其与理论计算的结果进行对比分析如下。
1.齿板的振动
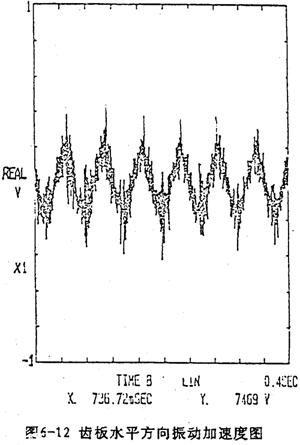
图6-12是齿板的实测振动加速度时域曲线图。从时域曲线图可知,SHQ40型齿板的振动加速度中,存在稳态正弦分量,它是由于齿板作圆周平动运动产生。在其上迭加的每转两次冲击及其振动响应衰减信号,明显表现出齿板的加速度冲击信号,而且最大冲击发生在齿板过死点位置,每转两次非等幅冲击,恰好构成转频16.667Hz的周期函数。
经转换计算后,加速度的最大冲击值为amax二21844mm/s2。从加速度时或曲线规律发生死点的位置以及最大冲击值看均与理论计算结果(见图6-3)相吻合。
2.箱体轴承座的振动
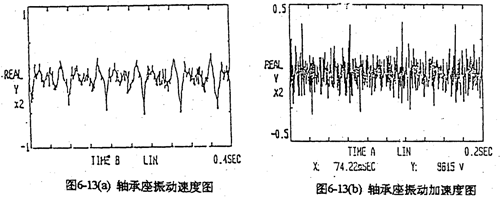
由于每片齿板都存在同样的周期性激励冲击函数,相位差120°,迭加后的总效果仍然是转频周期函数。因此对箱体轴承座的冲击也呈周期性。图6-13是支承轴箱体轴承座的振动速度及加速度的实测时域曲线图。其曲线图的变化规律及幅值与图6-4完全接近。速度及速度冲击值为v
xmax=15.09mm/s,α
max=24960mm/s
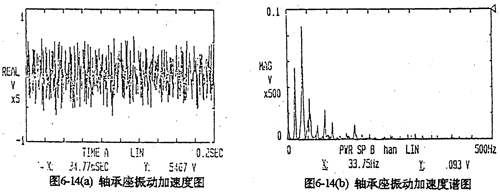
2。图6-14是输入轴轴承座的实测振动加速度时域曲线及其频谱分析图。从加速度谱图中看出,第一谱峰的频率值为33.75Hz,恰好是输入轴转频的二倍,也是死点冲击频率。死点冲击是一周两次,其频率为33.4Hz,这说明理论计算的结果完全可靠;第二谱峰的频率值为16.87Hz,与齿板转频(输入轴频率)相近,是齿板的稳态振动频率;第三谱峰的频率值为49.55Hz,是三环减速器的啮合频率(50Hz),第四谱峰的频率值为99.50Hz,是死点的啮合冲击频率。图6-15是某单齿环内齿行星齿轮减速器的轴承座振动加速度的实测及理论计算曲线图。从图可以看出理论和测试的分布规律极为相似。图中一个周期有一次较大的加速度冲击峰,是由于行星齿板过180°死点时产生的啮合冲击。
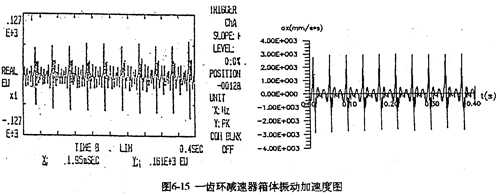
从以上对轴承座的振动实测结果及频谱分析可知,激励三环减速器振动的载荷主要有:
(1)平面四杆机构因变形或误差,在过死点位置时对轴承座产生的冲击载荷;
(2)齿板作平动圆周运动时产生的稳态动载荷;
(3)齿板与外齿轮之间齿轮副的啮合冲击;
(4)平面四杆机构在死点位置时外齿轮造成的冲击载荷。
3.输出转速转动比
由于机构的变形及误差等原因,将使输出转速及传动比动变化,冲击箱体、产生振动。图6-16是对SHLEO15型三环减速器实测及理论计算的转速和传动比随时间变化的波动曲线。输出转速对比为
| |
实测结果 |
理论结果 |
| 最大转速 |
39.184(rpm) |
39.95754(rpm) |
| 最小转速 |
35.358(rpm) |
36.40373(rpm) |
| 波动量 |
3.837 |
3.55381 |
传动比对比为
| |
实测结果 |
理论结果 |
设计传动比 |
17 |
17 |
最大传动比 |
17.556 |
17.580622 |
最小传动比 |
16.229 |
16.017 |
波动量 |
1.327 |
1.5036 |
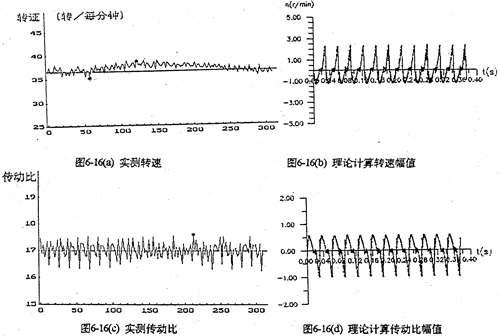
可见,实测值与理论值相近,说明理论计算结果正确。
以上的理论和实验结果都表明,三环减速器的振动源于平行曲柄机构变形或因误差产生的死点冲击。冲击力大小与载荷成正比,冲击发生的时间与转速成反比。功率越大,啮合力也越大,冲击峰越高;转速越高冲击脉宽越小,激振动力带宽越宽。因此,减速器在高速重载时,产生的宽带与较强能量的激振源更容易激发减速器及其附联结沟的广泛共振,从而发生强烈振动。特别是推动环板死点的冲击力矩将可能造成箱体整体及附联结构的强烈振动。冲击力还将引起轴、轴承、键的较大交变动载,并可能引起键联接的松动、摩擦,发热等。
通过对SHQ40型三环减速器的理论计算结果及振动实验的对比研究,说明本文提出的内齿行星传动的动力分析理论完全正确,可以作为三环减速器等内齿行星传动装置的设计分析理论。
6.6控制冲击振动的方案
前面已从理论和实验两方向论证了三环减速器产生振动的根本原因是机构变形及误差引起的死点冲击。因此,应从解决死点冲击出发控制其振动。
1.采用双轴输入降低死点冲击
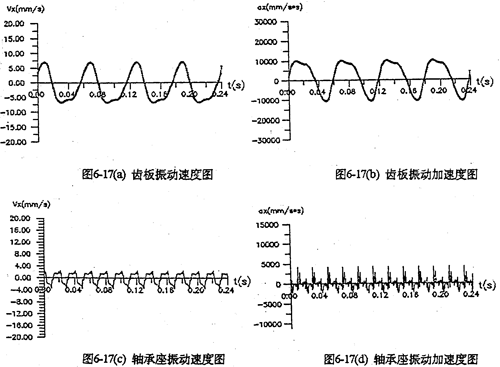
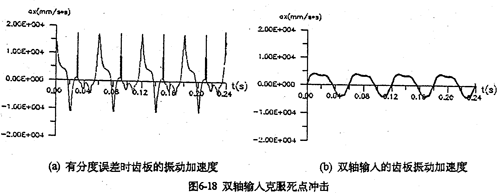
采用双轴输人的齿板及箱体轴承座振动速度、加速度如图6-17所示。从图看出齿板速度及加速度值明显变小(为单轴输人时的0.3倍),而且无冲击,完全属于稳太振动。箱体的振动速度及加速度幅值只是单轴输人时的0.2倍。图6-18a是一轴的偏心套存在0.05度的分度误差时齿板的加速度曲线图,图中明显出现加速度冲击棒线。采用双轴输入后,死点冲击被彻底(见图6-18b) , 变成稳态振动曲线了。因此,为了减小三环减速器的振动,有必要加大三环减速器的横向尺寸,在箱体内增加一套双轴输入的齿轮功率分流机构,或者在箱体外另设计一套功率分流机构,以解决机构过死点的振动问题。
2.改变支承轴的位置
在上一章已经分析过,当三轴水平布置而且高速轴在输出轴的同侧时,载荷幅值最大,各相啮合力等都很不均衡(见图5-24)。图6-19是将支承轴布置在输入轴与输出轴间的150°位置时齿板的振动加速度。由图可知,因误差引起的冲击已被完全克服,而且原有的稳态幅值也降低了很多。
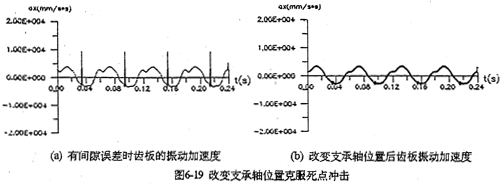
3.增加行星轴承刚度、降低内齿圈刚度
增大行星轴承刚度的目的在于减小双曲柄机构的变形,降低死点冲击幅值。并且使各相啮合力均衡化、减小啮合冲击。图6-20是分别将行星轴承刚度增加一个数量级和内齿圈降低一个数量级时齿板的振动加速度。两者加速度幅值均降低了1/4倍左右。
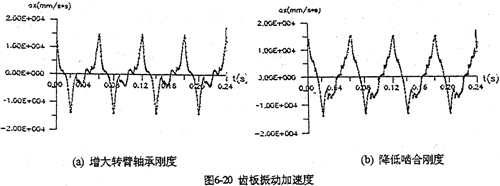
4.减小支承轴或输出轴的箱体轴承刚度
降低箱体轴承刚度是为了吸收内部机构对箱体的冲击振动,减小冲击幅值。图6-21是转速为1500(rpm)即时分别将支承轴及输出轴的箱体轴承与轴之间加一3mm的弹性垫圈时,计算出的箱体振动加速度曲线。从图中看出,减小支承轴箱体轴承刚度比减小输出轴箱体轴承的效果更明显。
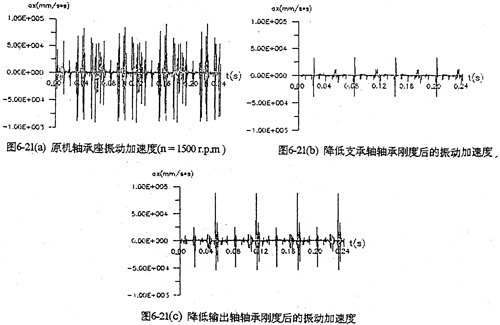
5.增加高速轴的刚度
增加高速轴的刚度是降低冲击载荷的重要途径。轴的刚度大(值径大),扭转、弯曲变形小,双曲柄机构变形也就小,这样既减小了冲击振动、又增加了轴的强度。图6-22将高速轴的直径由原来的45mm加到55mm后的,振动加速度图。
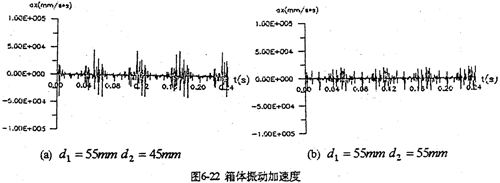
6.对各齿板的死点位置进行修形
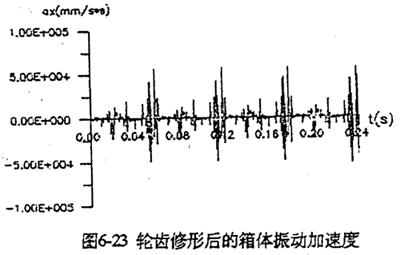
由于机构过死点时,因变形要引起死点冲击,可以通过死点位置及其附近的轮齿(齿板)进行修形,使三相载荷均衡化。图6-23是将死点位置轮齿修形后,轴承座的振动加速度图。与图6-21(a)比较,总体幅值明显下降。
结论
本文对连杆行星齿轮传动过约束机构的位移协调原理从构件到系统,进行了深入的研究,提出了适合于各种类型的连杆行星齿轮传动机构的位移协调条件,并建立其动力分析模型,在此基础上对多次静不定的过约束机构——三环减速器,建立了包括各种因素在内的动力分析模型,对其动力特性、轴间布置以及振动等问题进行了全面的研究,取得了一系列的成果。
综合本文的研究成果,其创造性的研究工作体现在以下几个方面:
●对机构的静不定次数进行了研究,提出了计算过约束机构静不定次数的方法。
●研究了机构构件、组合构件的位移协调原理。从系统观点出发,提出了包括间隙误差在内的连杆行星齿轮传动机构的位移协调原理。圆满地解决了三环减速器等内齿行星传动过约束机构的动力分析问题。
●提出了一齿环、二齿环、多齿环等内齿行星传动机构的结构形式。建立了只考虑接触变形时,在单轴、双轴及多轴输入情况下,这些传动的各种动力分析数学模型,并对常见结构形式的内齿行星齿轮传动给出了啮合力、行星轴承载荷等求解的结果,为内齿行星传动的动力分析计算提供了正确的理论计算公式。
●建立了考虑运动副间隙的内齿行星传动机构的动力分析模型。
●用有限元的单位载荷法对行星齿板、偏心套进行变形分析,求取其整体变形柔度系数,为内齿行星传动机构的动力分析准备可靠数据。
●提出了三环减速器的动力分析精确模型,分析了SHQ40型三环减速器的啮合力、行星轴承载荷、箱体轴承载荷的分布规律。
●研究了影响三环减速器动力特性的各种因素,详细讨论了三环减速器的轴间布置对载荷分布的影响,为改进及优化设计,降低其振动指明了方向。
●从理论上分析了三环减速器产生振动冲击的机理,提出了描述三环减速器振动的速度、加速度,轴间冲击角速度、冲击角加速度,以及输出转速、传动比、输入扭矩等参数的波动函数。并分析了SHQ40 型三环减速器的振动冲击特征。
●用实验研究的结果验证了理论分析结果的正确性,说明本文提出的理论是完全正确的。
●为降低三环减速器振动冲击提出了许多可行方案,并从理论上分析了降低振动冲击的效果。带误差、间隙过约束机构的受力分析研究是一个几乎还没有人涉及的领域。本文针对含有运动副间隙、构件加工误差,且具有多次静不定的过约束机构——连杆行星齿轮传动机构,考虑机 构构件、组合构件以及机构系统的位移协调条件,推导了机构动力分析方程。利用该动力分析方程研究了三环减速器的动力特性,其结果与试验研究的结果相吻合,说明该理论是完全正确的。
上一页













