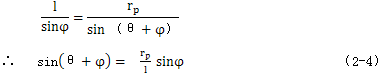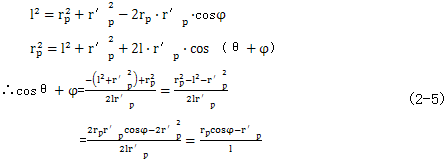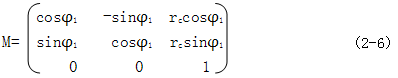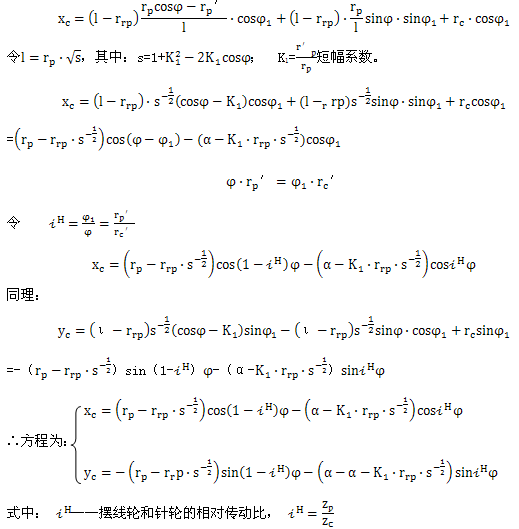2 平行轴少齿差行星传动原理及齿形优化
2.1 引言
行星齿轮传动最基本的形式是2K-H型,如图2-1所示,其传动比为:

由公式(2-1)可知,在径向尺寸受到一定的限制时,要获得较大的传动比,必须减少中心轮Za的齿数。但Za受到最小根切齿数的限制,不能太小。因此,为了独得较大的传动比,人们把行星轮加大,甚至完全去掉中心轮,于是演变出行星齿轮传动的另一种形式:K-H-V行星齿轮传动,其结构图见2-2所示。它的基本构件中心轮b、转臂H和构件V,当中心轮固定,转臂为主动,构件V从动时,传动比为:

中心轮齿数与行星轮齿数之差越小,传动比就越大,把这种传动形式的行星传动称为少齿差行星齿轮传动,常简称少齿差传动。由于行星轮既作公转又自转,因此,要实现定轴输出,还必须一个等角速比机构的输出机构,称之为“W机构”。

图2-1 2K-H型行星齿轮传动

图2-2 K-H-V行星齿轮传动
这两种结构并没有本质的区别,只是选择不同的机构作输出构件和机架,由此可见,少齿差行星齿轮传动机构的实质是由周转轮系与输出机构或输入机构组合而成的齿轮连杆机构,由于行星轮作平面运动,所以一般使由平面四连杆机构构成输出或输入机构。把输出轴作为机架,行星轮作为连杆形成一四杆机构实现运动输出,则所求的四杆机构必须满足以下要求:
1)由于输出的轴作圆周运动,故四杆机构存在曲柄;
2)连杆即行星轮,在机构导引下作圆周平动。
2.2 平行轴摆线针轮行星传动原理与机构形式
2.2.1 平行轴摆线针轮减速器的结构

图2.3 平行轴摆线针轮减速器的结构图
1—箱体,2、4、11、14、22—轴承,3、15—高速轴,5、18—环板,6、10、13、17、21、25—端盖,7—针齿,8—滚动套,9—低速轴,7、10、20—摆线轮,16—螺针,19、24—小齿轮,23—过桥齿轮。
图2.3是本实用新型的实施结构图之一。下面结合附图予以说明:箱体由箱盖和箱座构成,两根高速轴3、15和一根低速轴9的两端由轴承4、14和11支撑在箱座的轴承孔内,轴承外侧装有端盖和密封圈;同一根高速轴上有两个相位差成180°的偏心轴颈,偏心轴颈相当于曲柄机构,其中环板起连杆的作用;环板内孔的圆周上均布着针齿销7,针齿销外有滚动套8;当两块环板5、18上针齿销与固联在低速轴上且相应相位差成180°的两个摆线齿轮12、20啮合时,体内的两根高速轴固联相同的小齿轮119、24,在低速轴上空套一个过桥的大齿轮23,两对外啮合驱动双曲柄顺利通过死点。
2.2.2 传动的原理
平行轴摆线针轮的基本原理是K-H少齿差行星齿轮传动原理,见图2.4,它应用2.1中结构形式,将平行双曲柄四杆机构的曲柄,α是连杆内齿轮,b是定轴输出外齿轮。其传动比为:

2.2.3 传动装置的结构形式
在这个产行四边形机构运动过程中,当两曲柄与连杆共线时,在原曲柄转向不变的条件下,从动曲柄会出现转动方向不确定的现象,曲柄这时所处的位置称为死点位置。
本研究在一个传动装置中采用两个成一定相位差的平行双曲柄四杆机构,它们的连杆内齿轮与两个摆线轮相啮合的情况。为了实现静力平衡,两个平行双曲柄四杆机构的相位差设计为π,结构型式见图2.5。
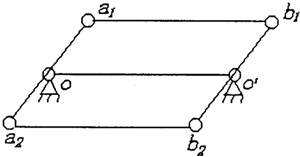
图2.5 相位差π的平行双曲柄四杆机构
采用图2.5的结构尽管实现了静平衡,但仍存在转针方向不确定的问题。本文为解决此问题,提出了三种解决方案。
(1)加连杆
见图2.6。当二块环板处于死点位置时,连杆不在死点位置,即连杆与曲柄有一定的相位角,连杆带动板越过死点位置。
(2)加惰轮机构
见图2.7。轮1和轮3通过键与轴相连,齿轮2空套在轴上。Z1=Z3<Z2,因此ω1=ω3,齿轮不致产生干涉。
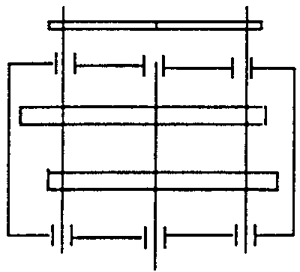
图2.6 加连杆
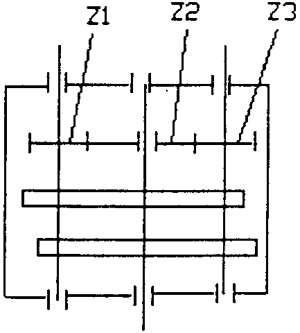
图2.7 加惰轮
(3)加皮带轮
见图2.8。
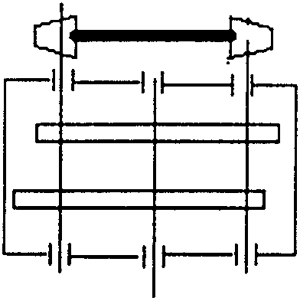
图2.8 加皮带轮
2.3 摆线针轮传动的啮合原理及齿形方程
2.3.1 摆线轮的标准齿形方程
建立如图2.9的标架系:
xoy—绝对坐标系。
xclcyc—固定在摆线轮上的坐标系。
xpopyp—固定针轮上的坐标系。
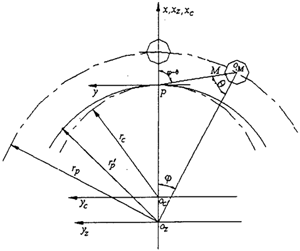
图2.9 标架关系
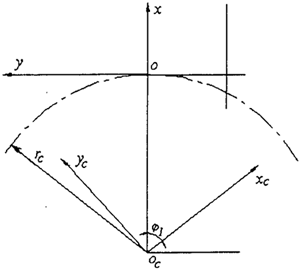
图2.10 啮合关系
建立图2.10的啮合关系,当针轮转过φ角,摆线轮转过φ1角,此时啮合点是M点。根据啮合原理[24],可推导出齿面方程。
令OMP=l,M坐标为M(x,y),

在△ОMPОP中,根据正弦定理有:
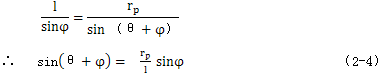
根据余弦定理有:
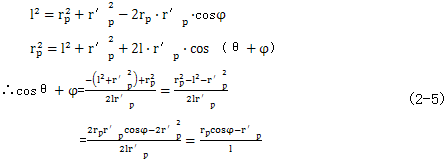
根据坐标间的关系有:

其中:
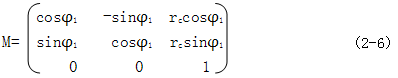
即有:

把(2-3)、(2-4)、(2-5)代入式(2-7)中得:
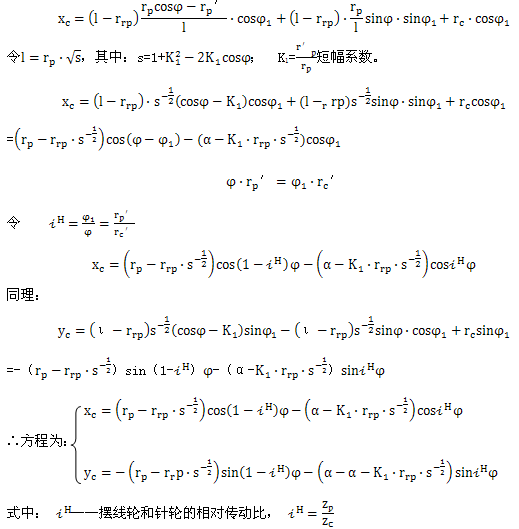
α——偏心距,α=r′P- r′c
φ——转臂相对某一针齿中心矢径的转角
rrp——针齿套外圆半径(mm)
2.3.2 摆线轮的通用齿形方程式
实际应用摆线针轮传动时,为补偿制造误差,便于装拆和保证润滑,摆线轮齿与针齿之是必须有啮合侧隙。因此,实际的摆线轮不能采用标准齿形,都必须修形。
根据摆线针轮传动的啮合与展成法切削加工原理,摆线轮的齿形以下三种基本修形方法,即移距修形法、等距修形法及转角修形法。

由(2-8)可知,摆线轮的实际齿形决定于rp,α,rrp,Zp,△rp,△rrp,δ这七个独立参数。
2.4 两齿差摆线轮的齿顶修形
传动比i≤17,特别i≤11的摆线针轮传动采用传统的“一齿差”齿形时,理论上同时啮合齿数本来就不多,为了形成必要的啮合间隙以补偿制造安装误差和满足润滑要求,摆线轮经过等距或移距修形后,则同时啮合传力的齿数就会更少,从而使承载能力降低,并容易产生胶合。为了克服“一齿差”在小传动比时的弱点,本研究采用两齿差摆线针轮传动,如图2.11所示。由于齿顶尖点使齿廓顶部强度不足,还会在传动中引起噪声,因此需要对齿顶修形[23,27]。
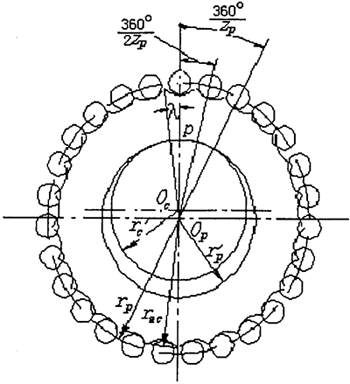
图2.11 两齿差摆线针轮
2.4.1 未修顶前齿顶圆的计算
在上图中,两条短幅外摆线等距曲线的交点构成了二齿差摆线轮的齿顶。

设点A坐标为(xa,ya),则:

由通用摆线轮齿形方程式可得出A点的坐标。
已知rp,rrp,a,Zp=Zp′/2,△rp,△rrp,δ,由式(2-9)算得λ值,再求出φA,xA,yA。那么未修形前齿顶圆的半径rac即可由下式求得:

2.4.2 修顶曲线参数的选择
为了便于在展成法摆线磨齿机上完成修形,本文采用一条短幅外摆线的等距曲线来修形齿顶。
1)目标函数
为使修顶曲线与工作齿廓相连处较光滑地过度,把优选修顶曲线与工作齿廓曲线交点处两切矢的夹角的极小值作为目标函数。
2)结束条件
(1)修顶曲线不得产生顶切,其约束条件为:
g1(x)=rrp2-|ρ0|min<0
式中,|ρ0|min为修顶短幅外摆线等距曲线理论齿廓的最小曲率半径。
(2)修顶曲线的起始点K应保证有足够的同时啮合传力的齿数,通常设计时有4~5个齿轮同时啮合,设对应于啮合点最远的针齿相对于转臂的转角(啮合相位角)为φG,而摆线轮工作齿廓与修顶曲线交点K处的啮合角为φK,可写为如下的结束条件:
g2(x)=φG-φK<0
(3)在修顶起始起点K以前,两齿差传动摆线轮的工作齿廓MK不得与修顶曲线相交,以保证工作齿廓MK的正确齿形,此点可写成约束条件:
g3(x)=x(y)-x2(y)<0
式中x(y),x2(y):分别为对应相同y坐标的工作齿廓的X坐标和修顶曲线的X坐标。
此外,为在展成法磨齿机上一次修完所有齿顶,修顶短幅外摆线的等距曲线参数摆线齿数ZC2通常选为两齿差摆线轮实际齿数ZC′的2倍或3倍。修顶曲线的偏心距a2应符合摆线磨齿机的偏心距系列,通常为0.75,1.0,1.25,1.5等。为使磨齿砂轮有合理寿命,修顶曲线参数中的针齿半径rrp2不应过小,3~5mm<rrp2<rrp/2。
根据上述的目标函数和约束条件,用牛顿迭代法进行优化,其程序框图见2.12。
举例:
已知参数如下:
| rp(mm) |
a(mm) |
rrp(mm) |
Zp |
ZP' |
△rp(mm) |
△rrp(mm) |
δ |
| 109 |
4 |
8.5 |
18 |
36 |
0.60544 |
-0.4554 |
0 |
优化后的修顶曲线的参数为:
| rp2(mm) |
a2(mm) |
rrp2(mm) |
Zp2 |
rac2(mm) |
| 103.13 |
0.75 |
3 |
102 |
105.88 |

图2.12 二齿差摆线轮齿形修形的优化框图
上一页
下一页